2022
TRANSFORMADA DE LAPLACE
APLICACIONES DE LA TRNSFORMADA DE LAPLACE
VICTOR BUSTAMANTE
INTRODUCCIÓN
La transformada de Laplace ha sido en los últimos años de gran importancia en los
estudios de ingeniería, matemática, física, entre otras áreas científicas, ya que
además de ser de gran interés en lo teórico, proporciona una forma sencilla de
resolver ecuaciones diferenciales, transformándolas en ecuaciones algebraicas.
Originalmente la transformada de Laplace fue presentada por Pierre-Simon
Laplace (1745-1827) en su estudio sobre la teoría de la probabilidad, y en principio
fue tratada como un objeto matemático de interés meramente teórico.
Las aplicaciones actuales surgen cuando diversos matemáticos trataron de dar una
justificación formal a las “reglas operacionales” usadas por Oliver Heaviside
(1850-1925) en el estudio de ecuaciones de la teoría electromagnética.
DEFINICIÓN
Sea f una función definida para t ≥ 0. La transformada de Laplace se define como
sigue:
∝
𝐿{𝑓 (𝑡 )} = ∫ 𝑒 −𝑠𝑡 𝑓(𝑡 )𝑑𝑡
0
Se dice que la transformada de Laplace existe si la integral anterior converge, en
caso contrario se dice que la transformada de Laplace no existe.
Por lo general, para denotar la función que se desea trasformar se usan letras
minúsculas y la letra mayúscula corresponde a su transformada. De esta manera
tendremos:
𝐿{𝑓(𝑡 )} = 𝐹 (𝑠),
𝐿{𝑔(𝑡 )} = 𝐺 (𝑠),
𝐿{𝑦(𝑡 )} = 𝑌(𝑠)
PIERRE-SIMON LAPLACE
(Pierre-Simon, marqués de
Laplace;
Beaumont-enAuge, Francia, 1749 - París,
1827) Matemático francés.
Hijo de un granjero, inició
sus estudios primarios en la
escuela local, pero gracias a
la
intervención
de D'Alembert, quien había
quedado
profundamente
impresionado por un escrito
del joven sobre los principios
de la mecánica, pudo
trasladarse a la capital, donde
consiguió una plaza en la École Militaire. Entre 1771 y 1789 desarrolló la mayor
parte de su trabajo sobre astronomía, particularmente su estudio sobre las
desigualdades planetarias, seguido por algunos escritos sobre cálculo integral y
ecuaciones diferenciales en derivadas parciales. Destaca entre su producción del
período 1784-1787 la determinación de la atracción de un esferoide sobre una
partícula situada en su exterior, para cuya determinación introduciría el análisis de
armónicos o coeficientes de Laplace y el concepto de potencial.
En 1796 publicó su Exposición del sistema del mundo, en el que ofreció una
versión divulgativa de las leyes de Newton y una exposición del sistema solar;
como explicación de su origen, la obra proponía la hipótesis nebular, mejor
perfilada anteriormente por Immanuel Kant. Sus resultados analíticos sobre la
mecánica estelar se publicaron en los cinco volúmenes del Tratado de mecánica
celeste (1799-1825). En los dos primeros volúmenes describió métodos para el
cálculo del movimiento de los planetas y sus satélites, y determinó sus trayectorias.
El tercero contiene la aplicación de estos métodos y muchas tablas astronómicas.
En 1814, Laplace publicó un ensayo sobre probabilidades orientado al lector
profano, que le serviría de base para la segunda introducción de su Teoría analítica
de las probabilidades (tratado publicado en 1812), donde incluyó una exposición
del método de los mínimos cuadrados, base de toda la teoría de los errores.
Honrado por Napoleón, que en 1806 lo hizo conde, desde ese mismo año impulsó
junto con Claude Louis Berthollet la Sociedad de Arcueil, que se convertiría en un
influyente círculo científico.
EJERCICIO 01:
Usando transformadas de Laplace calcule la deflexión de una viga de acero con
una longitud de 4 𝑚𝑡. Dicha viga trabajara con un monorriel y soportara una carga
máxima total de 500 𝑘𝑔 . sabiendo que: 𝐼 = 210000𝑀𝑝𝑎, 𝐸 = 2,64 ∗ 10 − 6
I
E
L
F
M
RA
RB
X
Y
∑ 𝐹𝑌
Momento de inercia
Módulo de elasticidad del acero
Longitud total
Fuerza
Momento de fuerza
Reacción en a
Reacción en b
Distancia
Deflexión
Sumatoria de fuerza en y
C
L
𝐿−1
constante
Transformada de Laplace
Transformada inversa de Laplace
Calculando las reacciones en los apoyos
∑ 𝑀𝐴 = 0
∑ 𝐹𝑦 = 0
𝑅𝐴 = 𝑅𝐵 =
𝐹
2
Realizando un corte antes del apoyo B y haciendo sumatoria de momentos respecto
al corte, tenemos:
∑ 𝑀𝑐𝑜𝑟𝑡𝑒 = 0
𝑀(𝑥) = −𝑅𝐴 𝑥
Determinación de la ecuación de deflexión:
𝑑2 𝑦
Ecuación diferencial básica de una viga :
𝑑𝑥 2
=
𝑀
→ 𝐸𝐼 =
𝐸𝐼
𝑑2 𝑦
𝑑𝑥 2
𝑀
𝐹
Ecuación de momento de una viga simplemente apoyada: 𝑀(𝑥) = −𝑅𝐴 𝑥 = − 𝑥
2
Condiciones iniciales: tomando en cuenta que la
deflexión en los apoyos es cero, tenemos:
𝑦 (0) = 0 𝑦 𝑦 (𝐿 ) = 0
Haciendo uso de la ecuación diferencial para la deflexión
2
𝐸𝐼 {
de una viga y Sustituyendo en el modelo
𝑑 𝑦
= −𝐹
𝑥
2
2}
𝑑𝑥
de la ecuación para el momento:
2
Aplicando transformada de Laplace en ambos lados
de la ecuación:
𝐸𝐼𝐿 {
𝑑 𝑦
2
𝑑𝑥
} = 𝐿{
−𝐹
𝑥}
2
𝐸𝐼{𝑠2 𝐿(𝑦) − 𝑠𝑦(0) − 𝑦´ (0)} = [
Aplicando la ecuación diferencial
de la transformada de una derivada
nos queda:
−𝐹
]
2𝑠2
𝐸𝐼{𝑠2 𝐿(𝑦) − 𝐶} = [
−𝐹
Aplicando la transformada inversa de Laplace: 𝐿{𝑦} =
(propiedad producto constante)
−𝐹
Aplicando y(L)=0
𝑦 (𝐿 ) = [
Sustituyendo C en y(x):
𝑦 (𝑥 ) = [
12𝐼𝐸
[ 2]+𝐶
2𝑆
𝐸𝐼𝑠 2
=
1
[
−𝐹
𝐸𝐼 2𝑠 4
]+
𝑐
𝑠2
𝐿3 ] + 𝐶𝐿 = 0
−𝐹
𝐹∗𝐿2
𝑋2 +
∗ 𝑋]
12∗𝐸∗𝐼
12∗𝐸∗𝐼
𝑦(𝑥) = −𝐹
9.81𝑚
𝐹 = 𝑀 ∗ 𝑔 entonces tenemos 𝐹 = 500𝑘𝑔 ∗ 2 = 4905 𝑁
𝑠
−4900
4900 ∗ 42
2
(
)
[
𝑦 𝑥 =
2 +
∗ 2]
12 ∗ 20.6 ∗ 10−10 ∗ 210000
12 ∗ 20.6 ∗ 102 ∗ 210000
Por lo tanto, encontramos la ecuación de deflexión de una viga simplemente
apoyada.
La deflexión máxima ocurre en I/2 sabiendo que:
I=13mm es lo que se flexiona la viga con una carga puntual, este fenómeno es
conocido como pandeo.
−𝐹
]
2𝑠2
EJERCICIO 02:
Luego que un pastel estuviera en el horno 30 minutos, este alcanzó una temperatura
de 95.5 C, por lo cual, al transcurrir otros 30 minutos en el exterior su temperatura
fue de 55.9 C, considerando que la temperatura de ambiente es de 24.5 C. Calcular
la ecuación del tiempo de enfriamiento del pastel mediante la transformada de
Laplace.
Datos:
𝒅𝑻
= 𝑲(𝑻 − 𝑻𝑨 )
𝒅𝒕
Temperatura después de estar en
el horno 95.5 𝐶
Temperatura de ambiente 24.5 𝐶
𝒅𝑻
= 𝑲𝒅𝒕
(𝑻 − 𝑻𝑨 )
∫
𝒅𝑻
= ∫ 𝑲𝒅𝒕
(𝑻 − 𝑻𝑨 )
𝒍𝒏|𝑻 − 𝑻𝑨 | = 𝑲𝒕 + 𝑪
𝒍𝒏|𝟗𝟓. 𝟓 − 𝟐𝟒. 𝟓| = 𝑲𝒕 + 𝑪
𝑇=0
𝒍𝒏|𝟕𝟏| = 𝑪
𝑪 = 𝟒. 𝟐𝟔𝟑
𝒍𝒏|𝟓𝟓. 𝟗 − 𝟐𝟒. 𝟓| = 𝑲(𝟑𝟎) + 𝑪
𝒍𝒏|𝟑𝟏. 𝟒| = 𝟑𝟎𝑲 + 𝟒. 𝟐𝟔𝟑
𝑲 = −𝟎. 𝟎𝟐𝟕𝟐
Temperatura luego de 30 min
55.9
SOLUCIÓN:
𝒅𝑻
𝒅𝒕
= 𝑲(𝑻𝑨 − 𝑻)
𝒅𝑻
= 𝑲𝑻𝑨 − 𝑲𝑻
𝒅𝒕
𝑳{𝑻´(𝒕) − 𝑲𝑻𝑨 − 𝑲𝑻 = 𝟎}
𝒑𝑻(𝒕) − 𝑻(𝑨) − 𝑲𝑻(𝒕) =
𝑻(𝒕) (𝑷 − 𝒌) =
𝟎. 𝟔𝟔𝟔𝟒
𝒑
𝑇(𝐴) = 95.5 𝐶
𝟎. 𝟔𝟔𝟔𝟒
+ 𝟗𝟓. 𝟓
𝒑
𝑻(𝒕) =
𝟎. 𝟔𝟔𝟔𝟒 + 𝟗𝟓. 𝟓𝒑
𝒑(𝒑 − 𝒌)
𝑻(𝒕) =
𝑨
𝑩
+
𝒑 𝒑−𝑲
𝑳−𝟏 {
𝑇0 . 𝐾 = 0.6664
𝟐𝟒. 𝟓
𝟕𝟏
+
= 𝟎}
𝒑
𝒑 + 𝟎. 𝟎𝟐𝟕𝟐
𝑻(𝒕) = 𝟐𝟒. 𝟓 + 𝟕𝟏𝒆−𝟎.𝟎𝟐𝟕𝟐𝒕
EJERCICIO 03:
𝐾 = −0.0272
Se realiza una neutralización química de HCL con NaOH. Si al inicio hay 4 moles
de HCL y durante la neutralización se observa que a los 5 segundos solo el 30%
de la solución ha reaccionado, calcular:
a) Los moles de la solución después de 10 segundos.
b) El tiempo que se requiere para la neutralización llegue al 50%
𝐻𝐶𝑙(𝑎𝑐) + 𝑁𝑎𝑂𝐻(𝑎𝑐) → 𝑁𝑎𝐶𝑙(𝑎𝑐) + 𝐻2 𝑂(𝑙)
𝑦(0) = 4 𝑚𝑜𝑙𝑒𝑠
30%
) = 1.2 𝑚𝑜𝑙𝑒𝑠 → 4 𝑚𝑜𝑙 − 1.2 𝑚𝑜𝑙 = 2.8 𝑚𝑜𝑙𝑒𝑠
𝑦(5) = 2.8 𝑚𝑜𝑙𝑒𝑠 → 4 (
100%
𝑑𝑦
𝐿 {𝑦 ´ } =
= 𝑘𝑦 → 𝑦: 𝑛𝑢𝑚𝑒𝑟𝑜 𝑑𝑒 𝑚𝑜𝑙𝑒𝑠
𝑑𝑡
𝑦 ´ = 𝑘𝑦 → 𝑆𝑦(𝑠) − 𝑦(0)
𝑦 ´ − 𝑘𝑦 = 0 → 𝑆𝑦(𝑠) − 𝑦(0)
𝐿{𝑦 ´ } = 𝑆𝑦(𝑠) − 4 𝐿{𝐾𝑦 } = 𝐾𝑦(𝑠)
𝑆𝑦(𝑠) − 𝐾𝑦(𝑠) − 4 = 0
𝑦(𝑠) (𝑆 − 𝐾) − 4 = 0
4
1
𝑦(𝑠) =
→ 𝐿−1 =
∴ 𝐿{𝑒 𝑎𝑡 }
(𝑆 − 𝐾)
𝑠−𝑎
𝐴𝑝𝑙𝑖𝑐𝑎𝑚𝑜𝑠 𝑙𝑎 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑎𝑑𝑎 𝑖𝑛𝑣𝑒𝑟𝑠𝑎 𝐿−1
𝑦 = 4𝑒 𝑘𝑡 → 𝑆𝑜𝑙𝑢𝑐𝑖ó𝑛 𝑔𝑒𝑛𝑒𝑟𝑎𝑙
𝑯𝒂𝒍𝒍𝒂𝒏𝒅𝒐 𝒍𝒂 𝒄𝒐𝒏𝒔𝒕𝒂𝒏𝒕𝒆 “𝒌”
2.8 = 4𝑒 𝑘(5)
2.8
= 𝑒 𝑘(5)
4
2.8
ln ( ) = 𝑘(5)
4
−0.356 = 𝑘(5)
−0.356
=𝑘
5
−0.071 = 𝑘
a) Los moles de la solución después de 10 segundos
𝑦 = 4𝑒 −0.071(10)
𝑦 = 1.9665 𝑚𝑜𝑙𝑒𝑠
𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑒𝑙 𝑛ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑚𝑜𝑙𝑒𝑠 𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑒𝑠 𝑒𝑛 𝑙𝑎 𝑠𝑜𝑙𝑢𝑐𝑖ó𝑛 𝑑𝑒𝑠𝑝𝑢é𝑠 𝑑𝑒 10 𝑠𝑒𝑔𝑢𝑛𝑑𝑜𝑠
𝑒𝑠 𝑑𝑒 𝑎𝑝𝑟𝑜𝑥𝑖𝑚𝑎𝑑𝑎𝑚𝑒𝑛𝑡𝑒 1.9665 𝑚𝑜𝑙𝑒𝑠.
b) El tiempo que se necesita para que la neutralización llegue al 50%
2 = 4𝑒 −0.071𝑡
1
= 𝑒 −0.071𝑡
2
1
ln ( ) = −0.071𝑡
2
𝑡 = 9.7626
𝑅𝑒𝑠𝑝𝑢𝑒𝑠𝑡𝑎: 𝑒𝑙 𝑡𝑖𝑒𝑚𝑝𝑜 𝑞𝑢𝑒 𝑠𝑒 𝑟𝑒𝑞𝑢𝑖𝑒𝑟𝑒 𝑝𝑎𝑟𝑎 𝑞𝑢𝑒 𝑙𝑎 𝑛𝑒𝑢𝑡𝑟𝑎𝑙𝑖𝑧𝑎𝑐𝑖ó𝑛 𝑙𝑙𝑒𝑔𝑢𝑒 𝑎𝑙 50%
𝑒𝑠 𝑑𝑒 9.726 𝑠𝑒𝑔𝑢𝑛𝑑𝑜𝑠.
EJERCICIO 04:
Una pequeña bola de cobre a 120°𝑐 se deja caer en un tanque grande lleno de agua
a 10°𝑐. En este caso se transfiere calor de la bola de cobre al agua, haciendo que
la temperatura de la bola empiece a disminuir. El coeficiente de la transferencia de
calor entre la bola y el agua es 0.02, también llamado razón de enfriamiento.
a) Obtener el modelo matemático
b) Hallar la función temperatura respecto al tiempo con la transformada de
Laplace
c) ¿Qué temperatura tendrá el sistema a los 3 min?
d) ¿Cuánto tiempo transcurre (en segundos) para que la temperatura sea de
30°𝑐?
Para el inciso a)
Datos:
𝑇𝑚 = 10°𝑐
𝑇(0) = 120°𝑐
𝑘 = 0.02
Sustituir en la ley de enfriamiento
𝑑𝑇
= −𝑘 (𝑇 − 𝑇𝑚 )
𝑑𝑡
𝑑𝑇
= −(0.02)(𝑇 − 10)
𝑑𝑡
𝑑𝑇
+ (0.02𝑇) = 0.2
𝑑𝑡
Para el inciso b)
Transformar cada termino
𝐿{𝑡 } = 𝐹(𝑠)
𝐿{𝑇 ´ } = 𝑠𝐹 (𝑠) − 𝑇(0) = 𝑠𝐹 (𝑠) − 120
𝐿{0.2} =
0.2
𝑠
Mediante fracciones parciales
120𝑠 + 0.2 𝐴
𝐵
= +
𝑠(𝑠 + 0.02) 𝑠 𝑠 + 0.02
120𝑠 + 0.2 = 𝐴(𝑠 + 0.02) + 𝐵(𝑠)
𝐴 + 𝐵 = 120
Despejando F(s):
𝑠𝐹 (𝑠) − 120 + 0.02𝐹 (𝑠)
0.2
=
𝑠
0.2
𝐹 (𝑠)(𝑠 + 0.002) =
+ 120
𝑠
120𝑠 + 0.2
𝐹 (𝑠 ) =
𝑠(𝑠 + 0.02)
0.02𝐴 = 0.2
𝐴 = 10
𝐵 = 110
10
110
𝐹 (𝑠 ) =
+
𝑠
𝑠 + 0.02
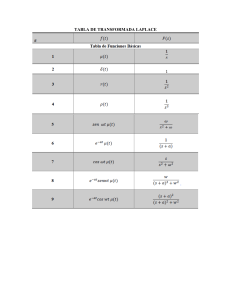
Con el uso de tablas:
1
f(t)
𝟏
3
𝒕𝜶 , −𝟏 < 𝜶
2
f(t)
𝒕 , 𝒏 = 𝟏, 𝟐, 𝟑, 𝟒 …
4
𝒆𝜶𝒕
𝒏
Aplicando T. inversa
1
1
}
𝐿− {𝐹 (𝑠)} = 10𝐿− { } + 110𝐿− {
𝑆
𝑆 + 0.02
𝑇{𝑡 } = 110𝑒 −0.02𝑡 + 10
Gráficamente:
F(s)
𝟏
𝒔
𝝉(𝜶 + 𝟏)
𝒔𝜶+𝟏
F(s)
𝒏!
𝒔𝒏+𝟏
𝟏
𝒔−𝒂
Para inciso c)
Sustituir 𝑡 = 3𝑚𝑖𝑛 (en seg) en T(t)
𝑡 = 3𝑚𝑖𝑛 = 3 ∗ 60𝑠 = 180𝑠
𝑇(180) = 110𝑒 −0.02(180) + 10
𝑇(180) = 13.0006°𝐶
Para el inciso d)
Igualar T(t)=30 y despejar t
30 = 110𝑒 −0.02𝑡 + 10
20
= 𝑒 −0.02𝑡
110
2
11
𝑙𝑛( )
−0.02
=𝑡
𝑡 = 85.24 𝑠
EJERCICIO 05:
Para la red de la figura, encuentre 𝒊(𝒕) para 𝒕 > 𝟎:
Para 𝒕 < 𝟎:
Reduciendo:
Resolviendo:
𝑉 (0) =
Para 𝒕 > 𝟎:
(50𝑉)(5𝛺) 25
=
𝑉
(25 + 5)𝛺
3
Pasando al dominio de Laplace:
50𝑉 →
50
𝑠
1𝐻 → 𝑆𝐿 = 𝑆
1
1
25
𝐹→
=
2𝑆
𝑆𝐶
𝑆
𝑉(0) 25
=
𝑆
3𝑆
CIRCUITO:
Resolviendo:
(4 + 𝑆 +
25
10 25
)𝐼 =
−
𝑆
𝑠
3𝑠
5
5
5
3𝑠
𝐼= 2
=
=
𝑠 + 4𝑠 + 25 3(𝑆 2 + 4𝑆 + 25) 3(𝑆 + 2)2 + 21
𝑠
𝒊(𝒕):
𝑆
1
𝐿−1 { (
)}
2
3 (𝑆 + 2) + (√21)2
𝐿−1 {
𝑆
√21)
(
)}
3√21) (𝑆 + 2)2 + (√21)2
𝑆
𝑖(𝑡) = [
𝑒 −2𝑡 𝑠𝑒𝑛(√21𝑡)] 𝑢(𝑡)𝐴
3√21)
𝑆
𝑖(𝑡) = [
𝑒 −2𝑡 𝑠𝑒𝑛(√21𝑡 − 90)] 𝑢(𝑡)𝐴
3√21)