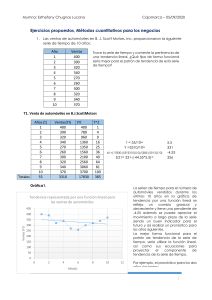
MODELOS ESTADÍSTICOS Suavización Exponencial • Modelo de Suavización Exponencial Simple Es una evolución del método de promedio móvil ponderado. Busca ajustar los pronósticos en dirección opuesta a las desviaciones del pasado mediante una corrección que se ve afectada por un coef. de suavización. Suaviza fluctuaciones en la historia reciente. Ventajas: No necesita gran volumen de datos históricos de demanda. Al ser un modelo exponencial, es más preciso ¿Cuándo usarlo? Para patrones de demanda aleatorios o nivelados donde se pretende eliminar el impacto de elementos irregulares históricos mediante un enfoque en periodos de demanda reciente. suavización tenderá a ser pequeña (0,10 por ejemplo), debido a que, no requerimos un elevado índice de respuesta frente a los cambios entre la demanda real y la demanda pronosticada. Caso contrario es cuando la compañía comienza a tener un crecimiento en su demanda, lo que va a requerir un alfa más elevado (0,30 por ejemplo) para dar mayor importancia a la demanda reciente. • Adaptativo Se usa el Alpha base solo para los primeros 3 periodos y luego se calcula el Alpha en base al Delta. La suavización exponencial simple de respuesta adaptiva es un método que trata de que el valor de la constante de suavización se adapte al cambio que están teniendo los datos. Alpha cambia medida que va cambiando el patrón de los datos de la serie de tiempo. 𝛼𝑡+1 = | ▪ 𝑥̂𝑡 : Pronóstico de ventas en unidades en el periodo t ▪ 𝑥̂𝑡−1 : Pronóstico de ventas en unidades del periodo t-1 ▪ 𝑥𝑡−1 : ventas reales en unidades en el periodo t-1 ▪ 𝛼: coeficiente de suavización (entre 0,0 y 1,0) Alpha suele variar entre 0,05 y 0,5, su variación se hace de acuerdo con la necesidad de darle más peso a datos recientes (Alpha mas elevado) o a datos anteriores (Alpha más bajo). En este sentido, si α=1, nuestro pronóstico de demanda del próximo periodo será exactamente igual al del periodo actual. EJEMPLO: teniendo un producto o servicio con demanda estable a través del año, nuestra constante de 𝐸𝑆𝑡 | 𝐸𝐴𝑆𝑡 Error Suavizado (𝐸𝑆𝑡 ) 𝐸𝑆𝑡 = 𝛽𝐸𝑡 + (1 − 𝛽)𝐸𝑆𝑡−1 Erros Absoluto Suavizado (𝐸𝐴𝑆𝑡 ) 𝐸𝐴𝑆𝑡 = 𝛽|𝐸𝑡 | + (1 − 𝛽)𝐸𝐴𝑆𝑡−1 Error de Pronóstico en el momento t (𝐸𝑡 ) 𝐸𝑡 = 𝑥𝑡 − 𝑥̂𝑡 • Exponencial Doble (Holt-Winters) Con este método se agrega una constante de suavización delta (δ), cuya función es reducir el error que ocurre entre la demanda real y el pronóstico. El método de suavización exponencial con ajuste a la tendencia requiere de dos constantes de suavización: alfa (α) y delta (δ). Su valor puede estar entre 0 y 1, pero a nivel práctico varía entre 0,05 y 0,50. ¿Cómo escoger los valores más adecuados? Los criterios para definir los valores de las constantes son similares al método de suavización simple. Para alfa dependerá de la importancia que otorgamos a datos recientes (alfa α más elevada) o a datos más antiguos (alfa α más bajo). El delta funciona similar. Un δ elevado responde con más velocidad a los cambios en la tendencia, mientras que un δ inferior tiende a suavizar la tendencia actual, dando menos peso a los datos recientes. 𝑆𝑡 = α ∗ 𝑋𝑡−1 + (1 − α) ∗ (𝑆𝑡−1 + 𝐵𝑡−1 ) 𝐵𝑡 = β ∗ (𝑆𝑡 − 𝑆𝑡−1 ) + (1 − β) ∗ 𝐵𝑡−1 𝐹𝑚 = 𝑆𝑇 + 𝑚 ∗ 𝐵𝑇 Donde: ▪ 𝑆𝑡 : Pronóstico suavizado exponencialmente con la serie de datos del periodo t ▪ α: Constante de suavizamiento para el promedio ▪ 𝑋𝑡−1 : Demanda real del periodo anterior ▪ 𝑆𝑡−1 : Pronóstico del periodo anterior ▪ 𝐵𝑡−1 : Tendencia estimada para el periodo anterior ▪ 𝐵𝑡 : Tendencia suavizada para el período t ▪ β: Constante de suavizamiento para la tendencia ▪ 𝑆𝑡−1 : Pronóstico suavizado exponencialmente con la serie de datos del periodo t-1. ▪ 𝐹𝑚 : Pronóstico de demanda con tendencia. segunda a la serie atenuada obtenida mediante la primera atenuación. 𝑆′𝑡 = α ∗ 𝑋𝑡 + (1 − α) ∗ (𝑆′𝑡−1 ) 𝑆′′𝑡 = α ∗ 𝑆′𝑡 + (1 − α) ∗ (𝑆′′𝑡−1 ) 𝑎 = 2 * 𝑆′𝑡 − 𝑆 ′′ 𝑡 α b= ∗ ( 𝑆′𝑡 − 𝑆 ′′ 𝑡 ) 1−α 𝐹𝑚 = a + m ∗ b Donde: ▪ 𝑋𝑡 : Ventas reales del periodo t ▪ 𝑆′𝑡 : Valor suavizado exponencialmente de Xt en el periodo t. ▪ 𝑆′′𝑡 : Valor doblemente suavizado exponencialmente de Xt en el periodo t ▪ 𝑎: Similar a la medición de la intersección de la ordenada con una recta que cambia durante la serie de tiempo. ▪ b: Similar a la medición de la pendiente de una recta que cambia durante la serie de tiempo. ▪ 𝐹𝑚 : Pronóstico ▪ α: constante de suavización. ▪ m: periodos a pronosticar en el futuro. • • Método de Brown. ¿Cuándo usarlo? Este modelo es apropiado para series en las que hay una tendencia lineal y sin estacionalidad. Sus parámetros de suavizado son el nivel y la tendencia, que se supone que son iguales. El modelo de Brown es, por tanto, un caso especial del modelo de Holt. El suavizado exponencial de Brown es más parecido a un modelo ARIMA con cero órdenes de auto regresión, dos órdenes de diferenciación, y dos órdenes de media móvil, con el coeficiente para el segundo orden de media móvil igual al cuadrado de la mitad del coeficiente para el primer pedido. Este método consiste en realizar dos suavizaciones exponenciales, a partir de las cuales se obtendrá el valor estimado, o pronóstico que buscamos realizar, mediante un cálculo realizado con una expresión sencilla. La primera se aplica a los valores observados en la serie de tiempo y la Suavización Exponencial Triple Este método se utiliza cuando además de presentarse una tendencia lineal en la serie de tiempo, hay también un patrón de comportamiento de tipo estacional o periódico en los datos o valores de la serie de tiempo. Esta técnica es una extensión del método de Holt ya que incorpora una ecuación para calcular una estimación de la estacionalidad. El método Holt-Winters se utiliza para hacer un pronóstico de comportamiento deuna serie temporal a partir de los datos obtenidos.Este método es una extensión del método Holt debido a que este considera solo 2exponentes en cambio el método Winters considera 3 factores de unadeterminada serie de tiempos los cuales son: Nivel – Tendencia – Estacionalidad Atenuación de la serie de tiempo. 𝑆𝑡 𝑋𝑡 𝑆𝑡 = + (1 − 𝛼)(𝑆𝑡−1 + 𝑇𝑡−1 ) 𝐸𝑡−𝐿 tasa prevista de demanda intermitente, y entendida como la razón “demanda/período” (Algoritmo del método de Croston) Estimación de la tendencia. 𝑇𝑡 = 𝛽(𝑆𝑡 − 𝑆𝑡−1 ) + (1 − 𝛽)𝑇𝑡−1 Estimación de la estacionalidad 𝑋𝑡 𝐸𝑡 = 𝛾 + (1 − 𝛾)𝐸𝑡−𝐿 𝑆𝑡 Pronóstico para p periodos en el futuro 𝑃𝑡+𝑝 = (𝑆𝑡 − 𝑝𝑇𝑡 )𝐸𝑡−𝐿+𝑝 Donde: ▪ 𝑆𝑡 : Es el nuevo valor atenuado suavizado. ▪ 𝛼: Es la constante de atenuación que toma valores en el intervalo 0,1 ▪ 𝑋𝑡 : Es la nueva observación o valor real de la serie en el momento t. ▪ 𝛽: La constante de atenuación de la estimación de la tendencia y toma valores en el intervalo Intervalo de 0,1. Es la estimación de la tendencia. ▪ 𝛾: Es la constante de atenuación de la estimación de la estacionalidad y toma valores en el intervalo. Es la estimación de la estacionalidad. ▪ p: el numero de periodos a pronosticar ▪ L: Longitud de la estacionalidad ▪ 𝑃𝑡+𝑝 : Es el pronóstico para p periodos en el futuro. • Método de Croston: Especial para productos con ventas intermitentes. Primero pronostica cuando habrá demanda y luego cuanto será demandado. Ambos pronósticos se hace utilizando el modelo de exponencial simple con el mismo Alpha. Crear pronóstico esporádico: Esta opción permite generar un pronóstico que respete los tiempos entre ventas pronosticados. El método de Croston (CRO) utiliza como base la atenuación exponencial simple separando la serie de tiempo en dos partes: la primera, una serie con valores positivos de demanda, y la segunda, con los tiempos entre demandas consecutivas no nulas. En cada una de esas series se estima la previsión por medio de suavización exponencial y luego, ambos valores son actualizados cuando existe un valor no nulo de demanda. En ambos casos se utiliza el mismo valor del parámetro de atenuación alfa (α). Una de las características particulares del método CRO es el resultado expresado en términos de una Donde: dt: demanda en el periodo t; 𝑑̂𝑡 : previsión de la demanda no nula para el período siguiente t; ft : tiempo entre dos demandas no nulas; 𝑓̂𝑡 : previsión del intervalo de demanda; k : intervalo desde la última demanda no nula; α : parámetro de atenuación, 0≤α≤1; m : demanda promedio en el período. Promedio • Promedio Simple El método de pronóstico simple, consiste en atenuar los datos al obtener la media aritmética de cierto número de datos históricos para obtener con este el pronóstico para el siguiente período. Este método es óptimo para patrones de demanda aleatorios o nivelados sin elementos estacionales o de tendencia. • Promedio Ponderado. • Promedio Móvil Simple El pronóstico de promedio móvil simple es óptimo para patrones de demanda aleatoria o nivelada donde se pretende eliminar el impacto de los elementos irregulares históricos • Promedio Móvil Ponderado Es una variación del promedio móvil. Mientras en el promedio móvil simple se le asigna igual importancia a cada uno de los datos que componen dicho promedio, en el promedio móvil ponderado se asigna una importancia específica (ponderación) a los datos para obtener el promedio, siempre que la sumatoria de las ponderaciones sea equivalente al 100%. Es una práctica regular aplicar el factor de ponderación mayor al dato más reciente. ARIMA Análisis de series temporales a través de un método más complejo y su aplicación requiere serie más largas. Box y Jenkins han desarrollado modelos estadísticos para series temporales que tienen en cuenta la dependencia existente entre los datos, esto es, cada observación en un momento dado es modelada en función de los valores anteriores. Los análisis se basan en un modelo explícito. Los modelos se conocen con el nombre genérico de ARIMA (AutoRegresive Integrated Moving Average), que deriva de sus tres componentes AR (Autoregresivo), I(Integrado) y MA (Medias Móviles). El modelo ARIMA permite describir un valor como una función lineal de datos anteriores y errores debidos al azar, además, puede incluir un componente cíclico o estacional. Es decir, debe contener todos los elementos necesarios para describir el fenómeno. Box y Jenkins recomiendan como mínimo 50 observaciones en la serie temporal. La metodología de Box y Jenkins se resume en cuatro fases: • La primera fase consiste en identificar el posible modelo ARIMA que sigue la serie, lo que requiere: ƒ Decidir qué transformaciones aplicar para convertir la serie observada en una serie estacionaria. ƒ Determinar un modelo ARMA para la serie estacionaria, es decir, los órdenes p y q de su estructura autorregresiva y de media móvil. • La segunda fase: Seleccionado provisionalmente un modelo para la serie estacionaria, se pasa a la segunda etapa de estimación, donde los parámetros AR y MA del modelo se estiman por máxima verosimilitud y se obtienen sus errores estándar y los residuos del modelo. • La tercera fase es el diagnostico, donde se comprueba que los residuos no tienen estructura de dependencia y siguen un proceso de ruido blanco. Si los residuos muestran estructura se modifica el modelo para incorporarla y se repiten las etapas anteriores hasta obtener un modelo adecuado. • La cuarta fase es la predicción, una vez que se ha obtenido un modelo adecuado se realizan predicciones con el mismo Auto regresión (p): ◦ Consta de usar la variable a predecir como su misma variable predictora. ◦ Se hace una regresión lineal que incluye p variables predictoras. ◦ Las p variables predictoras se construyen desfasando la historia de la variable a predecir de 1 a p periodos históricos Media Móvil (q): 𝑋𝑡 = 𝑐 + Ф1 ∗ 𝐿1 + Ф2 ∗ 𝐿2 + ⋯ + Ф𝑝 ∗ 𝐿𝑝 + 𝜀 ◦ Se construye el pronostico como resultado de una media móvil recursiva (similar al modelo exponencial de Brown) ◦ Busca reducir el ruido blanco, evitando el sobreajuste. ̂𝑡 = 𝑌̂𝑡−1 + 𝜃 ∗ 𝜀𝑡−1 𝑌̂ El resultado final es la siguiente ecuación lineal, donde tanto los valores desfasados (Lag´s) como el error están diferenciados d veces Formula matricial ARIMA: 𝑋𝑡 (𝐿)(1 − 𝐿)𝑑 𝐹𝑡 = 𝑌̂𝑡 (𝐿)𝜀𝑡 (1 − 𝐿)𝑑 𝐹𝑡 𝑒𝑠 𝑙𝑎 𝑝𝑎𝑟𝑡𝑒 𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑑𝑎 𝑋𝑡 (𝐿)𝑒𝑠 𝑙𝑎 𝑝𝑎𝑟𝑡𝑒 𝑎𝑢𝑡𝑜𝑟𝑟𝑒𝑔𝑟𝑒𝑠𝑖𝑣𝑎 𝑌̂𝑡 (𝐿) 𝑒𝑠 𝑙𝑎 𝑝𝑎𝑟𝑡𝑒 𝑑𝑒 𝑚𝑒𝑑𝑖𝑎 𝑚ó𝑣𝑖𝑙 𝜀𝑡 𝑒𝑠 𝑟𝑢𝑖𝑑𝑜 𝑏𝑙𝑎𝑛𝑐𝑜 Regresión Lineal Consiste en usar variables independientes correlacionadas con la variable dependiente para generar su pronóstico. Se requiere los valores históricos y futuros de las variables predictoras 𝑌 = 𝛽0 + 𝛽1 ∗ 𝑋1 + 𝛽2 ∗ 𝑋2 + ⋯ + 𝛽𝑛 ∗ 𝑋𝑛 Siendo 𝛽𝑛 el factor de cambio de Y al cambiar 𝑋𝑛 y manteniendo las demás variables constantes. La solución se encuentra utilizando el método de mínimos cuadrados. Árboles de decisión Se construyen en base a las variables independientes Se parte de un nodo que tiene todo el set de datos. Cada partición se hace en base a la variable dependiente que reduce más el error. El algoritmo termina cuando se llega al limite de profundidad o no hay suficientes datos en el nodo para seguir dividiéndolo. Un Árbol de Decisión (o Árboles de Decisiones) es un método analítico que a través de una representación esquemática de las alternativas disponible facilita la toma de mejores decisiones, especialmente cuando existen riesgos, costos, beneficios y múltiples opciones. El nombre se deriva de la apariencia del modelo parecido a un árbol y su uso es amplio en el ámbito de la toma de decisiones bajo incertidumbre (Teoría de Decisiones) junto a otras herramientas como el Análisis del Punto de Equilibrio. Los árboles de decisión son especialmente útiles cuando: Las alternativas o cursos de acción están bien definidas (por ejemplo: aceptar o rechazar una propuesta, aumentar o no la capacidad de producción, construir o no una nueva bodega, etc.) Las incertidumbres pueden ser cuantificadas (por ejemplo: probabilidad de éxito de una campaña publicitaria, probable efecto en ventas, probabilidad de pasar de etapas, etc.) Los objetivos están claros (por ejemplo: aumentar las ventas, maximizar utilidades, minimizar costos, etc.)