INSTITUCIÓN EDUCATIVA ESCUELA NORMAL SUPERIOR DE
Anuncio

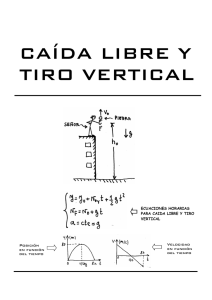
INSTITUCIÓN EDUCATIVA ESCUELA NORMAL SUPERIOR DE MEDELLÍN CAIDA LIBRE Y LANZMIENTO VERTICAL Grado: 10o Asignatura: FÍSICA Profesor: Nelson Correa Álvarez Objetivo: establecer las ecuaciones cinemáticas que se aplican a la caída de los cuerpos y al lanzamiento vertical cerca a la superficie terrestre. 𝑣𝑓 = 𝑣𝑖 − 𝑔 ∙ 𝑡 Caída libre 𝑦 = 𝑣𝑖 ∙ 𝑡 − Un caso particular de movimiento rectilíneo uniformemente acelerado, es el de un cuerpo que se mueve verticalmente, bajo la acción de la fuerza de gravedad. Cuando un objeto cae, su velocidad inicial, en el momento que se deja caer es cero, pero un tiempo después su velocidad cambia, es decir ha habido una aceleración, la aceleración debida a la gravedad (g) que tiene un valor aproximado de 9.8 m/s2, pues la aceleración debida a la gravedad varía ligeramente en distintos lugares de la tierra. Se dice que los objetos en movimiento solo bajo la influencia de la gravedad, están en caída libre. La aceleración debida a la gravedad g es constante para todos los objetos en caída libre, sin importar su masa ni su peso. 𝑦= (1) 𝑔∙𝑡 2 (2) 2 𝑣𝑓2 − 𝑣𝑖2 (3) 2𝑔 El origen y = 0 del sistema de referencia se toma usualmente como la posición inicial del objeto. El signo menos de g en las ecuaciones nos permite evitar los dobles signos en los ejercicios. Ejemplo: Un objeto que se suelta desde la parte más alta de un acantilado, tarda 1.8 s para llegar al agua del algo que hay debajo. ¿Cuál es la altura del acantilado sobre el agua? Solución Ecuaciones cinemáticas Datos: Por lo anterior podemos concluir que todas las ecuaciones del Movimiento Rectilíneo Uniformemente Acelerado, son válidas en el estudio del movimiento de los cuerpos en caída libre. Vi = 0 t = 1.8 s g = 9.8 m/s2 Y =? 𝑦 = 𝑣𝑖 ∙ 𝑡 − Se acostumbra utilizar Y para representar la dirección vertical y tomar el sentido hacia arriba como positivo, por tanto como la aceleración g debida a la gravedad siempre es hacia abajo, está en sentido negativo. 𝑔∙𝑡 2 2 𝑚 𝑦 =0∙𝑡 − 31.752𝑚 =− 2 9.8 2∙(1.8𝑠)2 𝑠 2 𝑚 = 9.8 2∙3.24𝑠2 − 𝑠 2 =-15.876 m El signo menos indica el sentido de la medición, hacia abajo. 2 Esta aceleración a = -g = -9.8 m/s , se puede sustituir en las ecuaciones de movimiento, así: 1 pelota? Y ¿Cuál es su altura máxima desde el punto de partida? Lanzamiento vertical De las ecuaciones anteriores podemos obtener otras igualmente útiles en la solución de problemas de caída libre y lanzamiento vertical. Veamos. 𝑡𝑣 = 3.2 𝑠 𝑡𝑣 = 2𝑣 3.2 𝑠∙9.8𝑚/𝑠2 2 0 − 𝑣𝑖2 −2𝑔 Ejercicios 𝑣𝑖2 2𝑔 1. Se deja caer una piedra desde una altura de 20 m ¿Cuánto tarda en caer al piso? ¿Qué velocidad tiene en el momento de llegar al piso? (4) 2. Con qué rapidez se debe lanzar un objeto hacia arriba para que alcance una altura de 12 m? 𝑣𝑓 = 𝑣𝑖 − 𝑔 ∙ 𝑡 3. Se tira una piedra hacia abajo con una velocidad de 12.4 m/s desde una altura de 65 m ¿Qué tan lejos llega en 2 s? ¿Cuál es su velocidad cuando llega al piso? 0 = 𝑣𝑖 − 𝑔 ∙ 𝑡𝑠 𝑣𝑖 𝑔 (5) Se puede demostrar que el tiempo empleado en alcanzar la altura máxima , es igual al tiempo empleado en caer desde allí, luego el tiempo que demora el objeto en el aire que denominaremos tiempo de vuelo es igual al doble del tiempo de subida. 𝑡𝑣 = = 𝑣𝑖 15.68 m/s = vi Si queremos calcular el tiempo empleado en alcanzar dicha altura, como la velocidad en este punto es cero, basta escribir vf = 0 en la ecuación (1) y despejar t. 𝑡𝑠 = 2 𝑣𝑖 𝑔 𝑖 3.2 𝑠 = 9.8𝑚/𝑠 2 Luego 𝑦𝑚𝑎𝑥 = vi=? Empleamos la ecuación: Cuando lanzamos un cuerpo verticalmente hacia arriba, este va disminuyendo su velocidad hasta que en un punto esta es cero y luego empieza a descender nuevamente. Este punto se conoce como su altura máxima. 𝑦𝑚𝑎𝑥 = g = 9.8 m/s2 2 𝑣𝑖 𝑔 4. Si dejamos caer una piedra desde una altura de 50 m ¿Cuál será su posición y distancia recorrida a los 3 s de haberla soltado?¿Qué velocidad posee en ese momento?¿Cuánto tarda en llegar al suelo? 5. Se lanza un objeto verticalmente hacia arriba con una velocidad de 30 m/s ¿cuál es su posición y velocidad al cavo de 1 s? ¿Cuál será su altura máxima alcanzada y en qué tiempo? ¿Cuál será su velocidad al llegar al suelo y el tiempo empleado? (6) Ejemplo: Una pelota de beisbol lanzada verticalmente hacia arriba se cacha a la misma altura 3.2 s después ¿Cuál es la velocidad inicial de la 2