Portada del equipo 12
Sistemas Distribuidos Paralelos.
Grupo:
Hora:
Días clase:
Nombre
Ranfery Josua
Peregrina
Morales
José Antonio
Rodríguez
Basaldua
José Homero
Rodríguez
Basaldua
Angie Abigail
Monteverde
Tapia
004
N4
Lun, Mie, Vie
Matrícula Carrera Oportunidad
1924910
ITS
Primera
1838254
ITS
Primera
1838253
ITS
Primera
1882021
ITS
Primera
Resumen: Grafos senderos y ciclos
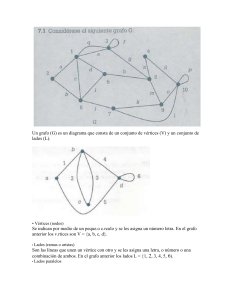
Definición de Grafo
Un grafo es una estructura matemática que se utiliza para representar relaciones entre objetos. En
un grafo, los objetos se representan como nodos o vértices, y las relaciones entre ellos se
representan como líneas o arcos que conectan estos vértices.
Los grafos pueden ser utilizados en una amplia variedad de aplicaciones, como la representación
de redes sociales, redes de transporte, mapas de internet y mucho más.
Hay dos tipos básicos de grafos: grafos dirigidos y grafos no dirigidos. En un grafo dirigido o grafo
"dígrafos", cada arco o relación tiene una dirección asociada, es decir, un vértice inicial y un vértice
final. En otras palabras, si hay un arco desde el vértice A hasta el vértice B, no hay necesariamente
un arco desde el vértice B hasta el vértice A.
Por otro lado, en un grafo no dirigido o grafo "no dígrafos", las relaciones entre vértices son
bidireccionales, es decir, si hay una relación entre dos vértices, entonces existe una relación en
ambas direcciones.
Es importante tener en cuenta que esta diferencia tiene implicaciones importantes en la forma en
que se analizan y se utilizan los grafos. Por ejemplo, en un grafo dirigido, se pueden utilizar
conceptos como flujos y caminos críticos para modelar problemas de optimización y gestión,
mientras que, en un grafo no dirigido, se utilizan conceptos como componentes conexas y árboles
para representar relaciones de contención.
Definición de Path
Un “Path” traducido al español como sendero es una secuencia de vértices en los que cada vértice
consecutivo está conectado por un arco.
Un sendero es diferente de un camino en que un camino puede tener vértices repetidos, mientras
que un sendero no puede tener vértices repetidos.
Hay diferentes tipos de senderos, como senderos simples, senderos cíclicos y senderos conexos,
dependiendo de las propiedades de la secuencia de vértices y arcos. Por ejemplo, un sendero
cíclico es un sendero que comienza y termina en el mismo vértice.
Definición de Ciclo
Un ciclo en un grafo es un camino que comienza y termina en el mismo vértice y que pasa por al
menos un vértice adicional. Es decir, un ciclo es un camino que no es una línea recta, sino que
regresa al mismo vértice al menos una vez.
Un ciclo en un grafo puede ser tanto simple como no simple. Un ciclo simple es un ciclo en el que
cada vértice aparece exactamente una vez, excepto por el vértice inicial y final, que son iguales.
Un ciclo no simple, por otro lado, puede tener vértices repetidos.
Los ciclos en los grafos son importantes porque pueden ser utilizados para representar relaciones
cíclicas en diferentes aplicaciones. Por ejemplo, en un grafo de tareas, un ciclo puede indicar una
dependencia circular entre tareas, lo que podría ser un problema. También pueden ser utilizados
en la detección de ciclos y en la identificación de componentes conexas en un grafo.
Vertex Relationship
"Vertex relationship" es un término que se refiere a la relación entre vértices en un grafo. En
teoría de grafos, los vértices representan objetos o entidades, y las relaciones entre ellos
representan las conexiones o asociaciones entre estas entidades.
Todos lo predecesores también son ancestros y todos los sucesores también son descendientes.
Representación en una computadora
Hay varias formas de representar un grafo en una computadora, el video aborda dos de ellas:
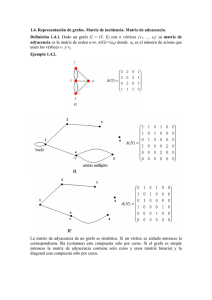
Matriz de Adyacencia:
La matriz de adyacencia es una forma común de representar un grafo en una computadora. En
esta representación, se utiliza una matriz cuadrada para representar los vértices del grafo y sus
relaciones. La entrada en la fila i y la columna j de la matriz se utiliza para representar un arco
desde el vértice i hasta el vértice j.
Si hay un arco desde el vértice i hasta el vértice j, la entrada correspondiente en la matriz se
establece en 1, y si no hay un arco, la entrada se establece en 0. La matriz de adyacencia es
simétrica si el grafo es no dirigido, es decir, si hay un arco desde el vértice i hasta el vértice j,
entonces también hay un arco desde el vértice j hasta el vértice i.
La matriz de adyacencia es una forma eficiente de representar grafos densos, es decir, grafos con
muchos arcos. Sin embargo, para grafos dispersos, es decir, grafos con pocos arcos, la matriz de
adyacencia es menos eficiente en términos de espacio de almacenamiento, ya que la mayoría de
las entradas en la matriz estarán en 0.
Además, la matriz de adyacencia es muy eficiente para realizar operaciones básicas en grafos,
como calcular el grado de un vértice, encontrar los vértices adyacentes a un vértice dado, y
determinar si existe un camino entre dos vértices.
En resumen, la matriz de adyacencia es una forma eficiente y directa de representar grafos, y es
una herramienta importante en la teoría de grafos y en la solución de problemas relacionados con
grafos en la computadora.
Lista de adyacencias
La lista de adyacencia es otra forma común de representar un grafo en una computadora. En esta
representación, cada vértice del grafo se representa como un nodo en una estructura de datos, y
cada arco se representa como un enlace entre los nodos correspondientes.
Por ejemplo, si hay un arco desde el vértice A hasta el vértice B, entonces la lista de adyacencia del
vértice A incluirá a B como uno de sus vértices adyacentes. Esta representación es eficiente para
grafos con muchos vértices y pocos arcos, ya que el tamaño de la representación depende del
número de arcos en el grafo, no del número de vértices.
En la lista de adyacencia, cada vértice se almacena en una estructura de datos, como una lista o
una tabla hash, y se puede acceder a su lista de adyacencia mediante un índice o una clave
asociada al vértice. Las operaciones en un grafo representado como una lista de adyacencia
incluyen la inserción y eliminación de vértices y arcos, la búsqueda de vértices y arcos, y la
realización de recorridos en el grafo.
La lista de adyacencia es una forma flexible y fácil de manipular de representar grafos, y se utiliza
comúnmente en aplicaciones de grafos, como la búsqueda en grafos, el camino más corto y la
detección de ciclos.
En resumen, la lista de adyacencia es una forma eficiente y flexible de representar grafos en una
computadora, y es una herramienta importante en la teoría de grafos y en la solución de
problemas relacionados con grafos en la computadora.
Máximo número de aristas
El número máximo de aristas en un grafo depende del número de vértices en el grafo. Hay dos
tipos de grafos, grafos no dirigidos y grafos dirigidos, y el número máximo de aristas para cada uno
de ellos es diferente.
Para un grafo no dirigido con n vértices, el número máximo de aristas es n * (n - 1) / 2. Esto se
debe a que cada vértice puede tener un máximo de n - 1 vértices adyacentes, y el número total de
arcos sería la mitad del número de pares de vértices adyacentes.
Para un grafo dirigido con n vértices, el número máximo de aristas es n * (n - 1). Esto se debe a
que cada vértice puede tener un máximo de n - 1 arcos salientes, y el número total de arcos sería
la suma de los arcos salientes desde cada vértice.
En resumen, el número máximo de aristas en un grafo depende del número de vértices y si el
grafo es no dirigido o dirigido. Para un grafo no dirigido con n vértices, el número máximo de
aristas es n * (n - 1) / 2, y para un grafo dirigido con n vértices, el número máximo de aristas es n *
(n - 1).
Algoritmos de búsqueda elementales.
Aquí vemos 2 algoritmos de búsqueda que aplican teoría de grafos y son considerados los 2
algoritmos más importantes de esta característica.
BFS (Breadth-First Search)
BFS es un algoritmo de búsqueda en grafos que se utiliza para explorar todos los vértices de un
grafo en un orden determinado. BFS se basa en la idea de explorar primero todos los vértices
adyacentes a un vértice dado antes de explorar vértices más alejados.
El proceso de BFS se realiza en dos fases:
1. Marcar el vértice inicial como visitado y agregarlo a una cola.
2. Mientras la cola no esté vacía, extraer un vértice de la cola y marcarlo como visitado.
Luego, para cada vértice adyacente no visitado, marcarlo como visitado y agregarlos a la
cola.
BFS es útil para muchas aplicaciones, incluyendo:
•
•
•
•
Encontrar el camino más corto entre dos vértices en un grafo no ponderado.
Determinar si existe un camino entre dos vértices en un grafo.
Encontrar componentes conexas en un grafo no dirigido.
Encuentre la distancia mínima entre dos vértices en un grafo ponderado.
En resumen, BFS es un algoritmo de búsqueda en grafos que explora los vértices en un orden
determinado y es útil para muchas aplicaciones, incluyendo encontrar caminos más cortos,
determinar la conectividad y encontrar componentes conexas.
DFS (Depth-First Search)
DFS es un algoritmo de búsqueda en grafos que se utiliza para explorar los vértices de un grafo en
un orden profundo. A diferencia de BFS, que explora primero los vértices adyacentes a un vértice
antes de explorar vértices más alejados, DFS explora primero un camino profundo hacia abajo
antes de regresar y explorar otro camino.
El proceso de DFS se realiza en dos fases:
1. Marcar el vértice inicial como visitado y empujarlo a una pila.
2. Mientras la pila no esté vacía, extraer un vértice de la pila. Para cada vértice adyacente no
visitado, marcarlo como visitado y empujarlo a la pila.
DFS es útil para muchas aplicaciones, incluyendo:
•
•
•
•
•
Encontrar componentes conexas en un grafo no dirigido.
Encontrar ciclos en un grafo
Encontrar camino entre dos vértices en un grafo.
Realizar una clasificación topológica en un grafo dirigido acíclico.
Encuentre la distancia mínima entre dos vértices en un grafo no ponderado.
En resumen, DFS es un algoritmo de búsqueda en grafos que explora los vértices en un orden
profundo y es útil para muchas aplicaciones, incluyendo encontrar componentes conexas, ciclos,
caminos y realizar una clasificación topológica.
Orden topológico
Un orden topológico de un grafo acíclico dirigido G = {P;E} es una ordenación lineal de todos sus
vértices tal que E contiene una arista entonces u aparecerá antes de v en el orden.
Orden topológico y un grafo dirigido
Un grafo dirigido G = {P, E} es acíclico siempre y cuando exista un orden topológico en sus vértices,
a continuación, se muestra una representación de grafica de un grado acíclico dirigido
Y aquí se muestra el mismo grafico ordenado de forma topológico
Gráfico como modelo de programa
Cuando hablamos de una abstracción teórica de grafos, un programa constara de dos tipos de
actividad:
•
•
Computación: asociada con vértices de la grafica
Comunicación: asociada con las aristas de la grafica
Vértices
En este caso el vértice sería el nodo y el computo asociado a la tarea, hay que tomar en cuenta
que una tarea puede variar desde una instrucción u operación atómica hasta hilos o declaraciones
compuestas como bucles, bloques básicos y secuencias de estos.
Nodos
Un nodo no puede comenzar a ejecutarse hasta que hayan llegado todas sus entradas y ninguna
salida esté disponible hasta que termine, en el momento en que termine todas las salidas deben
estar disponibles nuevamente para la comunicación simultánea.
Costos de computación y de comunicación
Normalmente estos costos se miden con tiempo en base al tiempo que tarda un cómputo o una
comunicación en el sistema de destino y esto se incorpora al modelo d e grafico mediante la
asignación de pesos a los elementos del gráfico.
Criterios de comparación
•
•
•
Tipos de cómputo:
Esto engloba el cuestionamiento de que tipo de cálculos de pueden representar
eficientemente con el modelo gráfico, dichos modelos gráficos pueden ser distinguidos en
cuanto a la granularidad modelada y la capacidad de reflejar cálculos iterativos.
Arquitectura paralela:
Este criterio responde el cuestionamiento de para que arquitectura de sistema paralelo
suele emplear el modelo gráfico, los modelos paralelos genéricos pueden ser clasificados
en base a su tipo de instrucción y flujo de datos, su arquitectura de memoria y su modelo
de programación.
Técnicas y algoritmos:
Con este criterio respondemos el cuestionamiento de cuales serían aquellos algoritmos y
técnicas que pueden ser aplicadas al modelo grafico siendo estos generalmente utilizados
para análisis de dependencia, transformaciones de programas, mapeo y programación.
Grafo de flujo
El grafo de flujo (FG) consigue una representación concisa de la estructura de un cálculo iterativo
introduciendo información de temporización en el grafo para poder distinguir entre comunicación
“intra” e “inter” iteración.
El grafo de flujo tiene dos características esenciales, siendo la primera de ellas que sus nodos
representan tareas que pueden ejecutarse varias veces, y no instancias de tareas donde cada nodo
representado se ejecuta exactamente una vez, también, el grafo de flujo no es generalmente
acíclico. Pero pueden surgir ciclos en relación con la dependencia entre iteraciones con el
resultado siendo factible
Modelo de ejecución basado en datos
Un nodo puede empezar su ejecución si cada arista de entrada contiene un numero positivo de
fichas y cada arista de salida tiene al menos un espacio en la cola. Hay que tomar en cuenta que
antes de iniciar la ejecución el nodo eliminara una ficha de cada arista de entrada y colocara una
ficha en cada arista de salida después de finalizar la ejecución. Este modelo de fichas es
considerado un modelo de ejecución basado en datos.
Gráficos de dependencia (DG)
En este tema se analizan las relaciones de dependencia dirigidas entre tareas. Uno podrías
representar las tareas de los programas como nodos y las relaciones de dependencia como aristas,
correspondientes al modelo de grafos definida. Representando cada tarea por un nodo y toda
relación de dependencia por una arista desde la causa hasta la tarea dependiente se obtiene un
gráfico que refleja la estructura de dependencia.
Un gráfico de dependencia es un tipo de grafo que representa las relaciones de dependencia entre
elementos o componentes. En un gráfico de dependencia, los nodos representan los componentes
y las aristas representan las dependencias entre ellos.
Los gráficos de dependencia se utilizan en muchas áreas, como la programación, la gestión de
proyectos y la ingeniería de software. En la programación, por ejemplo, los gráficos de
dependencia se utilizan para representar las relaciones entre módulos de software, módulos de
bibliotecas o clases en un sistema.
En un gráfico de dependencia, un bucle anidado puede ser representado mediante una
dependencia circular entre los componentes involucrados en el bucle. Esto significa que un
componente A depende de un componente B, mientras que el componente B depende del
componente A.
Los bucles anidados pueden ser un problema en la resolución de problemas o en la planificación
de tareas, ya que pueden causar una dependencia infinita y hacer que el sistema se bloquee. Por
lo tanto, es importante identificar y resolver los bucles anidados en un gráfico de dependencia.
Hay varios enfoques para resolver los bucles anidados en un gráfico de dependencia. Un enfoque
común es modificar la dependencia para que no haya una dependencia circular. Por ejemplo, se
puede agregar un componente intermediario para romper la dependencia circular o se pueden
reorganizar los componentes para evitar la dependencia circular.
Otro enfoque es utilizar técnicas de programación como el control de flujo para evitar el bucle
anidado. Por ejemplo, se pueden agregar condicionales para salir del bucle cuando se cumpla una
determinada condición.
Los gráficos de dependencia pueden ser útiles para visualizar la estructura de un sistema y para
identificar dependencias y relaciones complejas. También pueden ayudar a detectar problemas de
diseño, como dependencias circulares, y a planificar el orden de las tareas durante la resolución de
problemas.
Conclusiones;
José Antonio Rodríguez Basaldua
José Homero Rodríguez Basaldua
Ranfery Josua Peregrina Morales
Angie Abigail Monteverde Tapia