C1_RepresentacionComputador

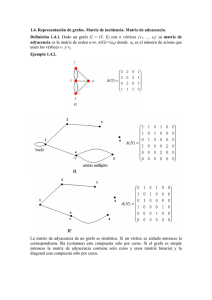
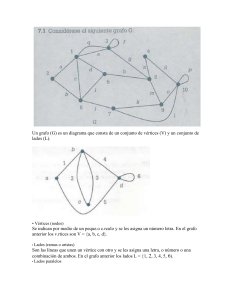
1.5. Representación de grafos en el computador.
Los grafos pueden representarse estructuras de datos distintas. Los algoritmos que se
aplican sobre ellos adoptan tiempos distintos dependiendo de la forma de representación
elegida. En particular, los tiempos de ejecución variarán en función del número de
vértices y el de aristas, por lo que la utilización de una representación u otra dependerá
en gran medida de si el grafo es denso (cuando tiene muchas aristas) o disperso (muy
pocas aristas).
Definición 1.5.1. Sea G = (V, E) un grafo simple con n=|V|, m=|E| . Definiremos la
densidad del grafo como
d
2m
n(n  1)
Notar que 0  d  1, donde d=0 si todos los vértices son aislados y d=1 si el grafo es
completo. Si d es cercano a cero se dice que el grafo es disperso y si d es cercano a 1 se
dice que el grafo es denso.
Las representaciones más utilizadas de representación de los grafos son:
a. Representación por matriz de adyacencia
b. Representación por listas de adyacencias.
La matriz de adyacencia es la forma más común de representación y la más directa.
Consiste en una tabla de tamaño nxn, en que la que aij tendrá como valor 1 si existe una
arista del vértice i al vértice j. En caso contrario, el valor será 0. Si el grafo es no
dirigido hay que asegurarse de que se marca con un 1 tanto la entrada aij como la
entrada aji, puesto que se puede recorrer en ambos sentidos.
Como se puede apreciar, la matriz de adyacencia siempre ocupa un espacio de n2, es
decir, depende solamente del número de nodos y no del de aristas, por lo que será útil
para representar grafos densos.
Definición 1.5.2. Una lista de adyacencia consiste de una lista de los vértices del grafo
y para cada vértice de una lista de sus vértices vecinos.
Ejemplo 1.5.3.:
Lo que se hace es definir una lista enlazada para cada nodo, que contendrá los nodos a
los cuales es posible acceder. Es decir, un vértice i tendrá una lista enlazada asociada en
la que aparecerá un elemento con una referencia al vértice j si i y j tienen una arista que
los une. Obviamente, si el grafo es no dirigido, en la lista enlazada de j aparecerá la
correspondiente referencia al vértice i. En este caso el espacio ocupado es nm, muy
distinto del necesario en la matriz de adyacencia, que era de n2. La representación por
listas de adyacencia, por tanto, será más adecuada para grafos dispersos.
Un aspecto importante es que la implementación con listas de adyacencias determina
fuertemente el tratamiento del grafo posterior. Una consecuencia de esto es que si un
problema tiene varias soluciones la primera que se encuentre dependerá de la entrada
dada. Podría presentarse el caso de tener varias soluciones y tener que mostrarlas
siguiendo un determinado orden. Ante una situación así podría ser conveniente
modificar la forma de meter los nodos en la lista de manera que el algoritmo mismo
diera las soluciones ya ordenadas.
Tarea: Escribir dos programas uno que utilice la matriz de adyacencia y otro utilice las
listas de adyacencias para almacenar el grafo simple G(V,E) y que resuelvan los
siguientes problemas:
1. Dado i, determinar el grado de vi
2. Determinar si G es bipartido.
Generar aleatoriamente grafos de diferente densidad y comparar los resultados.