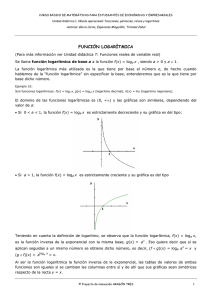
Función logarítmica Función logarítmica El Arco Gateway, también conocido con el nombre de Puerta hacia El Oeste, se encuentra situado en la orilla del Río Mississippi, en la ciudad de San Luis, Estado de Misuri, en Estados Unidos, y con sus casi 200 metros de altura es el monumento más alto del mundo construido por el hombre. ¿Qué función se involucra en la ecuación matemática usada para construir el arco? Función logarítmica La función logaritmo natural Ejercicio 1: Dibuja con la función logaritmo natural. Mirando la gráfica indica las características que tiene la función (dominio, recorrido, continuidad, concavidad … ) Función logarítmica La función logaritmo natural Ejercicio 1: Dibuja con la gráfica de la función logaritmo natural. Mirando la gráfica indica las características que tiene la función (dominio, recorrido, continuidad, concavidad … ) Función logarítmica La función logaritmo natural Ejercicio 2: Traza la gráfica con las siguientes funciones e indica su dominio. a) c) b) d) Función logarítmica La función logaritmo natural Ejercicio 2: Traza la gráfica con las siguientes funciones e indica su dominio. a) c) b) d) Función logarítmica Función logarítmica Recuerda: Propiedades de los logaritmos Función logarítmica Recuerda: Propiedades de los logaritmos Ejemplo 1: Desarrollo de expresiones logarítmicas Función logarítmica Recuerda: Propiedades de los logaritmos Ejemplo 1: Desarrollo de expresiones logarítmicas Otro ejemplo Derivación Función logarítmica Derivada de la función logaritmo natural Ejemplo 2: Derivación de una función logarítmica Derivación Derivada de la función logaritmo natural Ejemplo 3: Derivación de una función logarítmica Función logarítmica Derivación Función logarítmica Derivada de la función logaritmo natural Ejemplo 4: Propiedades de los logaritmos ayudan en la derivación a) Derivar 𝑓 𝑥 = ln( 𝑥 + 1) Derivación Función logarítmica Derivada de la función logaritmo natural Ejemplo 4: Propiedades de los logaritmos ayudan en la derivación b) Derivar 𝑥(𝑥 2 +1)2 𝑓 𝑥 = ln( 2𝑥 3 −1 ) Función logarítmica Integración Integración de la función logaritmo natural Ejemplo 5: Uso de la regla de logaritmo para integración Ejemplos Como 𝑥 2 no puede ser negativa, el valor absoluto no es necesario. Integración Función logarítmica Integración de la función logaritmo natural Ejemplo 6: Uso de la regla de logaritmo con cambio de variable Ejemplo Integración Función logarítmica Integración de la función logaritmo natural Ejemplo 7: Integración de cocientes para la regla de logaritmo Otro ejemplo Integración Función logarítmica Ejemplo 8: Cambio de variable con la regla de logaritmo. Ejemplo Función logarítmica Integración Las integrales a las que se aplica la regla de logaritmo aparecen a menudo disfrazadas. Por ejemplo, si una función racional tiene un numerador de grado mayor o igual que el del denominador, la división puede revelar una forma a la que se pueda aplicar la regla de logaritmo. Esto se muestra en el siguiente ejemplo. Ejemplo 9: Usar división larga antes de integrar. Integración Ejemplo 9: Usar división larga antes de integrar. Función logarítmica Función logarítmica Integración Con la regla de logaritmo, se puede completar el conjunto de reglas básicas de integración trigonométricas. Ejemplo 10: Integración Función logarítmica Con la regla de logaritmo, se puede completar el conjunto de reglas básicas de integración trigonométricas. Integración Integración de la función logaritmo natural Ejemplo 10: Cálculo de un área con la regla de logaritmo. Función logarítmica Integración Integración de la función logaritmo natural Ejemplo 10: Cálculo de un área con la regla de logaritmo. Función logarítmica