arturo

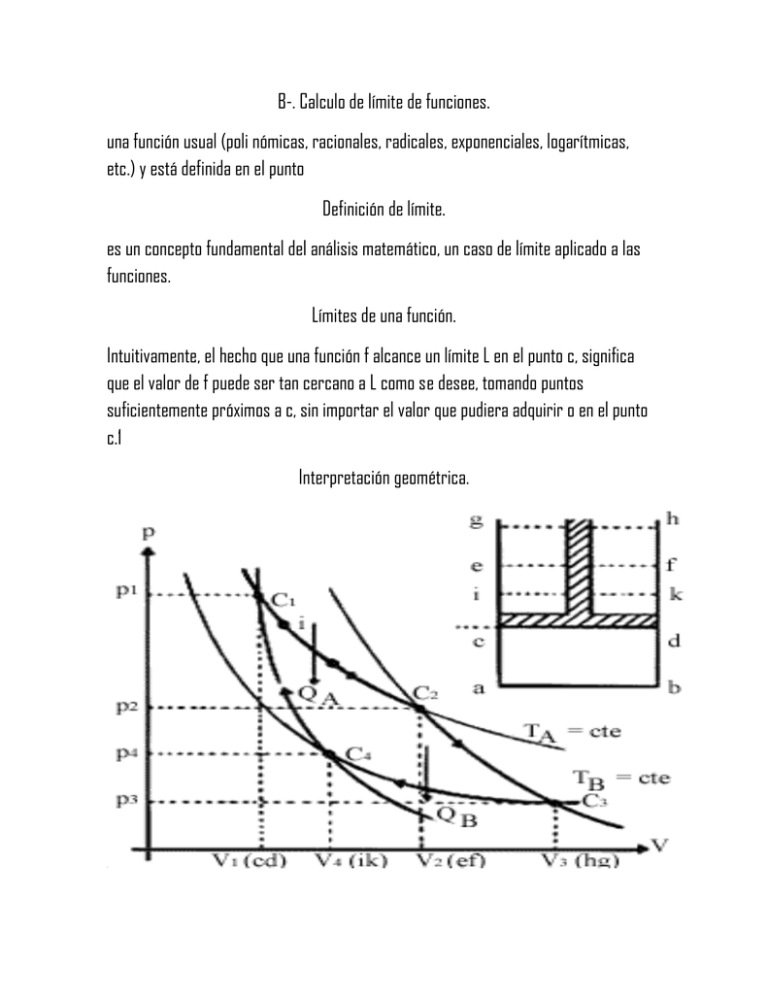
B-. Calculo de límite de funciones.
una función usual (poli nómicas, racionales, radicales, exponenciales, logarítmicas,
etc.) y está definida en el punto
Definición de límite.
es un concepto fundamental del análisis matemático, un caso de límite aplicado a las
funciones.
Límites de una función.
Intuitivamente, el hecho que una función f alcance un límite L en el punto c, significa
que el valor de f puede ser tan cercano a L como se desee, tomando puntos
suficientemente próximos a c, sin importar el valor que pudiera adquirir o en el punto
c.1
Interpretación geométrica.
Limites por la izquierda y por la derecha.
El concepto de límite por la izquierda es completamente similar al límite por la derecha, solo que la variable
x se acerca al valor a por la izquierda, es decir, con valores que son menores a a. Considere el lector la
función
cuya gráfica acompaña este texto. Observe que el dominio de
esta función es el intervalo abierto
ni para ningún valor superior a éste.
, es decir que la función no está definida ni para
Limite por derecha.
Que aparece representada a la izquierda de este texto. Observe que la función está definida sobre el
intervalo abierto
. En particular no está definida para
, lo cual está indicado
en la gráfica por un pequeño círculo azul con relleno blanco situado al extremo izquierdo de la curva, justo
sobre el valor
.
Suma de límites.
Límite de una suma de funciones
El límite de una suma de dos funciones convergentes, es igual a la suma de los límites de cada una de ellas:
Límite de una resta de funciones
El límite de una resta de dos funciones convergentes, es igual a la diferencia de los
límites de cada una de ellas:
Límite de un producto de funciones
El límite de un producto de dos funciones convergentes, es igual al producto de los límites de cada una de
ellas:
Límite de un cociente de funciones
El límite de un cociente de dos funciones convergentes es igual al cociente de los límites de cada una de
ellas, si el denominador no es nulo:
Diferencia.
El término diferencia1 puede hacer referencia a: Lo contrario a la igualdad, tanto en términos matemáticos
como sociales y otros. Lo contrario de la identidad, tanto en términos matemáticos como lógicos,
filosóficos, sociales y otros.
De una constante.
En general, una constante es un valor de tipo permanente, que no puede modificarse, al menos no dentro del
contexto o situación para el cual está: geometría aritmética.
En ciencias, especialmente en física, se denomina constante a aquella magnitud cuyo valor no varía en el
tiempo.
En matemáticas, una constante es un valor fijo, aunque a veces no determinado.
Una Función constante es una función matemática que para cada conjunto de variables en la misma,
devuelve el mismo valor.
En álgebra son los coeficientes de un monomio u otra fórmula. En ecuaciones diferenciales al resolver se
obtiene una solución general con constante ( o constantes), si es de primer orden conlleva una constante
arbitraria o constante de integración.1
Constante es un elemento utilizado en lenguajes de programación.
De una constante multiplicada por una función.
En matemáticas, una constante es un valor fijo, aunque a veces no determinado. Una Función constante es
una función matemática que para cada conjunto de variables en la misma, devuelve el mismo valor.
De un producto.
n producto es una opción elegible, viable y repetible que la oferta pone a disposición de la demanda, para
satisfacer una necesidad o atender un deseo a través de su uso o consumo.1 El producto es uno de los
componentes estructurales de la mezcla de mercadotecnia
Cociente.
Espacio cociente es un término matemático que hace referencia a cierta estructura matemática que se
deriva de otra en la que se ha definido una relación de equivalencia.
De manera más precisa, si X es una estructura matemática en el que se define una relación de equivalencia
~, entonces el espacio cociente X/~ es la estructura matemática inducida en el conjunto de clases de
equivalencia con las operaciones entre clases de equivalencia obtenidas de manera canónica a partir de las
correspondientes en X.
Potencia.
es la cantidad de trabajo efectuado por unidad de tiempo.
C.-continuidad y límites de una función.
Continuidad de una función.
Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:
1. Que el punto x = a tenga imagen.
2. Que exista el límite de la función en el punto x = a.
3. Que la imagen del punto coincida con el límite de la función en el punto.
Funciones continua y discontinua.
Continuidades
Una función es continua en un punto si existe límite en él y coincide con el valor que toma la función en ese punto.
Una idea intuitiva de función continua se tiene al considerar que su gráfica es continua, en el sentido que se puede dibujar sin
levantar el lápiz de la hoja de papel.
Continuidad de una función en un punto
Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:
1. Que el punto x= a tenga imagen.
2. Que exista el límite de la función en el punto x = a.
3. Que la imagen del punto coincida con el límite de la función en el punto.
Si una función no es continua en un punto x=a, diremos que es discontinua en dicho punto.
Una función es continua por la derecha en un punto si existe el límite por la derecha en él y coincide con el valor que toma la
función en ese punto, es decir
Una función es continua por la izquierda en un punto si existe el límite por la izquierda en él y coincide con el valor que toma la
función en ese punto.
as1dda
Discontinuidades
1.- Una función es discontinua en un punto cuando no existe límite en él o, existiendo, no coincide con el valor de la función en el
mismo.
2.- Una función tiene una discontinuidad evitable en un punto cuando existe límite en él y no coincide con el valor de la función en
el mismo.El valor que deberíamos dar a la función en dicho punto para que fuera continua en él se llama verdadero valor de la
función en el mismo.
3.- Una función tiene una discontinuidad inevitable.
Continuidad de una función en un punto.
Una función (f) es continua en un punto (x) en el dominio de la función.
Continuidad de una función en un intervalo.
Una función es continua en un intervalo abierto (a, b) si es lo que en cada uno de sus puntos