fhgjk
Anuncio

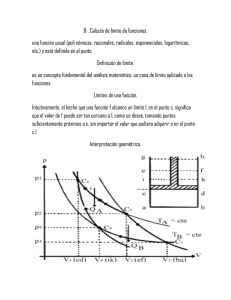
B. Calculo de límites de funciones Límites de una Funcion Se dice que una función y=f(x) tiene límite "l" cuando la x tiende a "a" y lo representamos por: Definición de Limites Cuando para toda sucesión de números reales que se aproxime a "a" tanto como queramos, los valores correspondientes de f(x) se aproximan a "l" tanto como queramos. ("tanto como queramos" es una expresión que nos indica que la aproximación será tanto mayor cuantos más elementos tomemos de la sucesión). Interpretación de geométrica Limites por la Izquierda y por la Derecha Por la Izquierda: El concepto de límite por la izquierda es completamente similar al límite por la derecha, solo que la variable x se acerca al valor a por la izquierda, es decir, con valores que son menores a a. Por la Derecha: la función que aparece representada a la izquierda de este texto. Observe que la función está definida sobre el intervalo abierto . En particular no está definida para , lo cual está indicado en la gráfica por un pequeño círculo azul con relleno blanco situado al extremo izquierdo de la curva, justo sobre el valor . Suma de Limite Límite de una suma de funciones El límite de una suma de dos funciones convergentes, es igual a la suma de los límites de cada una de ellas: Límite de una resta de funciones El límite de una resta de dos funciones convergentes, es igual a la diferencia de los límites de cada una de ellas: Límite de un producto de funciones El límite de un producto de dos funciones convergentes, es igual al producto de los límites de cada una de ellas: Límite de un cociente de funciones El límite de un cociente de dos funciones convergentes es igual al cociente de los límites de cada una de ellas, si el denominador no es nulo: Diferencia El término diferencia puede hacer referencia a: Lo contrario a la igualdad, tanto en términos matemáticos como sociales y otros. Lo contrario de la identidad, tanto en términos matemáticos como lógicos, filosóficos, sociales y otros. Constante Una constante es un valor de tipo permanente, que no puede modificarse, al menos no dentro del contexto o situación para el cual está: geometría aritmética Una Constante multiplicada por una Función Una Función constante es una función matemática que para cada conjunto de variables en la misma, devuelve el mismo valor Producto En matemáticas, producto es sinónimo de multiplicación. Se denominan también producto ciertas operaciones binarias realizadas en contextos especializados. Cociente El resultado de una división recibe el nombre de cociente Potencia La potenciación es la operación matemática mediante la cual multiplicamos un número por sí mismo las veces que nos indique elexponente. Partes del número con exponente Por ejemplo, la ecuación ecuación donde a es un número cualquiera, equivale a la es decir que cumplimos la condición de multiplicar por sí mismo nuestro número (a) tres veces, tal como lo indicó el exponente (3) C. Continuidad y limites de una Función Continuidad de una Función Una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Funciones Continuas y Discontinuas Continuas: Que la gráfica de una función que es continua en un intervalo, es una línea ininterrumpida(es decir, una que se puede trazar sin levantar la pluma o lápiz del papel) Discontinua: Una función es discontinua cuando, una función f definida en un intervalo abierto que contenga aɑ es discontinua en ɑ si: f no tiene limite cuando x —> ɑ —> ɑ, f tiene un límite diferente de f(ɑ) f no está definida en ɑ, no es continua allí. Sin embargo, si f no está definida en ɑ pero si está definida para todos los valores cercanos, entonces no solo no es continua en ɑ, es discontinua allí. Continuidad de una Función en un Punto Definición de continuidad en un punto Una función f es continua en un punto x0 en el dominio de la función Continuidad de una Función en un intervalo Una función es continua en un intervalo abierto (a, b) si lo es en cada uno de sus puntos.