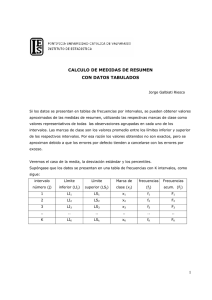
DATOS AGRUPADOS . Nro de clases=8
Anuncio

Datos Discretros 50 58 64 54 57 63 60 63 65 61 65 65 55 57 58 64 66 68 53 61 64 62 64 66 76 77 65 72 78 79 67 70 62 64 68 70 73 75 67 74 1.-CONSTRUIR LA TABLA DE DISTRIBUCIÓN 2.-CALCULAR LAS MEDIDAS DE TENDENCIA CENTRAL 3.- CALCULAR EL PERCENTIL 70, EL DECIL 30 Y EL QUARTIL 3 4.- INTERPRETAR EN EL SEGUNDO INTERVALO LA FRECUENCIA ORDINARIA RELATIVA (h) 5.- INTERPRETAR EN EL CUARTO INTERVALO LA FRECUENCIA ACUMULADA RELATIVA (H) 6 INDIQUE ELTIPO DE VARIABLE Y SU CORRESPONDIENTE ESCALA DE MEDICION 1.-CONSTRUIR LA TABLA DE DISTRIBUCIÓN 1º Ordenamos los datos (ascendente) 50 60 64 66 72 53 61 64 66 73 54 61 64 67 74 55 62 64 67 75 2º Calculamos el Rango o Recorrido Total 57 62 65 68 76 57 63 65 68 77 58 63 65 70 78 58 64 65 70 79 R = X M − X m = 79 − 50 = 29 3º Calculamos la amplitud de cada clase o intervalo de clases i= R 29 = = 3.625 ≈ 4 nº de clases 8 (aumentemos el número de clases) La tabla de distribución de frecuencias Frecuencias Nº clases 8 7 6 5 4 3 2 1 Li 77,5 73,5 69,5 Clases 78-81 74-77 70-73 65,5 61,5 57,5 53,5 49,5 66-69 62-65 58-61 54-57 50-53 Ls 81,5 77,5 73,5 69,5 65,5 61,5 57,5 53,5 Pto Medio Xm. fi Xm Xm − X ( Xm − X ) 2 ( fi . Xm − X ) 2 fi 2 4 4 Fi 40 38 34 hr 0,050 0,100 0,100 hi(%) 5 10 10 Hi(%) 100 95 85 79,5 75,5 71,5 159 302 286 14,5 10,5 6,5 210,25 110,25 42,25 420,5 441 169 6 13 5 4 2 40 30 24 11 6 2 0,150 0,325 0,125 0,100 0,050 1,00 15 32,5 12,5 10 5 100 75 60 27,5 15 5 67,5 63,5 59,5 55,5 51,5 405 825,5 297,5 222 103 2600 2,5 -1,5 -5,5 -9,5 -13,5 6,25 2,25 30,25 90,25 182,25 37,5 29,25 151,25 361 364,5 1974 2.-CALCULAR LAS MEDIDAS DE TENDENCIA CENTRAL Medidas de tendencia central ∑ f .X i Media aritmética: x = Moda = Mo = Li + m n 2600 = = 65 40 Medidas de dispersión o variabilidad d1 .ic d1 + d 2 Desviación Tipica o estándar = s = De donde Li = 61.5 n − fi Mediana = Me = X d = Li + 2 .ic f d 2 = 13 − 6 = 7 s= ic = 4 De donde ( fi Xm − X 8 .4 = 8+7 32 = 61.5 + = 61.5 + 2.13 = 63.63 15 ∴ Mo = 63, 63 ≈ 64 Moda = Mo = 61.5 + n / 2 = 40 / 2 = 20 Li = 61.5 fi = 11 f = 13 ic = 4 ) Varianza : s 2 = n 2 1974 = 40 = n s = 7.02 ≈ 7 d1 = 13 − 5 = 8 ( fi Xm − X ( f i Xm − X n ) 2 = 1974 = 49.35 40 s 2 = 49.35 Coefiente de variación de Pearson: 20 − 11 .4 = 13 9 36 = 61.5 + .4 = 61.5 + = 61.5 + 2.77 = 64.27 13 13 ∴ X d = 64.27 ≈ 64 Al agrupar los datos en 8 intervalos de clases los valores de las medidas de tendencia central siguen siendo muy cercanos, con poca variabilidad Mediana = Me = X d = 61.5 + s 7 CV = .100 = .100 = 10, 77 ≈ 11% 65 x El priemer cuartil y el tercer cuatil vienen represntados por : Pk .n − fi X k = Li + 100 .ic f El cuartil 3 =El percentil75 El cuartil1= El percentil 25 Pk .n 75 3000 = .40 = = 30 100 100 100 Pk .n − fi 30 − 24 Q3 = X 75 = Li + 100 .ic = 65.5 + .4 = f 6 24 = 65.5 + = 65.5 + 4 = 69.5 ≈ 69 6 ∴ Q3 = X 75 = 69 En reumen tenemos. cuartil 1 Mediana cuartil 2 cuartil 3 Percentil 25 Percentil 50 Percentil 75 Pk .n − fi X k = Li + 100 .ic f Pk .n 25 1000 = = 10 .40 = 100 100 100 Pk .n − fi 10 − 6 .ic = 57.5 + .4 = Q1 = X 25 = Li + 100 5 f 16 = 57.5 + = 57.5 + 3.2 = 60.7 ≈ 60 5 ∴ Q1 = X 25 = 60 60 64 69 .4.- INTERPRETAR EN EL SEGUNDO INTERVALO LA FRECUENCIA ORDINARIA RELATIVA (h) Nº clases 2 Li 53,5 Clases 54-57 Ls 57,5 fi 4 Fi 6 hr 0,100 hi(%) 10 Hi(%) 15 Si tomamos aleatoria una muestra de dicha población obtenemos el 10 % de probabiliades de sacar un estudiante con notas de oscilen entre 54- 57 puntos, es decir, 4 estudiantes de los 40 en total 5.- INTERPRETAR EN EL CUARTO INTERVALO LA FRECUENCIA ACUMULADA RELATIVA (H) Nº clases 4 Li 61,5 Clases 62-65 Ls 65,5 fi 13 Fi 24 hr 0,325 hi(%) 32,5 Hi(%) 60 El 60% de los datos esta representado por el intervalo comprendido entre 62 y 65,es decir , 24 de los 40 estudiantes 6 -INDIQUE ELTIPO DE VARIABLE Y SU CORRESPONDIENTE ESCALA DE MEDICION La variable observada es de tipo cuantitativa (calificaciones ) y es discreta, ya que tomas valores enteros, la escala de medición es de razon o inetrvalos http://elimath.jimdo.com ) 2