que la mediana y el 50% de los valores son mayores o iguales que
Anuncio

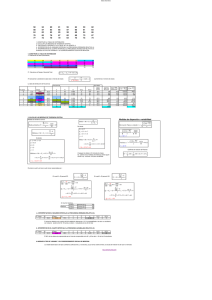
112 Capítulo 3 Estadísticos para describir, explorar y comparar datos que la mediana y el 50% de los valores son mayores o iguales que la mediana. Así como la mediana divide los datos en dos partes iguales, los tres cuartiles, denotados por Q1, Q2 y Q3, dividen los valores ordenados en cuatro partes iguales. (Los valores están ordenados cuando están acomodados en orden). He aquí las descripciones de los tres cuartiles: Q1 (primer cuartil): Separa el 25% inferior de los valores ordenados del 75% superior. (Para ser más precisos, al menos el 25% de los valores ordenados son menores o iguales que Q1, y al menos el 75% de los valores son mayores o iguales que Q1). Q2 (segundo cuartil): Igual a la mediana; separa el 50% inferior de los valores ordenados del 50% superior. Separa el 75% inferior de los valores ordenados del 25% Q3 (tercer cuartil): superior. (Para ser más precisos, al menos el 75% de los valores ordenados son menores o iguales que Q3, y al menos el 25% de los valores son mayores o iguales que Q3). Describiremos un procedimiento para el cálculo de cuartiles después de analizar los percentiles. No existe un acuerdo universal respecto de un procedimiento único para el cálculo de cuartiles; por esa razón, con frecuencia los distintos programas de cómputo producen resultados diferentes. Por ejemplo, si usted utiliza el conjunto de datos 1, 3, 6, 10, 15, 21, 28 y 36, obtendrá los siguientes resultados: STATDISK Minitab SPSS Excel SAS TI-83>84 Plus Q1 Q2 Q3 4.5 3.75 3.75 5.25 4.5 4.5 12.5 12.5 12.5 12.5 12.5 12.5 24.5 26.25 26.25 22.75 24.5 24.5 Si usted utiliza una calculadora o un programa de cómputo para resolver ejercicios que comprenden cuartiles, es posible que obtenga resultados que difieran ligeramente de las respuestas que vienen al final del libro. Así como existen tres cuartiles que separan un conjunto de datos en cuatro partes, también existen 99 percentiles, que se denotan P1, P2, c, P99, los cuales separan los datos en 100 grupos, con aproximadamente el 1% de los valores en cada grupo. (Los cuartiles y percentiles son ejemplos de cuantiles o fractiles, que separan los datos en grupos con aproximadamente el mismo número de valores). El proceso para calcular el percentil que corresponde a un valor x específico es bastante sencillo, tal como se indica en la siguiente expresión: Percentil del valor x 5 número de valores menores que x ? 100 número total de valores (el resultado se redondea al entero más cercano) EJEMPLO Edades de las mejores actrices La tabla 3-4 lista las 76 edades ordenadas de las mejores actrices ganadoras del Óscar que se incluyen en la tabla 2-1. (La tabla 2-1 aparece en el problema del capítulo 2). Calcule el percentil correspondiente a una edad de 30 años. 3-4 Tabla 3-4 Medidas de posición relativa Edades ordenadas de las 76 mejores actrices LA ESTADÍSTICA EN LAS NOTICIAS 21 22 24 24 25 25 25 25 26 26 26 26 27 27 27 27 28 28 28 28 29 29 29 29 29 29 30 30 31 31 31 32 32 33 33 33 33 33 34 34 34 35 35 35 35 35 35 35 36 37 37 38 38 38 38 39 39 40 41 41 41 41 41 42 42 43 45 46 49 50 54 60 61 63 74 80 SOLUCIÓN En la tabla 3-4 observamos que existen 26 edades menores que 30; por lo tanto, percentil de 30 5 26 ? 100 5 34 76 INTERPRETACIÓN La edad de 30 años es el percentil 34. El ejemplo anterior muestra cómo convertir un valor muestral dado a su percentil correspondiente. Existen diversos métodos para el procedimiento inverso de convertir un percentil en el valor correspondiente del conjunto de datos. El procedimiento que utilizamos se resume en la figura 3-6, que emplea la siguiente notación. Notación n k número total de valores en el conjunto de datos percentil utilizado (ejemplo: para el percentil 25, k 5 25) L localizador que da la posición de un valor (ejemplo: para el valor en el lugar 12 en la lista ordenada, L 5 12) Pk percentil k-ésimo (ejemplo: P25 es el percentil 25) EJEMPLO Edades de las mejores actrices Remítase a las edades ordenadas de las mejores actrices en la tabla 3-4 y utilice la figura 3-6 para calcular el valor del percentil 20, P20. Al consultar la figura 3-6, observamos que los datos muestrales ya están ordenados, de manera que podemos proceder a calcular el valor del localizador L. En este cálculo utilizamos k 5 20 porque estamos tratando de calcular el valor del percentil 20. Usamos n 5 76 porque tenemos 76 valores de datos. SOLUCIÓN L5 113 20 k ?n5 ? 76 5 15.2 100 100 continúa El crecimiento de la estadística El reportero Richard Rothstein escribió en el New York Times que el estudio del álgebra, la trigonometría y la geometría en preparatoria “dejan muy poco espacio para el estudio de la estadística y la probabilidad. No obstante, los estudiantes necesitan fundamentos sobre el análisis de datos”. El reportero indicó que el cálculo tiene un papel relevante en los estudios universitarios, a pesar de que “sólo pocos trabajos, principalmente en el campo técnico, realmente lo utilizan”. Rothstein citó un estudio realizado por el profesor Clifford Konold, de la Universidad de Massachusetts, en el cual se contó el número de presentaciones de datos en el New York Times. En los ejemplares del Times de 1972, el doctor Konold encontró cuatro gráficas o tablas en cada una de 10 ediciones de entre semana (sin incluir las secciones de deportes y negocios), pero en 1982 había 8 y en 1992 había 44; “al año siguiente él (el doctor Konold) encontró más de 100”. El crecimiento de la estadística como disciplina se ha visto fomentado, en parte, por un mayor uso de este tipo de presentaciones de datos en los medios de comunicación masiva. 114 Capítulo 3 Estadísticos para describir, explorar y comparar datos Inicio Start Ordenar los datos. (Acomodar los datos en orden, del menor al mayor). Calcular L 5 k n donde 100 n 5 número de valores k 5 percentil en cuestión ( ( ¿L es un número entero? Sí No El valor del k-ésimo percentil está la mitad entre el L-ésimo valor y el siguiente valor en el conjunto ordenado de datos. Obtenga Pk sumando el L-ésimo valor y el siguiente valor, y luego dividiendo el total entre 2. Modifique L redondeando al siguiente entero más grande. No El valor de Pk es el L-ésimo valor, contando a partir del más bajo. Figura 3-6 Conversión del k-ésimo percentil al valor del dato correspondiente NDespués, nos preguntamos si L es un número entero. La respuesta es no, por lo que procedemos al siguiente recuadro inferior, donde modificamos L redondeando su valor al entero más alto, de 15.2 a 16. (En este libro generalmente redondeamos de la forma acostumbrada, pero éste es uno de los dos casos en que redondeamos hacia arriba en vez de redondear hacia el entero más cercano). Por último, el recuadro inferior muestra que el valor de P20 es el decimosexto valor, contando del más bajo al más alto. En la tabla 3-4 el valor 16º es 27. Es decir, P20 5 27 años de edad. EJEMPLO Edades de las mejores actrices Remítase a las edades de las mejores actrices en la tabla 3-4. Utilice la figura 3-6 para calcular el valor de Q3, que es el tercer cuartil. 3-4 Medidas de posición relativa 115 SOLUCIÓN Primero señalamos que Q3 es igual a P75, de manera que procedemos con el objetivo de calcular el valor del percentil 75. Si nos remitimos a la figura 3-6, observamos que los datos de la muestra ya están ordenados, así que procedemos a calcular el valor del localizador L. Para este cálculo utilizamos k 5 75, ya que estamos tratando de obtener el valor del percentil 75, y usamos n 5 76 porque son 76 valores de datos. L5 75 k ?n5 ? 76 5 57 100 100 Luego, nos preguntamos si L es un número entero y respondemos que sí, de manera que vamos al siguiente recuadro a la derecha. Ahora podemos ver que el valor del percentil k-ésimo (75º) se encuentra a la mitad entre el valor L-ésimo (57º) y el siguiente valor del conjunto original de datos. Es decir, el valor del percentil 75 se encuentra a la mitad entre el quincuagésimo séptimo valor (57º) y el quincuagésimo octavo valor (58º). El valor 57º es 39 años y el valor 58º es 40 años; por lo tanto, el valor a la mitad de ellos es 39.5 años. Concluimos que el percentil 75 es P75 5 39.5 años. El valor del tercer cuartil Q3 también es de 39.5 años. El ejemplo anterior demuestra que al calcular un valor cuartilar (como Q3), es posible utilizar el valor del percentil equivalente (como P75) en su lugar. Al margen se indican las relaciones equivalentes entre cuartiles y percentiles. En secciones anteriores de este capítulo, describimos diversos estadísticos, incluyendo media, mediana, moda, rango y desviación estándar. Algunos otros estadísticos se definen con el uso de cuartiles y percentiles, como los siguientes: rango intercuartilar (o RIC) 5 Q3 2 Q1 rango semiintercuartilar 5 Q3 2 Q1 2 cuartil medio 5 Q3 1 Q1 2 rango de percentiles 10-90 5 P90 2 P10 Después de completar esta sección, usted podrá convertir un valor en su puntuación z (o puntuación estándar) correspondiente, de forma que sea posible compararlo con otros valores que provienen de diferentes conjuntos de datos. También podrá convertir un valor en su valor percentilar correspondiente, de manera que pueda compararlo con otros valores en algún conjunto de datos. También sabrá convertir un percentil en su valor de dato correspondiente. Finalmente, comprenderá el significado de los cuartiles y podrá relacionarlos con sus valores percentiles correspondientes (como en Q3 5 P75). Q 1 5 P25 Q 2 5 P50 Q 3 5 P75