feb 07 sol

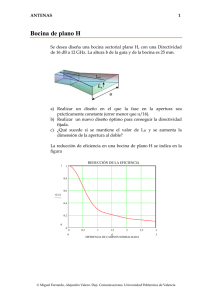
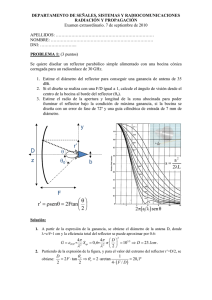
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 30 ENERO 2007
APELLIDOS, NOMBRE: ………………………………………………………… DNI: …………..
PROBLEMA: (1 hora) (50% de la nota)
Se pretende hacer un primer análisis de un posible radioenlace a 10 GHz para comunicar las dos orillas de un
lago, separadas 10 km, utilizando como antenas dos reflectores offset iguales, como el de la figura, de 40 cm de
diámetro de apertura. Se dispone de un amplificador de bajo ruido que hace que la temperatura de ruido del
receptor sea de 100K. El ancho de banda del sistema es de 2MHz.
1. Con el haz horizontal, la temperatura de ruido de la antena receptora se estima en 200K. Calcule la
potencia mínima disponible a la entrada del receptor para obtener una relación S/N = 30 dB. (k=1.38 10-23
W/Hz/K) (2p)
2. Diseñe una bocina cónica corrugada (radio a, altura de bocina H, y profundidad de corrugaciones d) de
bajo error de fase (s=0.2), para conseguir un nivel de iluminación en el borde (propio de la bocina) de –10
dB. (2p)
3. A partir de los anchos de haz a –3dB, estime la directividad de la bocina y su eficiencia de apertura
(1p)
4. Estime la ganancia de los reflectores parabólicos. (1p)
5. Calcule la altura mínima de las dos torres de antena para conseguir una interferencia constructiva en el
radioenlace. (1p)
6. En las condiciones anteriores, calcule la potencia mínima que debe entregar el transmisor a su antena. (2p)
7. Si hay una densidad de lluvia en el trayecto de 25 mm/hora, estime en cuánto se reduce la relación S/N
(1p)
d
a
40 cm
2 cm
2ψ s
zf
H
ψs = 20º
Diagrama universal de la bocina cónica corrugada
Atenuación por lluvia(dB/km)
SOLUCIÓN DEL EXAMEN:
1. Para el cálculo de la potencia mínima, calculamos el ruido y consideramos la S/N deseada:
PDR min
S PDR min
=
=
⇒ PDR min = 8.28 ⋅ 10 −12 W ⇔ −80.8dBm
N
kTB
k (Ta + Teq ,rx )B
2. Diseño de la bocina: para el cálculo del radio se va a la gráfica (s=0.2) con un valor de ordenadas
de 0.316 correspondiente a –10 dB. En abcisas se obtiene 3.8, valor que corresponde a θ=ψs=20º:
2πa
3.8 =
sin 20º ⇒ a = 5.3cm
λ
a2
A partir de este valor, L =
= 23.4cm . Por semejanza de triángulos se obtiene H, del modo:
2λs
L
H = L−
⋅ 1.0 = 19cm
5.3
El valor de la profundidad de las corrugaciones es del orden de λ/4 = 7.5 mm para cancelar las
corrientes longitudinales en la pared interior de la bocina
3. Directividad y eficiencia de apertura de la bocina. En la gráfica de la bocina, para s=0.2 y
ordenada = 0.707 (-3 dB), se obtiene una abcisa de 2.35:
2.35 =
2 π ⋅ 5 .3
4π
sin θ −3dB ⇒ θ −3dB = 12.2º = 0.21rad ⇒ BW−3dB = 0.42 rad ⇒ D o =
= 69 ⇔ 18.4dBi
λ
0.42 2
Para el cálculo de la eficiencia de apertura, se tiene :
D o = 4π
A boc
ε ap ⇒ ε ap = 0.56
λ2
4. Directividad del reflector, estimando la eficiencia global del reflector offset en 0.7:
D o = 4π
A ref
ε g = 1228 .2 ⇒ 30.9dBi
λ2
5. Altura de las antenas. Haciendo las alturas iguales, para que el rayo directo y el rayo reflejado se
sumen en fase, es necesario que el camino a través del punto de reflexión sea λ/2 mayor que el
camino directo, puesto que el coeficiente de reflexión es igual a –1.
10000 2 + 4h r − 10000 = 0.015 ⇒ h r = 8.66 m
2
6. Aplicando la fórmula de Friis corregida con el factor de potencia asociada a la reflexión
(Fp=4=6dB), se tiene, teniendo en cuenta que GT = GR = Do = 30.9 dBi:
PDR , min
PDT
2
⎛ λ ⎞
⎟⎟ ⋅ G T ⋅ G R ⋅ Fp ⇒ PDT = −16.2dBm (0.024 mW )
= ⎜⎜
⎝ 4πR 1 ⎠
7. La lluvia reduce la señal en 10 km x 0.6 dB/km = 6 dB. Como mínimo la relación S/N se reduce
en el mismo valor. Para obtener un valor más exacto debe tenerse en cuenta que para una
trayectoria horizontal Ta tiende a 290K, lo que daría una relación:
S
290 + 100
= 30 − 6 − 10 log
= 22.9dB ⇒ Reducción de 7.1 dB
N
200 + 100
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 30 ENERO 2007
APELLIDOS, NOMBRE: ………………………………………………………… DNI: …………..
TEORÍA: (30 minutos) (50% de la nota)
Instrucciones: responda de manera breve y concisa, en el espacio asignado, a cada pregunta. No es necesario realizar ningún
cálculo (deje las operaciones indicadas) por lo que no está permitido utilizar calculadora.
1. ¿Por qué no se produce zona de sombra a 3 MHz en torno a una antena de HF? (0.5p)
Porque la frecuencia es inferior a la frecuencia crítica de la capa F2.
2. Como usted sabe, la máxima frecuencia que retorna a Tierra en comunicaciones ionosféricas cumple la
ley de la secante: MUF = f c ⋅ sec φo ¿Cuál es la causa de que las ondas por encima de alrededor de 30
MHz no retornen a Tierra? (0.5p)
Porque el rayo límite rasante con la curvatura de la Tierra da un ángulo de incidencia en torno a
75º , lo que hace que la MUF sea en cualquier caso inferior a 30 MHz.
3. Para un sistema de radiodifusión en onda media por onda de superficie (1 MHz) se emplea una antena
parabólica iluminada por un dipolo horizontal situado en su foco... Señale las dos incongruencias que hay
en la frase anterior. (0.5p)
En onda de superficie no se puede utilizar polarización horizontal.
A 1 MHz no se puede utilizar un reflector ya que sus dimensiones deben ser de varias longitudes de
onda.
4. A partir de qué frecuencia puede ser importante la atenuación por lluvia. (0.5p)
A partir de 3 GHz (depende de la intensidad de lluvia)
5. ¿Cuál es el margen de temperaturas típicas de antenas de estaciones terrenas de comunicaciones por
satélite en banda X (8 GHz)? (0.5p)
En torno a 40-100K
6. ¿Qué ganancia típica se puede obtener con una Yagi de 3 elementos? (0.5p)
En torno a 9 dBi
7. ¿Cuál es la misión de las varillas radiales que se colocan en la base de los mástiles radiantes de
radiodifusión en onda media? (0.5p)
Mejorar la conductividad de la tierra para reducir las pérdidas (mejorar el rendimiento de
radiación)
8. ¿Qué condiciones debe cumplir la geometría de una hélice para radiar en el modo axial? (0.5p)
El perímetro del cilindro en el que se enrolla debe tener una longitud del orden de una longitud de
onda, y el ángulo de ataque debe ser de 12º a 15º (paso de 0.25λ)
9. Si se diseña un array con una excitación que reduce el nivel de lóbulos secundarios respecto al caso de
iluminación uniforme, ¿qué ocurre con la directividad y la anchura de haz entre puntos de potencia mitad?
(0.5p)
El ancho de haz aumenta y la directividad disminuye
10. Para un array endfire, ¿qué separación típica máxima entre elementos se puede utilizar para que no
aparezca un fuerte lóbulo trasero (grating lobe)? (0.5p)
Inferior a 0.5λ. Los valores típicos son de 0.4 a 0.45λ
11. ¿Cuál es el significado del término “bocina óptima”? (0.5p)
Es la que consigue una longitud mínima para una ganancia dada.
12. ¿Por qué son diferentes las anchuras del lóbulo principal en los planos principales de una bocina cónica
lisa? (0.5p)
Porque las leyes de iluminación en amplitud de la boca de la bocina tienen distinto tappering en el
plano E y en el plano H.
13. Diga qué ocurre a la ganancia, eficiencias, ancho de haz y nivel de lóbulo lateral, cuando a un reflector
de primer foco iluminado para máxima ganancia se le sustituye el alimentador por otro de mayor
ganancia. (1p)
La ganancia disminuye (por partir de un punto óptimo), la eficiencia de spillover mejora, pero
empeora la eficiencia de apertura, dando lugar a la pérdida de ganancia anterior. La anchura de
haz aumenta y el nivel de lóbulos secundarios se reduce porque la bocina de mayor ganancia
ilumina con un tappering más acusado el borde del reflector.
14. Una antena que funciona a 3 GHz genera un campo radiante de 1V/m a 1 metro de distancia en la
dirección de máxima radiación, cuando se le entrega una potencia de 1mW.
a) Escriba la fórmula y la expresión numérica de la amplitud compleja del campo eléctrico a 6
metros de distancia. (0.5p)
E=
E(1m ) − jk o ∆r 1
⋅e
= V / m . La fase es 0 tanto a 1 metro como a 6 metros ya que λ=0.1m.
r (m)
6
b) Escriba la fórmula y la expresión numérica de la densidad de potencia a 100 metros de distancia.
(0.5p)
S =
E(100m )
2η o
2
=
(1 / 100)2 W / m 2
240π
c) Escriba la fórmula y la expresión numérica de la ganancia de la antena. (0.5p)
G=
4πr 2 S
Prad
=
4π100 2 S
10 −3
3 ⋅ e − jk o z
(2x̂ + ŷ ) , incide
z
proveniente de un punto lejano situado sobre el eje de las z positivas, un campo de 0.1x̂ V/m. La
15. Sobre una antena que en transmisión radia en la dirección del eje z un campo
directividad de la antena en la dirección del eje z es de 10 dBi y funciona a una frecuencia de 3 GHz
a) Escriba las expresiones de los vectores unitarios de polarización y del factor de desacoplo de
polarización. (0.5p)
2
2x̂ + ŷ
; ê R = x̂
ê T =
5
FPP = ê T ⋅ ê R
2
2 x̂ + ŷ
=
⋅ x̂ = 4 / 5
5
b) Escriba la fórmula (fórmulas) y expresión numérica de la potencia disponible en bornes de la
antena. (1p)
PDR = ê T ⋅ ê R ⋅ Sinc A e = ê T ⋅ ê R ⋅ Sinc
2
2
λ2
4 0.12 0.12
⋅
Do = ⋅
10
4π
5 240π 4π