sol EX sept2010
Anuncio
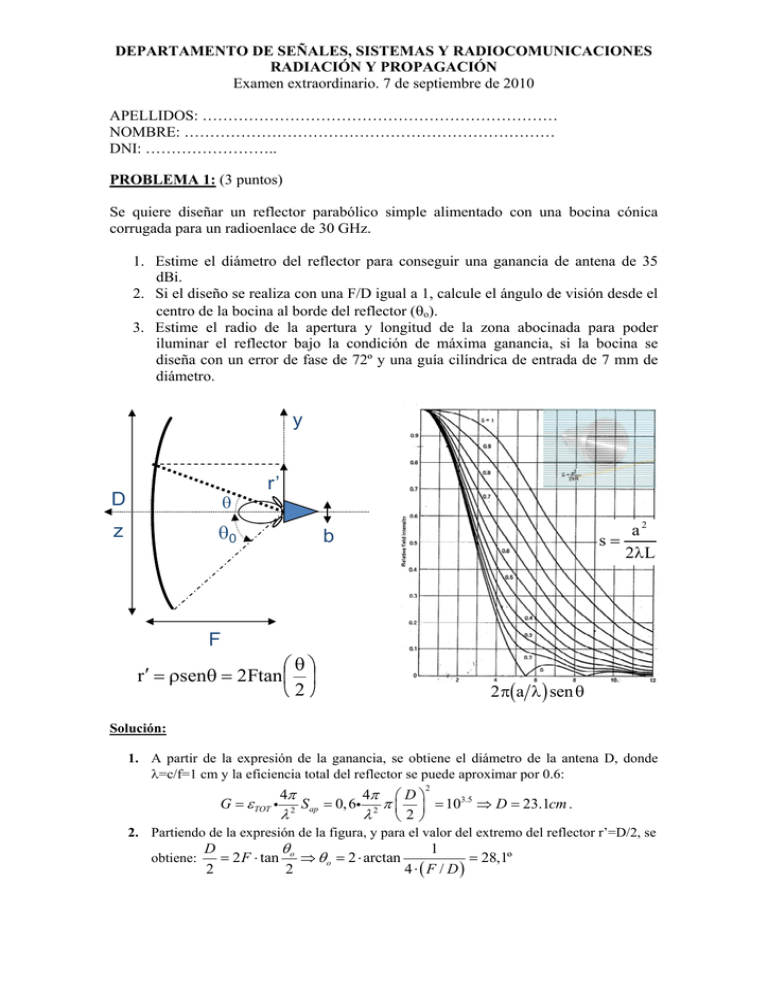
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES RADIACIÓN Y PROPAGACIÓN Examen extraordinario. 7 de septiembre de 2010 APELLIDOS: …………………………………………………………… NOMBRE: ……………………………………………………………… DNI: …………………….. PROBLEMA 1: (3 puntos) Se quiere diseñar un reflector parabólico simple alimentado con una bocina cónica corrugada para un radioenlace de 30 GHz. 1. Estime el diámetro del reflector para conseguir una ganancia de antena de 35 dBi. 2. Si el diseño se realiza con una F/D igual a 1, calcule el ángulo de visión desde el centro de la bocina al borde del reflector (o). 3. Estime el radio de la apertura y longitud de la zona abocinada para poder iluminar el reflector bajo la condición de máxima ganancia, si la bocina se diseña con un error de fase de 72º y una guía cilíndrica de entrada de 7 mm de diámetro. y D z 0 r’ a2 s 2 L b F r sen 2Ftan 2 2a sen Solución: 1. A partir de la expresión de la ganancia, se obtiene el diámetro de la antena D, donde =c/f=1 cm y la eficiencia total del reflector se puede aproximar por 0.6: 4 4 2 D G TOT 2 Sap 0, 6 2 103.5 D 23.1cm . 2 2. Partiendo de la expresión de la figura, y para el valor del extremo del reflector r’=D/2, se obtiene: D 1 2 F tan o o 2 arctan 28,1º 2 2 4 F / D 3. Para el error de fase de la bocina: s 72º 0, 2 y con un nivel en el extremo del 360º reflector de -10 dB = 0,32 (excitación óptima), vamos a la gráfica de la bocina con a =o=28,1º, y se obtiene 2 obtener s Labocinada, 2 primero sin o 3, 7 . Despejando el valor de a: a=1,25 cm. Para calculamos el valor de L, a partir de: 2 a a L 3,91cm . El valor de Labocinada se obtiene resolviendo el triángulo 2 L 2 s de la figura: Laboc 39,1 3,5 39,1 28, 2mm 12,5 PROBLEMA 2: (2 puntos) Una antena Cassegrain de 3 metros de diámetro bien diseñada y construida, se utiliza como estación terrena de un enlace de comunicaciones de datos en banda C (6 GHz) con el Satélite Hispasat Amazonas (en órbita geostacionaria a 36000 km). 1. Si la PIRE del satélite en la dirección del enlace es de 45 dBW, ¿cuánto vale la potencia disponible en bornes de la antena de la estación terrena? 2. Haga una estimación de la relación señal a ruido si la banda de frecuencia intermedia necesaria para el enlace es de 2 MHz y la figura de ruido del receptor es de 2 dB. (k=1.38 10-23 J/K) Solución: 1. La potencia disponible 2 Pdis S Aeq la calculamos a partir de la expresión: 2 PIRE 10 mW D 3 tot 0, 7 10 log10 Pdis 80,17dBm 2 2 4 r 4 36000000 2 2 7,5 2. Para el cálculo del ruido, estimamos la temperatura de ruido de antena en 20K, y para un ancho de banda de ruido de 2MHz, obtenemos: N 10 log10 kTB 10 log10 k Ta To( f 1) B 112,8dBm , donde To=290K y f=100,2 Por lo tanto, la relación Señal a Ruido será: S/N (dB) = S(dBm) – N(dBm) = 32,6 dB DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES EXAMEN DE RADIACIÓN Y PROPAGACIÓN Examen extraordinario. 7 de septiembre de 2010 TEORÍA (5 puntos) 1. En propagación por onda ionosférica, explique qué es la frecuencia óptima de trabajo y de qué depende. Explique por qué esta frecuencia varía a lo largo de las horas del día. (1p) La frecuencia óptima de trabajo se corresponde al 85% de la MUF (máxima frecuencia utilizable), con lo que depende de la frecuencia crítica y del ángulo de incidencia en la ionosfera para el enlace. No conviene que sea más alta para evitar que no se refleje el rayo en la ionosfera ni más baja para minimizar la atenuación. Varía a lo largo de las horas del día porque lo hace la frecuencia crítica. 2. ¿Diga cómo orientaría un dipolo resonante receptor (con respecto a x, y, z) para recibir la máxima potencia de una onda incidente cuyo campo eléctrico, en amplitud compleja, vale: E z xˆ 3 yˆ exp j10 z - con z en metros-? ¿Qué dimensiones tendría el dipolo anterior? (1p) Dado que la polarización de la onda es lineal, al igual que la del dipolo, éste se colocaría para maximizar la potencia recibida (anular las pérdidas por desacoplo de polarización). Esto significa que se tiene que situar paralelo a la polarización de la onda recibida: atan(3/1)=71º respecto del eje x. Para calcular la longitud, sabemos que el dipolo es resonante, luego su longitud será aproximadamente 0,47, donde la obtenemos de la constante de propagación: ko 2 10 0, 2m L 0, 47 9, 4cm 3. ¿Qué haría para orientar el máximo de radiación hacia la dirección =0º (respecto a z) de un array lineal a 6 GHz de 10 elementos equiespaciados y separados 2 cm situados sobre el eje z? ¿Qué pasaría si la separación entre elementos fuera de 2.5cm? (1p) Para ello hay que ajustar las fases de los elementos del array de modo que tengan el máximo orientado hacia 0º, mediante el siguiente salto de fase entre elementos: ko d cos 0º 0 360º 2cm 144º . Si la separación entre elementos fuera de 2.5 5cm cm, es decir media longitud de onda, aparecería otro lóbulo de igual nivel (en el caso en el que los elementos radiantes tuvieran radiación isótropa) en =180º. 4. Una antena Yagi de 15 dBi de ganancia presenta una impedancia de entrada de 50+j20 ohmios y un rendimiento de radiación de 0.85. Si la antena anterior se conecta a un transmisor de 1W de potencia disponible y de 50 ohmios de impedancia de salida, ¿cuánto vale la potencia entregada a la antena, la reflejada hacia el transmisor y la potencia radiada por la antena? (1p) La potencia entregada a la antena la calculamos a partir de Pet Pdt 1 T coeficiente de reflexión se calcula como: T 2 , donde el Z ant Z tx* 0, 2 . Con este valor de Z ant Z tx coeficiente de reflexión, la potencia entregada a la antena valdría Pet=0,96W. La potencia reflejada (1W-0,96W) es Pref = 0,04W. Por último la potencia radiada se calcula como: Prad rad Pet 0,82W 5. ¿Qué densidad de potencia produce la antena del apartado anterior en la dirección de máxima radiación, a una distancia de 10 km? (1p) La densidad de potencia se calcula a partir de la expresión: 15/10 P G 0,96 10 S et 2ant 10 log10 S 46, 2dB 1mW / m 2 4 r 4 100002