Curso 06/07 (Segundo Parcial)
Anuncio

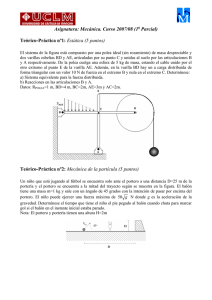
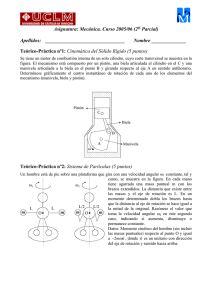
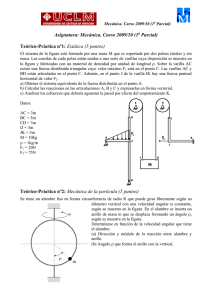
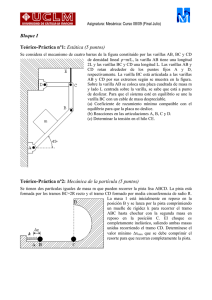
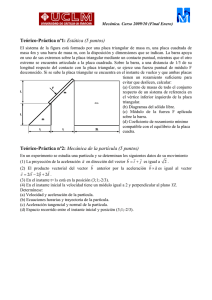
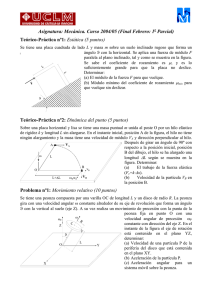
Asignatura: Mecánica. Curso 2006/07 (2o Parcial) Teórico-Práctica nº1: Sistemas de referencia no inerciales (5 puntos) Se tiene una plataforma circular de radio R=2 m que está girando en un determinado instante con un velocidad angular ω=2 rad/s en sentido antihorario está acelerando con una aceleración de módulo α=1 rad/s2. Sobre la plataforma existe una rampa con una acanaladura que forma un ángulo de 45º con la horizontal, las paredes de la rampa son lisas y el suelo tiene un coeficiente de rozamiento dinámico µ=0.1. Por la rampa desciende deslizando una partícula de masa m=20 kg y diámetro coincidente con la anchura de la acanaladura con una velocidad v respecto a la rampa. Cuando la bola ha descendido la mitad de la rampa tiene una velocidad de módulo 2 m/s, determínese: (a) Módulo, dirección y sentido de todas las fuerzas sobre la bola para un observador sobre la plataforma (sistema xyz). (b) Dibújese sobre el la figura la diversas fuerzas sobre la bola. Teórico-Práctica nº2: Sistemas de partículas (5 puntos) Se tiene un sistema compuesto por dos masas puntuales unidas a una varilla ABC de masa despreciable con forma de escuadra de longitud 2L (AB=BC=L). En la posición C está unida la partícula de masa m y en el punto B la 2m. En la posición inicial el sistema está en reposo con el punto C de la escuadra en la vertical con la articulación (posición A), según se muestra en la figura. Si en este instante se libera el sistema obténgase: a) Aceleración angular en función del ángulo ϕ que forma el segmento de la varilla AB con la horizontal (Escribir la ecuación diferencial). b) Velocidad angular de la varilla cuando la varilla AB ha girado un ángulo de 135º. Problema nº1: Dinámica del Sólido Rígido (10 puntos) Se tiene un cubo de masa m=100 kg y lado L=1 m soldado por unos de sus lados a un eje de masa despreciable que gira con una velocidad angular constante ω=10 rad/s apoyada en dos rodamientos montados a una distancia L/2 del extremo del cubo, tal y como se muestra en la figura. En un instante un motor comienza a acelerar el conjunto con una aceleración α=1 rad/s2. Determínese en el instante de la figura: (a) Tensor de inercia en el punto B. (b) Par y potencia del motor para realizar este movimiento. (c) Reacciones en los apoyos. A y B.