Curso 05/06 (Convocatoria de Junio)
Anuncio
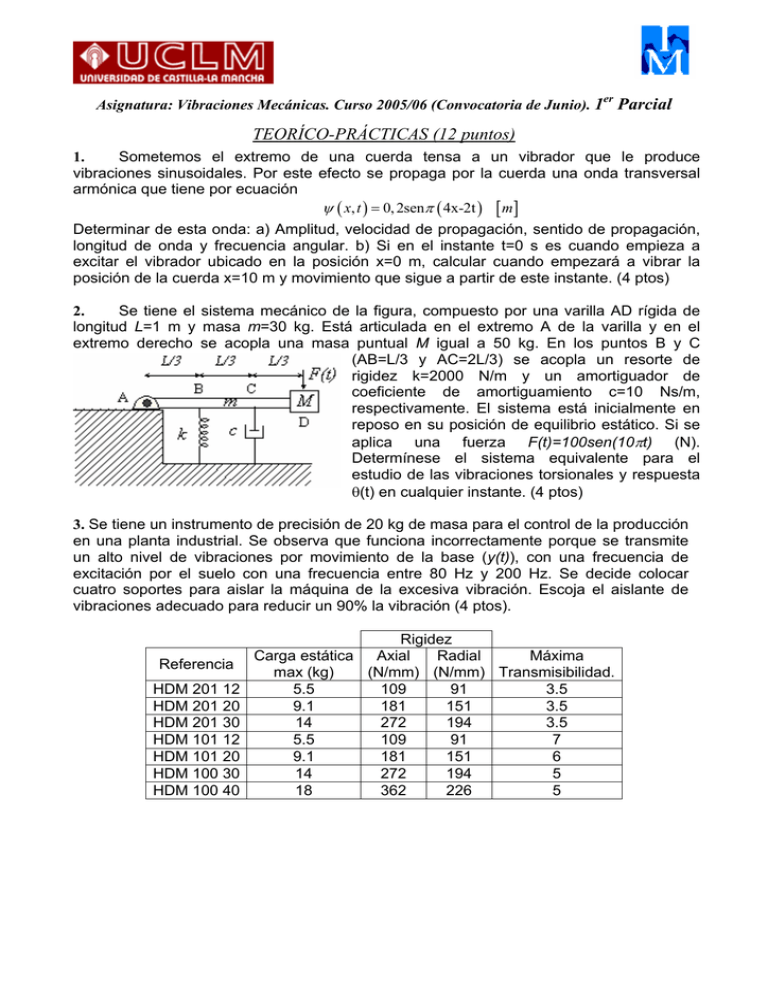
er Asignatura: Vibraciones Mecánicas. Curso 2005/06 (Convocatoria de Junio). 1 Parcial TEORÍCO-PRÁCTICAS (12 puntos) 1. Sometemos el extremo de una cuerda tensa a un vibrador que le produce vibraciones sinusoidales. Por este efecto se propaga por la cuerda una onda transversal armónica que tiene por ecuación ψ ( x, t ) = 0, 2senπ ( 4x-2t ) [ m ] Determinar de esta onda: a) Amplitud, velocidad de propagación, sentido de propagación, longitud de onda y frecuencia angular. b) Si en el instante t=0 s es cuando empieza a excitar el vibrador ubicado en la posición x=0 m, calcular cuando empezará a vibrar la posición de la cuerda x=10 m y movimiento que sigue a partir de este instante. (4 ptos) 2. Se tiene el sistema mecánico de la figura, compuesto por una varilla AD rígida de longitud L=1 m y masa m=30 kg. Está articulada en el extremo A de la varilla y en el extremo derecho se acopla una masa puntual M igual a 50 kg. En los puntos B y C (AB=L/3 y AC=2L/3) se acopla un resorte de rigidez k=2000 N/m y un amortiguador de coeficiente de amortiguamiento c=10 Ns/m, respectivamente. El sistema está inicialmente en reposo en su posición de equilibrio estático. Si se aplica una fuerza F(t)=100sen(10πt) (N). Determínese el sistema equivalente para el estudio de las vibraciones torsionales y respuesta θ(t) en cualquier instante. (4 ptos) 3. Se tiene un instrumento de precisión de 20 kg de masa para el control de la producción en una planta industrial. Se observa que funciona incorrectamente porque se transmite un alto nivel de vibraciones por movimiento de la base (y(t)), con una frecuencia de excitación por el suelo con una frecuencia entre 80 Hz y 200 Hz. Se decide colocar cuatro soportes para aislar la máquina de la excesiva vibración. Escoja el aislante de vibraciones adecuado para reducir un 90% la vibración (4 ptos). Referencia HDM 201 12 HDM 201 20 HDM 201 30 HDM 101 12 HDM 101 20 HDM 100 30 HDM 100 40 Rigidez Carga estática Axial Radial Máxima max (kg) (N/mm) (N/mm) Transmisibilidad. 5.5 109 91 3.5 9.1 181 151 3.5 14 272 194 3.5 5.5 109 91 7 9.1 181 151 6 14 272 194 5 18 362 226 5 PROBLEMA (8 Puntos) Se tiene un conjunto de una cremallera con un piñón, la masa de la cremallera es M y la del piñón m, iguales a 10 kg. El radio primitivo del piñón es R=20 cm y el momento de inercia respecto a su eje es I0=mR2/2, el piñón puede únicamente girar libremente en torno de su eje. Si la cremallera está unida a una pared que se puede desplazar paralelamente por medio de un actuador hidráulico con un muelle de rigidez k=200 N/m. Determínese: (a) Sistema equivalente para estudiar las vibraciones de la cremallera. (b) La frecuencia de vibración del sistema cremallera-piñón. (c) Si el actuador está en reposo y se desplaza la cremallera un distancia x0=20 cm y se libera, obtener la respuesta del sistema. (d) El actuador comienza a desplazar la pared siguiendo un movimiento armónico simple de ecuación y(t)=0.1⋅sen(2πt) (cm) con el sistema cremallera-piñón inicialmente en reposo, determinar la respuesta del sistema. er Asignatura: Vibraciones Mecánicas. Curso 2005/06 (Convocatoria de Junio). 2 Parcial TEORÍCO-PRÁCTICAS (12 puntos) 1. Se tiene el sistema mecánico de la figura, compuesto por un carretón de masa m, unido a una pared por medio de un resorte de rigidez k y un amortiguador viscoso de coeficiente de amortiguamiento c. El sistema no tiene resistencia a la rodadura y tiene amortiguamiento subcrítico. El sistema está inicialmente en reposo en su posición de equilibrio estático. Si se aplica una fuerza consistente en una delta de Dirac igual a F(t)=I⋅δ(t), donde I es el impulso igual a F0∆t. a) ¿Cómo se obtendría la respuesta en el dominio de la frecuencia?. b) ¿Cómo se calcularía la respuesta en el dominio del tiempo a partir de la respuesta en el dominio de la frecuencia?. (6 ptos) 2. Se tiene un disco de masa M y radio R sobre una pista de hielo. El disco tiene un eje de rotación en el centro de masas. En el eje del disco se acopla un resorte de rigidez k y en la periferia del disco, en el diámetro correspondiente al punto de apoyo en la posición de equilibrio estático, otro resorte de rigidez 2k, tal y como se muestra en la figura. Obténgase las ecuaciones dinámicas del sistema por el método de Lagrange para estudiar las vibraciones del disco en ausencia de excitaciones exteriores. 1 I Disco = MR 2 2 PROBLEMA (6 Puntos) Se tiene un edificio de dos plantas como el que se muestra en la figura. En cada planta tiene seis pilares iguales de acero con un módulo de Young 210 GPa y sección cuadrada de 20 cm de lado fabricadas con un espesor de 1 cm. Los forjados son losas de hormigón que se consideran infinitamente rígidas en su plano y a flexión, con una densidad de 2500 kg/m3. Cada planta tiene una anchura de 10 m, longitud 20 m y espesor 20 cm. Determínese: (a) Número de grados de libertad y sistema equivalente para estudiar las vibraciones de flexión de cada una de las plantas del edificio. (b) Frecuencias naturales. (c) Modos de vibración. 12 EI y momento de inercia polar L3 h·(25·b3 - 54·b 2 ·h +44·b·h 2 -8 h 3 ) de la viga. I = 48 Rigidez equivalente del pilar: K P = PROBLEMA (6 Puntos) En una instalación industrial se tiene una máquina compuesta por un motor eléctrico, reductor y compresor. Se observa que la máquina tiene un nivel anormalmente alto de vibraciones con una pérdida de rendimiento. Para detectar la causa del problema se efectúa un análisis en frecuencia midiendo la vibración sobre el reductor en dirección vertical. En función de los datos constructivos, razonar justificadamente cuáles son los defectos que sufre la máquina. Características técnicas Datos del reductor: Datos del motor: Potencia: 10kW Velocidad en medición: 1500 rpm Número de pares de polos: 2 Rodamientos tipo 1 en todos los apoyos Eje de entrada con rueda 15 dientes Eje intermedio con 26 dientes (entrada) Eje intermedio con 15 dientes (salida) Eje de salida con rueda 26 dientes Datos del compresor: Rodamientos de la máquina (Tipo 1): Número de álabes: 24 Rodamientos tipo 1 Diámetro de bolas: 16 mm Número de bolas: 13 Diámetro pista interior: 56 mm Diámetro pista exterior: 72 mm Angulo de contacto: 0º 1.8 1.6 Vibración (mm/s) 1.4 1.2 1.0 0.8 0.6 0.4 0.2 0.0 0 25 50 75 100 125 150 Frecuencia (Hz) 175 200 225 250