Curso 05/06 (Primer Parcial)
Anuncio
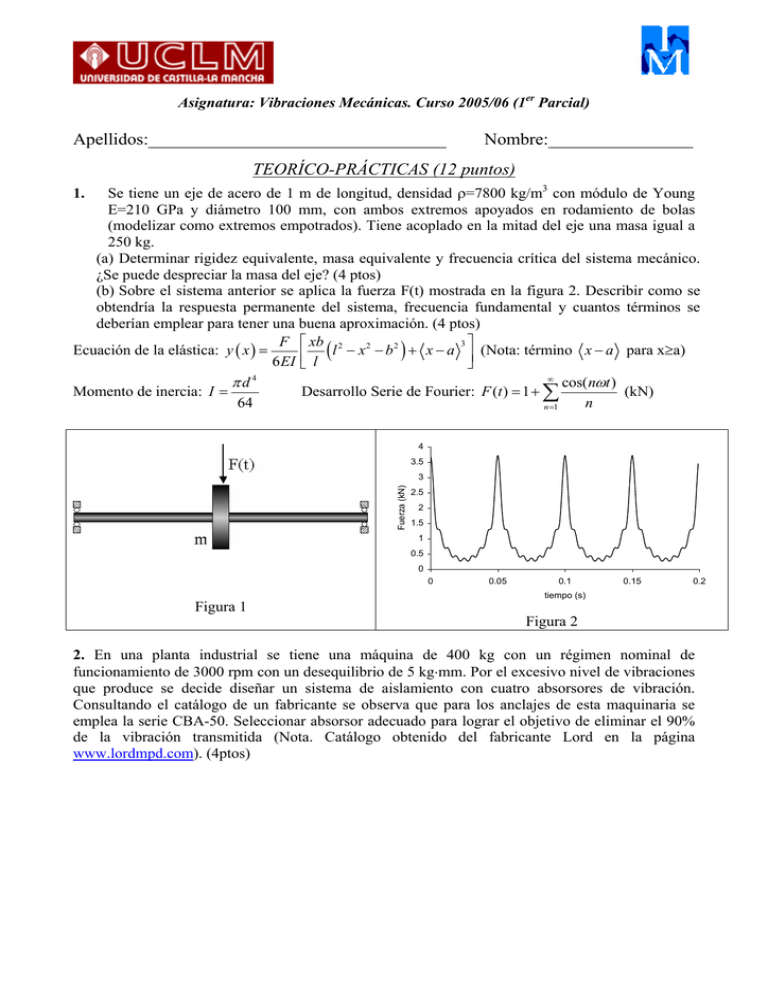
Asignatura: Vibraciones Mecánicas. Curso 2005/06 (1er Parcial) Apellidos:_________________________________ Nombre:________________ TEORÍCO-PRÁCTICAS (12 puntos) Se tiene un eje de acero de 1 m de longitud, densidad ρ=7800 kg/m3 con módulo de Young E=210 GPa y diámetro 100 mm, con ambos extremos apoyados en rodamiento de bolas (modelizar como extremos empotrados). Tiene acoplado en la mitad del eje una masa igual a 250 kg. (a) Determinar rigidez equivalente, masa equivalente y frecuencia crítica del sistema mecánico. ¿Se puede despreciar la masa del eje? (4 ptos) (b) Sobre el sistema anterior se aplica la fuerza F(t) mostrada en la figura 2. Describir como se obtendría la respuesta permanente del sistema, frecuencia fundamental y cuantos términos se deberían emplear para tener una buena aproximación. (4 ptos) F xb 2 3 l − x 2 − b 2 ) + x − a (Nota: término x − a para x≥a) Ecuación de la elástica: y ( x ) = ( 6 EI l 4 ∞ cos(nωt ) πd Desarrollo Serie de Fourier: F (t ) = 1 + ∑ (kN) Momento de inercia: I = n 64 n =1 1. 4 3.5 Fuerza (kN) 3 2.5 2 1.5 1 0.5 0 0 Figura 1 0.05 0.1 0.15 0.2 tiempo (s) Figura 2 2. En una planta industrial se tiene una máquina de 400 kg con un régimen nominal de funcionamiento de 3000 rpm con un desequilibrio de 5 kg⋅mm. Por el excesivo nivel de vibraciones que produce se decide diseñar un sistema de aislamiento con cuatro absorsores de vibración. Consultando el catálogo de un fabricante se observa que para los anclajes de esta maquinaria se emplea la serie CBA-50. Seleccionar absorsor adecuado para lograr el objetivo de eliminar el 90% de la vibración transmitida (Nota. Catálogo obtenido del fabricante Lord en la página www.lordmpd.com). (4ptos) PROBLEMA (8 Puntos) Se tiene una varilla rígida esbelta de longitud 2L con L=2 m y masa 3m con m=100 kg, articulada en la mitad con un resorte de rigidez torsional KT=1000 N⋅m, tal y como, se muestra en la figura. En el extremo izquierdo tiene acoplada una masa puntual de valor 2m y un resorte k de rigidez 1000 N/m con el otro extremo anclado en el suelo. En la mitad del brazo izquierdo está acoplado un amortiguador viscoso de coeficiente de amortiguamiento c=100N⋅s. En el extremo derecho está acoplada una masa puntual m y una varilla de masa despreciable, rígida, acoplada a una boya de masa m, área 0,1 m2, flotando verticalmente en un estanque de agua (ρ=1000 kg/m3). La posición de la figura se corresponde con el equilibrio estático del sistema. Determinar: (a) Rigidez equivalente, momento de inercia equivalente y coeficiente de amortiguamiento relativo para el estudio de las vibraciones torsionales de la varilla. (b) Frecuencia natural y respuesta del sistema si se desplaza del equilibrio un ángulo ϕo en ausencia de excitaciones exteriores. (c) En la masa puntual de la derecha se aplica una fuerza armónica de amplitud F0=1000 N y frecuencia 1 Hz. Determinar de la respuesta permanente amplitud de la vibración y desfase.