Curso 03/04 (Segundo Parcial)
Anuncio
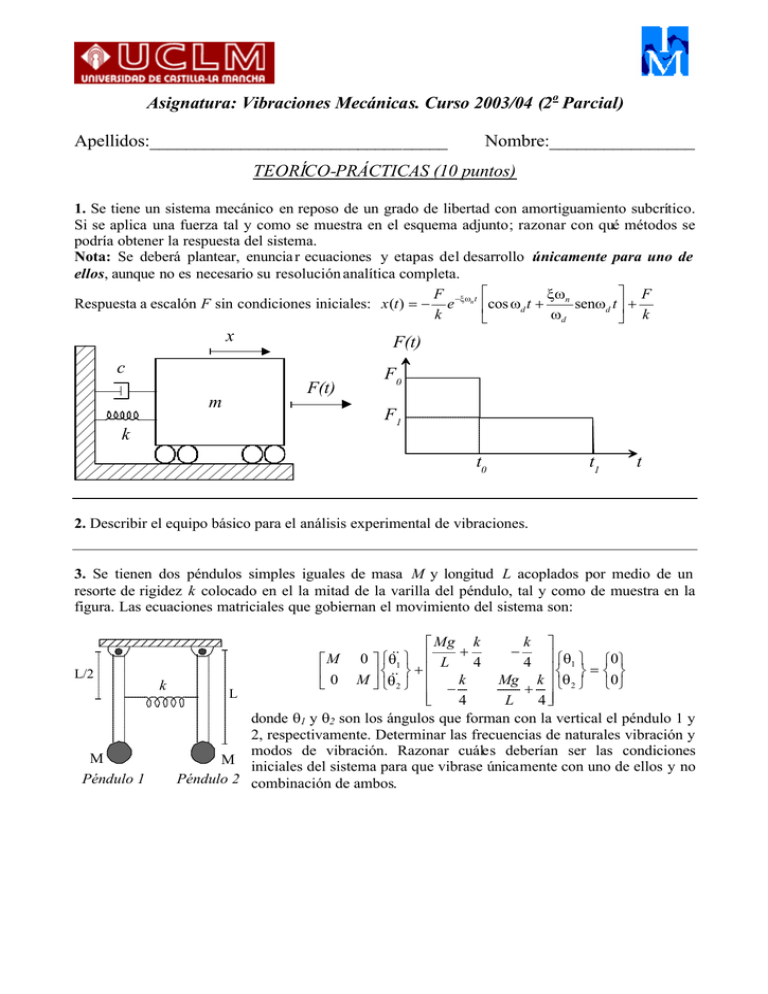
Asignatura: Vibraciones Mecánicas. Curso 2003/04 (2o Parcial) Apellidos:_________________________________ Nombre:________________ TEORÍCO-PRÁCTICAS (10 puntos) 1. Se tiene un sistema mecánico en reposo de un grado de libertad con amortiguamiento subcrítico. Si se aplica una fuerza tal y como se muestra en el esquema adjunto; razonar con qué métodos se podría obtener la respuesta del sistema. Nota: Se deberá plantear, enuncia r ecuaciones y etapas del desarrollo únicamente para uno de ellos, aunque no es necesario su resolución analítica completa. F F ξω Respuesta a escalón F sin condiciones iniciales: x (t ) = − e −ξωn t cos ωd t + n senωd t + k ωd k x F(t) c m F(t) F0 F1 k t0 t1 t 2. Describir el equipo básico para el análisis experimental de vibraciones. 3. Se tienen dos péndulos simples iguales de masa M y longitud L acoplados por medio de un resorte de rigidez k colocado en el la mitad de la varilla del péndulo, tal y como de muestra en la figura. Las ecuaciones matriciales que gobiernan el movimiento del sistema son: k Mg k − 0 θ&&1 L + 4 4 θ1 = 0 && + L/2 M θ 2 k Mg k θ 2 0 k − + L 4 L 4 donde θ1 y θ2 son los ángulos que forman con la vertical el péndulo 1 y 2, respectivamente. Determinar las frecuencias de naturales vibración y modos de vibración. Razonar cuáles deberían ser las condiciones M M iniciales del sistema para que vibrase únicamente con uno de ellos y no Péndulo 1 Péndulo 2 combinación de ambos. M 0 4. Se tiene un sistema mecánico compuesto por una varilla de masa m, una masa puntual M en el extremo de la varilla unida con resorte de rigidez 2k al suelo y del L centro de masas de la varilla cuelga una masa M/2 con un resorte M A de rigidez k, según se muestra en la figura. La varilla es rígida y x2 está articulada por su extremo A, tiene una masa m (no k 2k despreciable frente a M) y longitud L. Determinar por medio de las ecuaciones de Lagrange las matrices de masa y rigidez para el x1 estudio de las vibraciones verticales de las masas M y M/2. Datos: IG=mL2 /12 (varilla). M/2 Nota: La posición dibujada se corresponde con el equilibrio estático. PROBLEMA nº1 (5 puntos) El esquema de la figura representa una instalación de bombeo de pulpa de una planta industrial. Está constituido por un volante de inercia, un motor y un equipo de bombeo. Determinar a partir de las características técnicas del los equipos para las vibraciones torsionales: (a) las ecuaciones matriciales del sistema (b) frecuencias naturales y (c) modos propios de vibración. Razonar los resultados obtenidos. Datos para calcular rigidez de eje: Gacero =80 GPa, Keje=JejeGacero /L y Jeje=πD4 /32 Datos técnicos: Ivolante=10000 kg·m2 ; Imotor=1000 kg·m2 , Ibomba =3000 kg·m2 Eje 1: Díametro=D1 =10 cm y Longitud=L1 =2 m Eje 2: Díametro=D2 =10 cm y Longitud=L2 =1 m Volante de Inercia Eje 1 Eje 2 Motor Bomba PROBLEMA nº2 (5 puntos) En una instalación industrial se tiene una máquina compuesta por un motor eléctrico, reductor y compresor. Se observa que la máquina tiene una nivel anormalmente alto de vibraciones con una pérdida de rendimiento. Para detectar la causa del problema se efectúa un análisis en frecuencia midiendo la vibración sobre el reductor en dirección vertical. En func ión de los datos constructivos, razonar justificadamente cuáles son los defectos que sufre la máquina. Datos del motor: Potencia: 10kW Velocidad en medición: 1800 rpm Número de pares de polos: 1 Rodamientos tipo 1 Datos del compresor: Número de álabes: 12 Rodamientos tipo 1 Características técnicas Datos del reductor: Eje de entrada con rueda 16 dientes Eje intermedio con 24 dientes (entrada) Eje intermedio con 30 dientes (salida) Eje de salida con rueda 45 dientes Rodamientos tipo 1 Rodamientos de la máquina (Tipo 1): Diámetro de bolas: 8 mm Número de bolas: 12 Diámetro pista interior: 28 mm Diámetro pista exterior: 36 mm Angulo de contacto: 0º 2.5 Vibración (mm/s) 2.0 1.5 1.0 0.5 0.0 0 25 50 75 100 125 Frecuencia (Hz) 150 175 200 Solución Problema nº2 2.5 Vibración (mm/s) 2.0 1.5 1.0 0.5 0.0 0 25 50 75 100 Frecuencia (Hz) 125 150 175 200