Hoja del cap tulo 11
Anuncio

Universidad Rey Juan Carlos
Curso 2010–2011
Teorı́a de Autómatas y Lenguajes Formales
Ingenierı́a Técnica en Informática de Sistemas
Hoja de Problemas 11
Autómatas a pila
Nivel del ejercicio : () básico, (♣) medio, (♠) avanzado.
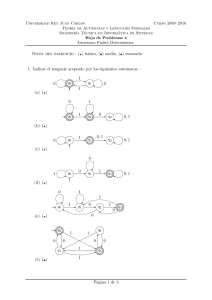
1. Para cada uno de los lenguajes siguientes, describe un autómata a pila que acepte el
lenguaje.
(a) () L = {an b2n | n ≥ 0}.
(b) () L = {xcx−1 | x ∈ {a, b}+ }.
(c) () L = {an bm | n ≤ m ≤ 3n}.
(d) (♣) L = {xcy | x, y ∈ {a, b}∗ , no subcadenas “ab” en x = no subcadenas “ba” en y}.
(e) (♣) L = {xcy | x, y ∈ {a, b}+ , no subcadenas “ab” en x = no subcadenas “ba” en y}.
(f) () L = {an bm cn+m | n, m ≥ 0}.
(g) () L = {an bm ct am+t bn | m, n > 0 , t ≥ 0}.
(h) (♣) L = {x ∈ {a, b}∗ | na (x) = nb (x)}.
(i) (♣) L = {x ∈ {a, b}∗ | na (x) = nb (x) + 1}.
(j) (♠) L = {x ∈ {a, b}∗ | na (x) = 2nb (x)}.
(k) (♣) L = amax{0,n−m} bn am | n, m ≥ 0
(l) (♣) L = {an+m bm+t at bn | n, t > 0, m ≥ 0}
2. Obtén autómatas a pila que acepten los lenguajes generados por las gramáticas siguientes :
(a) ()
S
A
B
C
::=
::=
::=
::=
aA
aABC | bB | a
b
c
Nota: Comprueba que la palabra aaabc está en el lenguaje generado por el
autómata.
(b) (♣)
A
B
C
D
::=
::=
::=
::=
2BC | 1B | λ
1D | 1C | 1
2
2D | 2C
Página 1 de 3
Hoja de Problemas 11 (cont.)
(c) (♣)
S ::= aAb | aBbb | ab | abb | λ
A ::= aAb | ab
B ::= aBbb | abb
(d) (♣)
S ::= AB | BA | 0A1 | 1A0 | 0
A ::= 0A1 | 1A0 | 0
B ::= 0B1 | 1B0 | 01 | 10
(e) (♣)
S ::= aABB | aAA
A ::= aBB | a
B ::= bBB | A
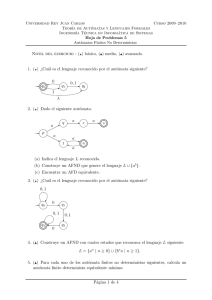
3. Obtén gramáticas que generen el lenguaje aceptado por los autómatas a pila siguientes :
(a) () AP1 = ({a, b}, {A, B}, {p, q}, A, p, f, ∅)
f (p, a, A)
f (p, a, B)
f (p, b, B)
f (q, b, B)
f (q, λ, B)
f (q, λ, A)
=
=
=
=
=
=
{(p, BA)}
{(p, BB)}
{(q, λ)}
{(q, λ)}
{(q, λ)}
{(q, λ)}
La gramática de este apartado definela en Forma Normal de Greibach.
(b) (♣) AP2 = ({a, b}, {A, z}, {q0 , q1 }, z, q0 , f, {q1 })
f (q0 , a, z) = {(q0 , Az)}
f (q0 , b, A) = {(q0 , AA)}
f (q0 , a, A) = {(q1 , λ)}
(c) (♣) AP3 = ({0, 1}, {A, B}, {p, q}, A, p, f, ∅)
f (p, 1, A)
f (p, 1, B)
f (p, 0, B)
f (q, 0, B)
f (q, λ, A)
=
=
=
=
=
Página 2 de 3
{(p, BA)}
{(p, BB)}
{(q, λ)}
{(p, λ)}
{(q, λ)}
Hoja de Problemas 11 (cont.)
(d) (♣) AP4 = ({0, 1}, {A, S}, {p, q}, S, p, f, ∅)
f (p, 0, S)
f (p, 0, A)
f (p, 1, A)
f (q, 1, A)
f (q, λ, A)
f (q, λ, S)
=
=
=
=
=
=
Página 3 de 3
{(p, AS)}
{(p, AA)}
{(q, λ)}
{(q, λ)}
{(q, λ)}
{(q, λ)}