Hoja del cap tulo 7

Universidad Rey Juan Carlos
Curso 2009–2010
Teorı́a de Autómatas y Lenguajes Formales
Ingenierı́a Técnica en Informática de Sistemas
Hoja de Problemas 6
Expresiones Regulares
Nivel del ejercicio : (⋆) básico, (♣) medio, (♠) avanzado.
1. Obtén expresiones regulares para los siguientes lenguajes:
(a) (⋆) L1 = {a2n b2m+1 | n ≥ 0 , m ≥ 0}
(b) (⋆) L2 = {w ∈ {0, 1}∗ | w tiene al menos dos ceros consecutivos}
(c) (♣) L3 = {w ∈ {0, 1}∗ | n0 (w) mod 2 6= 0}
(d) (⋆) L4 = {w ∈ {a, b}∗ | na (w) + nb (w) es par}
(e) (⋆) L5 = {an bm | n ≥ 4 , m ≤ 3}
(f) (♣) L6 = {abn w | n ≥ 3 , w ∈ {a, b}+ }
(g) (♠) L7 = {w ∈ {a, b}∗ | |w| mod 3 = 0}
(h) (♠) L8 = {w ∈ {a, b}∗ | na (w) mod 5 6= 0}
2. Obtén una expresión regular para los siguientes lenguajes sobre Σ = {a, b, c}:
(a) (⋆) Todas las cadenas que contengan una única a.
(b) (♣) Todas las cadenas que no contengan más de tres a’s.
(c) (♣) Todas las cadenas que contengan al menos una ocurrencia de cada sı́mbolo
de Σ.
(d) (♠) Todas las cadenas que no terminan en abab.
3. (⋆) Obtén, usando el método de las ecuaciones caracterı́sticas, la expresión regular
del lenguaje reconocido por el autómata siguiente:
q
a
p
a
a
r
a
s
a
u
t
a
4. (♣) Obtén, utilizando el método de las ecuaciones caracterı́sticas, la expresión regular
del lenguaje reconocido por el autómata siguiente:
Página 1 de 4
Hoja de Problemas 6 (cont.)
0, 1
q0
0
q1
0, 1
q3
0, 1
q2
0
5. Para cada uno de los autómatas finitos no deterministas siguientes, calcula su expresión regular equivalente:
1
0, λ
0, 1
q0
q1
q2
1
0
(a) (♠)
0
1
0, 1
q0
0, 1
q1
q2
1
0
(b) (♣)
λ, 0
q0
0, 1
q1
0
(c) (⋆)
q2
1
1
0, 1
q0
1
0
q3
1
0
q1
0, 1
q2
(d) (♣)
Página 2 de 4
Hoja de Problemas 6 (cont.)
1
q0
q1
1
0, 1
0
1, λ
q2
λ
q3
(e) (♣)
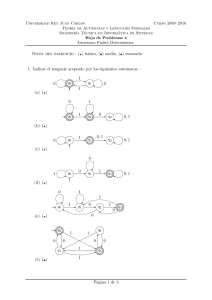
6. Indicar el lenguaje aceptado por los siguientes autómatas:
1
q0
0
q1
0
1
(a) (⋆)
0
1
q0
1
q1
0
q0
1
q1
q2
0, 1
q2
0, 1
q2
0, 1
(b) (♣)
0
0, 1
(c) (⋆)
0
q0
1
0
1
q1
(d) (♣)
0
1
1
1
q0
q1
0
q0
0
q2
1
0
q1
(f) (♠)
1
0
1
q3
0
0
(e) (♣)
1
q2
0
q3
1
Página 3 de 4
Hoja de Problemas 6 (cont.)
0
q0
0
q1
1
q2
1
1
0
q3
0, 1
(g) (⋆)
7. Obtén una expresión regular para el siguiente lenguaje:
L = {w ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}+ | wmod3 = 0}
8. Obtén un AFD mı́nimo que acepte las siguientes expresiones regulares:
(a) (⋆) ab∗ c
(b) (♣) a(bc)∗ bc
(c) (♣) a∗ b(c∗ a)∗
(d) (♣) cb∗ + aa∗
(e) (♣) b(a + b)∗ + cb∗
(f) (♠) a + ac(a + b)∗ + c(a + b + c)∗
Página 4 de 4