Hoja del cap tulo 5
Anuncio
Universidad Rey Juan Carlos
Curso 2009–2010
Teorı́a de Autómatas y Lenguajes Formales
Ingenierı́a Técnica en Informática de Sistemas
Hoja de Problemas 4
Autámatas Finitos Deterministas
Nivel del ejercicio : (⋆) básico, (♣) medio, (♠) avanzado.
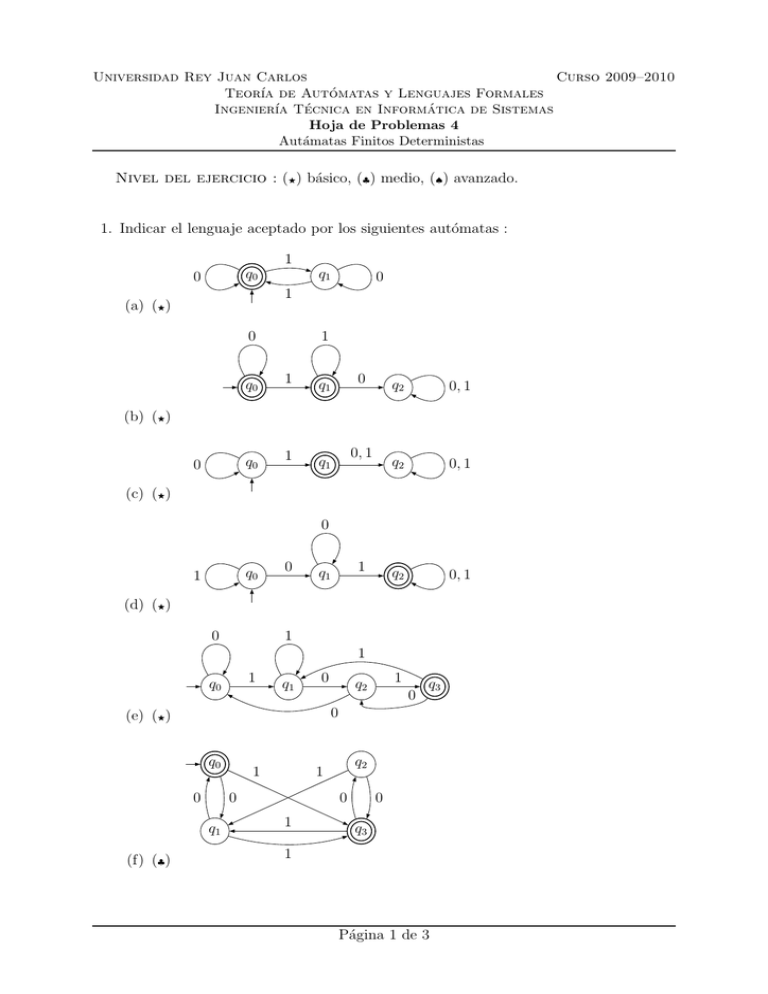
1. Indicar el lenguaje aceptado por los siguientes autómatas :
1
q0
0
q1
0
1
(a) (⋆)
0
1
q0
1
q1
q0
1
q1
0
q2
0, 1
q2
0, 1
q2
0, 1
(b) (⋆)
0
0, 1
(c) (⋆)
0
q0
1
0
1
q1
(d) (⋆)
0
1
1
1
q0
q1
0
0
q3
0
(e) (⋆)
q0
0
1
q2
1
0
q1
(f) (♣)
1
q2
0
1
0
q3
1
Página 1 de 3
Hoja de Problemas 4 (cont.)
0
q0
0
q1
1
q2
1
1
0
q3
0, 1
(g) (⋆)
2. Dado el alfabeto Σ = {a, b}, construye un autómata para cada uno de los siguientes
lenguajes :
(a) (⋆) Las cadenas que terminan en “bbb”.
(b) (⋆) Las cadenas que no contengan la secuencia “abab”.
(c) (♣) Las cadenas tal que cada bloque de cinco sı́mbolos consecutivos contienen
al menos dos b’s.
(d) (⋆) Las cadenas con un número de a’s múltiplo de tres.
(e) (♣) Las cadenas con un número par de a’s y un número de b’s múltiplo de tres.
(f) (♠) L(m, n) := {w ∈ Σ∗ | na (w) mod m = 0 y nb (w) mod n = 0}.
3. (⋆) Comprobar si los siguientes AFD son equivalentes :
AFD1 =
({a, b, c}, {p, q, r, s, t, u, v}, f1, p, {s, t, u, v})
f1 a b c
→p r t q
q q v p
r p u r
*s q t u
*t t v u
*u t t v
*v u u t
AFD2 =
({a, b, c}, {p, q, r, s, t}, f2, p, {r, s, t})
f1 a
→p s
q t
*r q
*s s
*t t
b c
q p
p q
t s
t s
s s
4. (⋆) Comprobar cuáles de los siguientes AFD son equivalentes entre sı́.
Página 2 de 3
Hoja de Problemas 4 (cont.)
AFD1 =
({a, b}, {p, q, r, s, t, u}, f1, p, {q, r})
f1 a b
→p q p
*q r s
*r q t
s t u
t s u
u q u
AFD3 =
({a, b}, {p, q, r, s, t, u}, f3, p, {s, t, u})
f3 a b
→p u q
q t r
r s r
*s t r
*t u q
*u s p
AFD5 =
({a, b}, {p, q, r, s, t}, f5, p, {r, s})
f5 a b
→p q r
q q t
*r s q
*s r q
t r q
AFD2=
({a, b}, {p, q, r, s, t, u}, f2, p, {u})
f2 a b
→p q u
q r t
r s t
s r t
t u s
*u u q
AFD4 =
({a, b}, {p, q, r, s, t, u}, f4, p, {r, s})
f4 a b
→p r q
q r q
*r s t
*s r t
t t q
u u p
AFD6 =
({a, b}, {p, q, r, s, t, u}, f6, p, {r, s, t})
f4 a b
→p q r
q p s
*r t u
*s t u
*t t u
u u u
5. (♠) Sea Σ = {0, 1} un alfabeto y sea L el lenguaje de las cadenas que consideradas
como números binarios tienen un valor entero múltiplo de 5. Demuestra que L es
regular.
Página 3 de 3