T8-Pagina_169
Anuncio

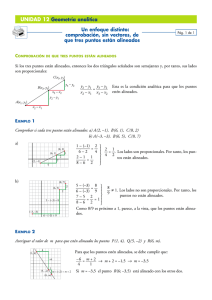
8 Soluciones a las actividades de cada epígrafe PÁGINA 169 Pág. 1 1 Comprueba si R (2, 7), S (5, –1) y T (15, –25) están alineados. Ä8 Ä8 Ä8 ° 3 RS = (5 – 2, –1 – 7) = (3, –8) 8 Ä8 ¢ 10 ? 24 8 RS no es paralelo a RT. ST = (15 – 5, –25 + 1) = (10, –24) £ Los tres puntos, R, S y T, no están alineados. 2 Averigua el valor de a para que los puntos R (2, 7), S (5, –1) y Q (a, –25) estén alineados. Ä8 ° RS = (3, –8) Ä8 ¢ Para que R, S y Q estén alineados, se ha de cumplir que: SQ = (a – 5, –24) £ 3 = –8 8 3 = 1 8 a – 5 = 9 8 Luego, a = 14. a – 5 –24 a–5 3 3 Dados los puntos A(0, 1), B(2, 5), P (x, y), averigua qué relación deben cumplir x e y para que P esté alineado con A y B. Ä8 AB = (2 – 0, 5 – 1) = (2, 4) ° 2 4 Ä8 ¢ Para que P esté alineado con A y B 8 x = y – 1 8 AP = (x – 0, y – 1) = (x, y – 1) £ 8 2 (y – 1) = 4x 8 y – 1 = 2x 8 y = 2x + 1 La relación buscada entre x e y es y = 2x + 1. 4 Averigua el valor de t para que A(1, 2), B (7, –11) y C (t, 2t) estén alineados. Ä8 AB = (7 – 1, –11 – 2) = (6, –13) ° 6 –13 Ä8 ¢ A, B y C estarán alineados si t – 1 = 2t – 2 8 AC = (t – 1, 2t – 2) £ 8 6 (2t – 2) = –13(t – 1) 8 12t – 12 = –13t + 13 8 25t = 25 8 t = 1 5 En la figura de la derecha, ¿cómo es posible que el rectángulo, que tiene 5 Ò 13 = 65 cuadritos, se pueda descomponer en los mismos cuatro fragmentos que el cuadrado, que tiene 8 Ò 8 = 64 cuadritos? El secreto está en que los puntos O, A, B y C no están alineados. C II I Compruébalo tomando O (0, 0), I II A(5, 2), B (8, 3), C (13, 5) y proB 8 II A II bando que el vector OA no es paI I 8 O ralelo al vector AB . 8 8 8 OA(5, 2) y AB = (8 – 5, 3 – 2) = (3, 1); OC(13, 5) 8 8 OA y AB no son paralelos, pues 3 ? 1 . 5 2 8 8 OC y AB no son paralelos, pues 3 ? 1 . 13 5 Los puntos O, A, B y C no están alineados. Unidad 8. Geometría analítica