(1) Respuesta: Sea t = Arctan / x ⇒ x = tan 2 t ⇒ dx = 2 tantsec 2 t dt
Anuncio

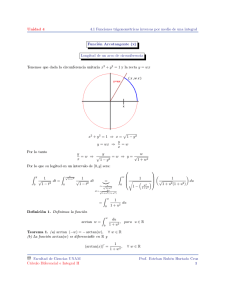
Encontrar la integral: ∫ 𝐼 := √ Arctan 𝑥 𝑑𝑥 (1) Respuesta: √ Sea 𝑡 = Arctan 𝑥 ⇒ 𝑥 = tan2 𝑡 ⇒ 𝑑𝑥 = 2 tan 𝑡 sec2 𝑡 𝑑𝑡. Si reemplazamos en (1) lo obtenido anteriormente se sigue que: ∫ 𝐼 = 2 𝑡 tan 𝑡 sec2 𝑡 𝑑𝑡 Sea 𝐽 := ∫ 𝑡 tan 𝑡 sec2 𝑡 𝑑𝑡, por lo tanto 𝐼 = 2𝐽. Definamos también: 𝑢 := 𝑡 tan 𝑡 ⇒ 𝑑𝑢 = (tan 𝑡 + 𝑡 sec2 𝑡) 𝑑𝑡 𝑑𝑣 := sec2 𝑡 𝑑𝑡 ⇒ 𝑣 = tan 𝑡 ∫ Notamos que 𝐽 = obtenemos: 𝑢 𝑑𝑣, entonces si usamos la integración por partes 𝐽 = 𝑢𝑣 − 𝐽 2 ∫ ] tan 𝑡(tan 𝑡 + 𝑡 sec2 𝑡) 𝑑𝑡 ∫ ∫ 2 2 = 𝑡 tan 𝑡 − tan 𝑡 𝑑𝑡 − 𝑡 sec2 𝑡 tan 𝑡 𝑑𝑡 ∫ 2 = 𝑡 tan 𝑡 − tan2 𝑡 𝑑𝑡 − 𝐽 = 𝑡 tan 𝑡 − ∫ 𝑣 𝑑𝑢 [ (2) De (2) se sigue que: 𝐼 = 2𝐽 = 𝑡 tan2 𝑡 − Si definimos 𝑄 := ∫ tan2 𝑡 𝑑𝑡 (3) tan2 𝑡 𝑑𝑡 y usamos la identidad tan2 𝑡 = −1 + sec2 𝑡 podemos ver que: ∫ 𝑄 = (−1 + sec2 𝑡) 𝑑𝑡 = −𝑡 + tan 𝑡 + 𝑐0 , 𝑐0 ∈ ℝ ∫ Reemplazando el valor obtenido de 𝑄 en (3), y definiendo 𝑐 := −𝑐0 ∈ ℝ se tiene que: 𝐼 = 𝑡 tan2 𝑡 + 𝑡 − tan 𝑡 + 𝑐, 𝑐∈ℝ (4) Volviendo a la 𝑥 en lo obtenido en (4) se concluye que la integral buscada es: √ √ √ 𝐼 = 𝑥Arctan 𝑥 + Arctan 𝑥 − 𝑥 + 𝑐, 𝑐∈ℝ Q.E.F.