Teorema de Bayes, variable aleatoria discreta, binomial, función de

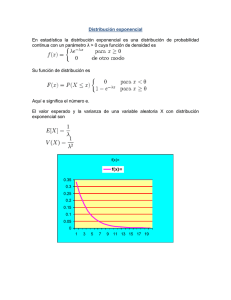
Teorema de Bayes, variable aleatoria discreta, binomial, función de probabilidad y acumulada
1) Sea X una variable aleatoria binomial, con parámetros n=8 y p=0,4. Graficar las funciones de
probabilidad y de probabilidad acumulada.
2) A partir de la siguiente gráfica adjunta de la función de probabilidad acumulada de una variable
aleatoria discreta X, hallar el recorrido de X y las siguientes probabilidades
P ( X  3)
P( X  0)
P ( X  2)
P( X  0)
P ( X  3)
P( X  4)
P ( X  3)
P( X  4)
P (2  X  4)
P( 2  X  4)
P (2  X  4)
P(0  X  7 / X  3)
P (2  X  4)
3) Se arrojan dos dados comunes. Definimos la variable aleatoria X, como la diferencia en valor
absoluto de lo que sale en las caras superiores de los dados. Hallar las funciones de probabilidad y de
probabilidad acumulada , f x ( x) y Fx ( x) respectivamente , graficarlas y hallar las probabilidades
P(3  X  4) y P(X  4/X>2) .
4) Una planta armadora recibe microcircuitos provenientes de 3 distintos fabricantes B1 , B2 y B3 ,
a B1 se le compra el doble que a B2 y a éste lo mismo que a B3 , además el porcentaje de artícu- los
defectuosos que producen es de 5, 10 y 12 % respectivamente. Si los artículos se almacenan en la
planta sin importar quién fue el proveedor:
a) Hallar la probabilidad de que una unidad armada en la planta contenga un circuito defectuoso.
b) Si un circuito no está defectuoso, ¿ cuál es la probabilidad de que provenga de B2 ?
5) Con base en varios estudios una compañía ha clasificado ha clasificado las formaciones geoLógicas en 3 tipos, I , II y III. Ella pretende perforar un pozo en determinado sitio, al que se le
asignan probabilidades de 0,35 ; 0,40 y 0,25 de pertenecer a cada tipo respectivamente. Además se
sabe que el petróleo se encuentra en un 40% de formaciones de tipo I, en un 20% de formaciones de
tipo II y en un 30% en las de tipo III. Si la compañía no descubre petróleo en ese lugar, determine la
probabilidad de que exista una formación del tipo II.
6) Un club nacional de automovilistas comienza una campaña telefónica con el propósito de aumentar
el número de miembros. Con base en experiencia previa se sabe que una de cada 20 personas que
reciben la llamada se une al club. Si en un día 25 personas reciben la llamada, ¿cuál es la probabilidad
de que por lo menos dos de ellas se asocien al club?
7) Supóngase que la probabilidad de tener una unidad defectuosa en una línea de ensamble es de 0,05.
Si el número de unidades terminadas constituye un conjunto de ensayos independientes, ¿cuál es la
probabilidad de que entre 20 unidades: a) dos se encuentren defectuosas ; b) a lo sumo dos se
encuentren defectuosas ; c) por lo menos una se encuentre defectuosa?
8) El gerente de un restaurante que sólo da servicios mediante reservación sabe, que estadísticamente,
el 15% de las personas que reservan una mesa no asistirán. Si el restaurante acepta 25 reservaciones
pero sólo dispone de 20 mesas, ¿ cuál es la probabilidad de que a todas las personas que asistan al
restaurante se les asigne una mesa?