FORMULAS FINANCIERAS
Anuncio

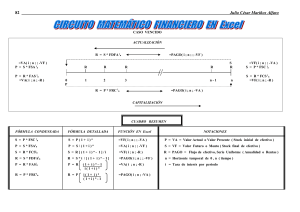
1 FORMULAS FINANCIERAS Inflación: Consiste en un aumento constante y persistente, a través del tiempo, del nivel general de precios, el cual produce una disminución del poder adquisitivo del dinero. ¿Es lo mismo recibir $1.000.000 dentro de un año que recibirlos hoy? Este fenómeno económico hace que el dinero día a día pierda poder adquisitivo, es decir, que el dinero se desvalorice. Dentro de un año se recibirá el mismo $1.000.000 pero con un menor poder de compra de bienes y servicios. El costo de oportunidad: es aquello que sacrificamos cuando tomamos una decisión. Si una persona tiene su dinero depositado en una cuenta de ahorros que le pagan el 1% mensual y le proponen un negocio; cuando decide retirarlo para invertirlo en el negocio que le han propuesto, está incurriendo en un costo de oportunidad al desprenderse del rendimiento que está obteniendo, con la esperanza de recibir mayores beneficios en el futuro, o por lo menos iguales, a lo que ya recibía. Se dice entonces, que el costo de oportunidad para esta persona es del 1% mensual. Una cantidad de dinero en el presente vale más que la misma cantidad en el futuro El interés: Es un arriendo pagado por un dinero tomado en préstamo durante un tiempo determinado. Si se presta una cantidad de dinero (P) y después de un tiempo determinado se recibe una cantidad mayor (F), la variación del valor del dinero de P a F se llama valor del dinero en el tiempo y la diferencia entre F y P es el interés (I). La operación se representa mediante la siguiente expresión: I=F–P Si se depositan en una cuenta de ahorros $500.000 y después de 6 meses se tiene un saldo de $580.000 calcular el valor del interés. I = $580.000 – $500.000 I = $80.000 Tasa de Interes: La tasa de interés (i) es la relación entre lo que se recibe de interés (I) y la cantidad prestada o invertida(P). i=I/P INTERÉS COMPUESTO: (Llamado también interés sobre interés). Es aquel que al final del periodo capitaliza los intereses causados en el periodo inmediatamente anterior. En el interés compuesto el capital cambia al final de cada periodo, debido a que los intereses se adicionan al capital para formar un nuevo capital sobre el cual se calculan los intereses. Capitalización: proceso mediante el cual los intereses que se van causando periódicamente se suman al capital anterior. VALOR FUTURO A INTERÉS COMPUESTO Consiste en calcular el valor equivalente de una cantidad P, después de estar ganando intereses por n periodos, a unas tasas de interés i. F = valor acumulado o valor futuro i = tasa de interés periódica P = valor presente de la obligación n = número de periodos El valor futuro equivalente a un valor presente está dado por la siguiente formula F = P(1 + 𝑖)𝑛 Esta fórmula es conocida como la formula básica de las Matemáticas financieras. 2 Ejercicio 1 Se invierte $1.000.000 durante 6 meses en una corporación que reconoce una tasa de interés del 3% mensual. Se desea saber ¿Cuánto dinero se tendrá acumulado al final del sexto mes? Final del primer mes: F1 = 1.000.000 + 1.000.000 x 0.03 = $1.030.000 Final del segundo mes: F1 = $1.030.000+ $1.030.000 x 0.03 = $1.060.900 Final del tercer mes: F1 = $1.060.900+ $1.060.900 x 0.03 = $1.092.727 Final del cuarto mes: F1 = $1.092.727+ $1.092.727x 0.03 = $1.125.508.81 Final del cuarto mes: F1 = $1.092.727+ $1.092.727x 0.03 = $1.125.508.81 Final del quinto mes: F1 = $1.125.508.81+ $1.125.508.810.03 = $1.159.274.07 Final del sexto mes: F1 = $1.159.274.07 + $1.159.274.07= $1.194.052.29 F = P(1 + 𝑖)𝑛 F = 1.000.000(1+0.03)^6 F = $1.194.052.29 La fórmula del interés compuesto se basa en las dos condiciones siguientes: Los intereses que se causan periodo a periodo se capitalizan, ósea que no se pagan sino que se suman al capital anterior para formar un nuevo capital. Los interés se reinvierten a la misma tasa de interés i. NOTACION TEXTO P F n I SIGNIFICADO Valor presente Valor futuro Numero de periodos Tasa de interés NOTACION EXCEL VA VF NPER TASA Ejercicio 2 Se depositan $1.000.000 durante un año, en una corporación que reconoce el 3% mensual. Calcular el valor acumulado al final del año. Con interés simple (sin reinversión de intereses) F = P(1 + ni) F = 1.000.000(1 + 12 x 0.03) F = $1.360.000 Con interés compuesto F = P (1 + 𝑖)𝑛 F = 1.000.000(1 + 0.03) ^12 F = $1.425.760.88 En Excel: = VF(tasa;nper;pago;VA;tipo) = VF(3%;12;0;-1000000) Calcular el valor acumulado después de 38 días, si se depositan $25.000.000 en una cuenta de ahorros que reconoce el 3% mensual. F = P (1 + 𝑖)𝑛 F = 25.000.000(1+0.03)^38/30 F = 25.953.772.49 3 La tasa de interés (i) y el número de periodos(n) deben estar expresados en la misma unidad de tiempo. En Excel: = VF(tasa;nper;pago;VA;tipo) = VF(3%;38/30;0;-25.000.000) Ejercicio 3 El señor Pérez entra a trabajar a una empresa ganando un sueldo mensual de $200.000 y espera recibir un aumento anual promedio del 20% ¿Cuánto quedara ganando después de 5 años? F = P (1 + 𝑖)𝑛 F = 200.000(1+0.20)^5 F = $497.664 En Excel: = VF(tasa;nper;pago;VA;tipo) = VF(20%;5;0;-200.000) En las funciones de anualidades, el efectivo que paga, por ejemplo, depósitos en cuentas de ahorros, se representa con números negativos; el efectivo que recibe, por ejemplo, cheques de dividendos, se representa con números positivos. Por ejemplo, un depósito de 1.000 $ en el banco, se representaría con el argumento -1000 si usted es el depositario y con el argumento 1000 si usted es el banco. Ejercicio 4 Dentro de 3 años Usted va a pagar $12.096.000 de un crédito que recibe hoy a una tasa de interés anual del 20% ¿Cuál es el valor del crédito? Nper VF Tasa VA 3 -12096000 20% $7.000.000,00 F = P (1 + 𝑖)𝑛 Por despeje P= F (1 + 𝑖)𝑛 P= 12096000 (1+0,2) ^3 P = 12096000 1,728 P = 7.000.000 VALOR PRESENTE A INTERES COMPUESTO Consiste en calcular el valor P, equivalente hoy a una cantidad futura F, ubicada en n periodos adelante (en el futuro), considerando una tasa de interés compuesta i. Esta operación de calcular el valor actual de un capital equivalente a lo pagado en el futuro, se presenta con mucha frecuencia en los negocios y se conoce como el procedimiento para descontar una deuda. 4 Formula: P= F (1 + 𝑖)𝑛 Ejercicio 1 El señor Pedro Picapiedra necesita disponer de $300.000 dentro de 6 meses para el pago de la matrícula de su hijo. Si una corporación le ofrece el 3.5% mensual ¿Cuánto deberá depositar hoy para lograr su objetivo? P= F (1 + 𝑖)𝑛 P= 300.000 (1+0.035)^6 P = $244.050.19