Soluciones a “Ejercicios y problemas”
Anuncio
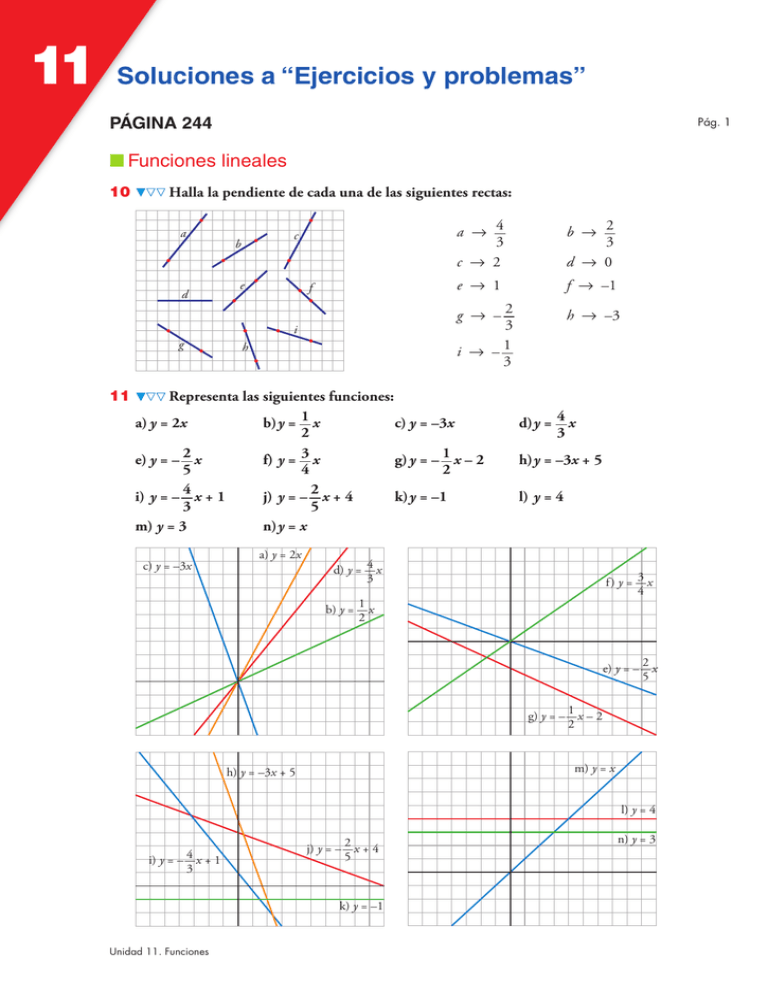
11 Soluciones a “Ejercicios y problemas” PÁGINA 244 Pág. 1 ■ Funciones lineales 10 Halla la pendiente de cada una de las siguientes rectas: a d g 11 c b e f i h a 8 4 3 c 8 2 b 8 2 3 d 8 0 e 8 1 f 8 –1 g 8 –2 3 i 8 –1 3 h 8 –3 Representa las siguientes funciones: a) y = 2x b) y = 1 x c) y = –3x 2 f) y = 3 x g) y = – 1 x – 2 e) y = – 2 x 5 4 2 j) y = – 2 x + 4 k) y = –1 i) y = – 4 x + 1 3 5 m) y = 3 n) y = x c) y = –3x a) y = 2x d) y = 4 x 3 h) y = –3x + 5 l) y = 4 4 d) y = —x 3 3 f ) y = —x 4 1 b) y = —x 2 2 e) y = –—x 5 1 –2 g) y = –—x 2 m) y = x h) y = –3x + 5 l) y = 4 4 +1 i) y = – —x 3 2 j) y = – —x +4 5 k) y = –1 Unidad 11. Funciones n) y = 3 11 Soluciones a “Ejercicios y problemas” 12 Escribe la ecuación de cada una de las siguientes funciones: c e b d f a a 8 y= 1x 2 b 8y=x c 8 y = 3x d 8 y=–3x 2 f 8 y= 2x+1 3 e 8 y=–3x+3 2 g Pág. 2 g 8 y = –2 ■ Aplica lo aprendido 13 Cada punto del diagrama siguiente representa una llamada telefónica: COSTE 2 (€) a) ¿Cuál ha sido la llamada más larga? I H b) ¿Cuál ha sido la llamada más corta? G B 0,20 D A 1 14 c) Una de las llamadas ha sido a Australia. ¿De cuál crees que se trata? C 1 5 E 10 F d) Hay varias llamadas locales. ¿Cuáles son? TIEMPO (min) a) F ha sido la llamada más larga. b) H ha sido la llamada más corta. c) H ha sido a Australia. d) A, D, E y F son locales. Representa gráficamente esta carrera de 200 m entre dos corredores: DISTANCIA (m) 200 A sale más rápidamente que B, y en 5 segundos le saca 10 m de ventaja. 180 A se cae en el instante 5 segundos, y B le adelanta. Pero A se levanta en 2 segundos, y adelanta a B en la misma línea de meta. 140 160 120 100 80 A 60 B 40 20 1 Unidad 11. Funciones (s) 9 10 TIEMPO 2 3 4 5 6 7 8 11 Soluciones a “Ejercicios y problemas” 15 Representa las siguientes funciones dando a x los valores que se indican en cada caso Enteros de –5 a 5. b) y = x 2 – 10x + 25 Enteros de 0 a 10. a) y = x 2 c) y = √x – 7 a) x y b) x y d) y = 16x – 4x 2 7, 8, 11, 16, 23, 32. –5 – 4 –3 –2 –1 25 16 9 4 1 0 0 1 1 2 4 3 9 4 5 16 25 0 1 25 16 5 0 6 1 7 4 8 9 9 10 16 25 2 9 3 4 4 1 Enteros de –3 a 7. Y a) 1 X 1 c) x y 7 0 8 1 11 16 23 32 2 3 4 5 Y c) 7 11 d) x –3 –2 –1 0 1 2 3 4 5 6 7 y –84 – 48 –20 0 12 16 12 0 –20 – 48 –84 16 X 32 23 d) Y 10 –10 2 –50 –80 16 De una familia de rectángulos cuyo perímetro es 20 cm hemos medido su base y su área. Estos son los resultados: BASE, en cm, x ÁREA, en cm2, y 1 2 3 4 5 6 7 8 9 9 16 21 24 25 24 21 16 9 a) Representa la función. b) Comprueba que la ecuación de esta función es: y = 10x – x 2 a) ÁREA 24 22 20 18 16 14 12 10 8 1 2 3 4 5 6 7 8 9 Unidad 11. Funciones BASE b) b) 10 · 1 – 12 = 9 10 · 2 – 22 = 16 10 · 3 – 32 = 21 10 · 4 – 42 = 24 10 · 5 – 52 = 25 10 · 6 – 62 = 24 10 · 7 – 72 = 21 10 · 8 – 82 = 16 10 · 9 – 92 = 9 Coincide. X Pág. 3