Ejercicio 1: En el diseño de un parque se ha previsto aprovechar
Anuncio

Matemáticas II
Curso 2007-08
INTEGRACIÓN APROXIMADA: PRUEBA DE 2º B
Ejercicio 1:
En el diseño de un parque se ha previsto aprovechar una hondonada con una profundidad
media de 2m para construir un lago como el de la figura. Tomadas las medidas
perpendiculares a un eje horizontal, con un espaciamiento horizontal de 3m, se ha obtenido la
siguiente tabla:
y 0 6 7 8 10 8 7 4 6 4 5 4 2 1 0
x 0 3 6 9 12 15 18 21 24 27 30 33 36 39 42
Usando la regla de Simpson, calcular el volumen aproximado de agua necesario para
llenarlo.
(0,3 puntos)
Solución:
El volumen del lago es aproximadamente igual al área aproximada de la sección por la
profundidad media.
El área aproximada de la sección, usando la regla de Simpson y teniendo en cuenta que las
medidas se han tomado con un espaciamiento horizontal de 3 m.,es:
3
S≈ (0+0+2(7+10+7+6+5+2)+4(6+8+8+4+4+4+1)) = 214
3
El valor aproximado del volumen es 214x2= 428 metros cúbicos.
U.D. de Matemáticas de la ETSITGC
Matemáticas II
Curso 2007-08
Ejercicio 2
Una bombilla ornamental tiene la forma de la superficie de revolución generada haciendo
1
3
1
1
girar la gráfica de y = x 2 − x 2 para 0<x< , en torno al eje x, donde x e y se miden en m.
3
3
a) Usando el método de los trapecios, estimar el área lateral de la bombilla con un error
<0,001.
b) Dar una cota del error relativo en %.
c) Usando el resultado de a), estimar la cantidad de vidrio necesario para construir la
bombilla si el espesor del vidrio es de 0,015mm.
(0,7 puntos)
Solución:
1
3
1
a) El área lateral de la figura generada por la función y = x 2 − x 2 al girar
3
alrededor del eje de abscisas en [0,1/3], es S L = ∫
1
0
#19:
#20:
S
=
3 2πy
1 + ( y ')2 dx
d 1
3/2
&'√x - x
dx 3
1
3√x
&' - &', luego
6√x
2
1/3
⌠
1
3/2
1
3√x 2
2π&'√x - x
√1 + &' - &' dx
⌡
3
6√x
2
0
Con el comando aproximar de DERIVE se obtiene SL≈0.1163552834
Para obtener una aproximación de SL aplicando el método de los trapecios, hemos de tomar la
función integrando como la función f(x) de dicha fórmula:
#25:
1
3/2
1
3√x 2
f(x) ≔ 2π&'√x - x
√1 + &' - &'
3
6√x
2
Una cota del error cometido viene dado por la expresión:
h2
(b − a ) M donde M = máx{ f ' ' ( x ) , a < x < b}.
12
Calculamos, en primer lugar, el máximo M o una cota de f’’(x) en [0,1/3]
#26:
d 2 1
3/2
1
3√x 2
2π&'√x - x
√1 + &' - &'
dx 3
6√x
2
- 6π·SIGN(x·(9·x + 1))
U.D. de Matemáticas de la ETSITGC
Matemáticas II
Curso 2007-08
Pero esta función es constante pues la función signo solo puede tomar los valores 1 ó -1 por
lo que - 6π·SIGN(x·(9·x + 1))= 6π y la representación gráfica es:
If(0<x<1/3, 6π)
Luego M=6π<20, y en este caso:
2
1 3 − 0
2
h
5
n 1
(b − a ) M =
< 0,001 , despejando n, y tomando n positivo, se
− 0 20 =
12
12
3
81n 2
obtiene n>7,86, es decir el primer número natural n que verifica la desigualdad es n=8, luego:
1 −0
1
1
k
y los puntos de la partición son xk = 0 + k
h= 3
=
=
, luego necesitamos los
8
24
24 24
valores de la función, para k = 0, 1, 2, ···,8.
k
Definimos en Derive la función auxiliar g(k):= f
24
-27
13
g(k) := 3.195597754·10 (2.106396961·10 - 2.632996202·1012 ·k)·√(3.781748192·1024 ·k2
+ 2.016932369·10·k + 2.689243158·1025) y entonces:
7
1 / 24
SL≈
g
(
0
)
+
g
(
8
)
+
2
g (k ) ≈ 0.115 m2
∑
2
1
Observa que nos quedamos con solo 3 cifras decimales pues el error < 0.001, por lo tanto, no
podemos dar información fiable desde la cuarta cifra decimal en adelante.
(Nota: Si tomamos como función f el integrando sin el factor 2π, el error queda dividido por
2π y se obtiene n=4, pero la aproximación de la integral queda afectada.)
b) El error relativo en % es er=
0,001
100 ≈ 0,87%
0,115
c) 0,015mm= 0,000015 m, luego la cantidad de vidrio necesaria es: 0.115*0,000015 ≈
0.000001725 m3 = 1,725 cm3.
U.D. de Matemáticas de la ETSITGC
Matemáticas II
Curso 2007-08
INTEGRACIÓN APROXIMADA: PRUEBA DE 2º A
Ejercicio 1
1. Los hilos de un tendido eléctrico, suspendidos cada dos postes, adoptan la forma de una
catenaria de ecuación
x
y = 20 cosh
donde -20 ≤ x ≤ 20
20
donde x e y se miden en metros. Se pide
a) Calcular, de forma aproximada y con un error menor que 1mm, la longitud del cable
suspendido entre dos postes utilizando la regla de Simpson.
b) Dar una cota del error relativo en %
(0,6 puntos)
Solución:
a) La longitud del cable suspendido entre dos postes es:
L=∫
20
−20
1 + ( y ')2 dx = 2 ∫
20
0
1 + ( y ')2 dx
x
20
Con el comando aproximar se obtiene 47.00804774
La función f(x) que necesitamos es la función integrando:
donde y = 20 cosh
f ( x ) = 2 1 + ( y ')
2
x
−x
−x
x 20
e 20
e 20
e 20
e
= 2 1+
−
=
+
2 160000 160000
2
Una cota del error cometido viene dado por la expresión:
{
}
h4
(b − a ) M donde M = máx f ( 4 ( x ) , a < x < b .
180
Calculamos, en primer lugar, el máximo M o una cota de f(4(x), en valor absoluto, en [0,20]
#29:
#30:
x/20
- x/20 2
x/20
- x/20
d 4
e
e
e
e
2√1 + &' - &' = &' + &'
dx
2
2
160000
160000
x/20
- x/20
e
e
IF0 < x < 20, &' + &'
160000
160000
U.D. de Matemáticas de la ETSITGC
Matemáticas II
Curso 2007-08
e
e −1
+
≈ 1.928850793·10-5
160000 160000
(4
Luego una cota superior de f (x) en [0,20] es 2·10-5<0,0001 (como se observa en la gráfica)
20 4
&'
#33:
n
&'200.0001 < 0.001
180
El máximo se alcanza en x=20, es decir,
3/4
3/4
2√310
2√310
n < - &' ∨ n > &'
3
3
n < -6.493358309 ∨ n > 6.493358309
#34:
20 − 0 20
y los valores x
=
8
8
de la partición son x = 0+20k/8=20k/8 y los valores de f(x) en estos puntos son:
El valor positivo y par más pequeño es n= 8, en consecuencia, h=
20k
k/8
- k/8
f&' = e
+ e
8
#36:
Por comodidad definimos
#37:
k/8
- k/8
g(k) ≔ e
+ e
20
&'
#38:
8
3
3
&'g(0) + g(8) + 2 ∑ g(2k) + 4 ∑ g(2k + 1) = 47.0081
3
k=1
k=0
Observa que nos quedamos con solo 3 cifras decimales pues el error < 0.001, por lo tanto, no
podemos dar información fiable desde la cuarta cifra decimal en adelante.
(Nota: Si tomamos como función f(x) el integrando sin el factor 2, el error queda dividido
por 2, ahora bien como hemos tomado el intervalo [0,20], en lugar de[-20,20] quedaría
compensado.)
b) El error relativo en % es er=
0,001
100 ≈ 0.002%
47,008
U.D. de Matemáticas de la ETSITGC
Matemáticas II
Curso 2007-08
Ejercicio 2
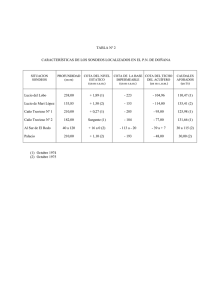
La figura muestra un terreno acotado por dos carreteras y un rio. Todas las medidas se dan en
m. y vienen dadas por la tabla siguiente:
y 540 390 390 430 425 450 360 300 275 125 0
50 100 150 200 250 300 350 400 450 500
x 0
0
500
a) Aproximar el área de la propiedad usando la regla de los trapecios.
b) Indica el procedimiento para calcular de manera aproximada la longitud del río que
acota dicha propiedad.
(0,4 puntos)
Solución:
a) El área aproximada del terreno, usando el método de los trapecios y teniendo en cuenta
que las medidas se han tomado con un espaciamiento horizontal de 50 m.(n=10
intervalos),es:
50
S≈ (0+540+2(390+390+430+425+450+360+300+275+125)) = 170150 m2.
2
b) La longitud del río es una medida líneal y, por tanto, se puede aproximar midiendo la
poligonal determinada por los puntos de la medición. Así en el primer subintervalo el
50 2 + ( y1 − y 0 )2 , en consecuencia,
segmento correspondiente de la poligonal mide
La longitud de la diagonal es:
10
∑
50 2 + ( y k − y k −1 )2 ≈ longitud del río
1
y0
y1
U.D. de Matemáticas de la ETSITGC