Clase 10

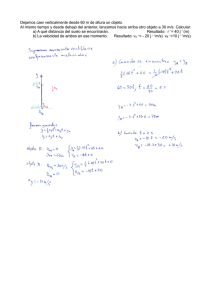
Cinemática. Repaso.
Problema 6.72
• Un auto viaja hacia el Este con una
rapidez de 50 km/h. Esta lloviendo
verticalmente con respecto a la Tierra. Las
marcas de la lluvia sobre las ventanas
laterales del automóvil forman un ángulo
de 60 grados con la vertical.
• Calcule la velocidad de la lluvia con
respecto al automóvil y con respecto a la
Tierra.
Que tenemos:
• v – velocidad de la lluvia con respecto de la Tierra.
• vlluvia - velocidad de la lluvia con respecto del auto.
• vauto= 50 km/h
• θ = 60 grados con la vertical
• v=vauto + vlluvia
Ahora nos preguntamos, ¿cuántas ecuaciones
describen este problema?
v= vx+vy
vx=vcosθ
vy= vsenθ
1. Velocidad de la lluvia con respecto del auto
Vauto=vlluvia senθ 50=vlluvia sen60 = 58 km/h
2. Velocidad de la lluvia con respecto de la Tierra: v
V = vlluvia cosθ = 58 cos60 = 29 km/h.
3.13 - Un automóvil y un camión parten
simultáneamente, desde el reposo, con el auto a
cierta distancia detrás del camión. Ambos se
mueven con aceleración constante, de 1.8 m/s2
para el automóvil y de 1.2 m/s2 para el camión, y
se cruzan cuando el auto se encuentra a 45 m de
su lugar de partida. Calcular:
a - Cuánto tiempo tardó el auto en alcanzar al
camión.
b - Qué distancia los separaba inicialmente.
c - La velocidad de cada vehículo cuando
están a la par.
Comenzamos con un esquema.
•
Ahora nos preguntamos, ¿cuántas ecuaciones describen este problema?
•
Ya que acá tenemos dos movimientos uniformemente variados, y cada
se describe con dos ecuaciones del tipo:
x = xo + vo ( t – to ) + ½ a ( t – to )2
•
•
v= vo + a ( t – to )
Para resolver de nuestro problema tenemos que reemplazar las constantes de las
ecuaciones (to , xo , vo y a) por las "iniciales" de cada movimiento.
Auto
xA = 0.9 m/s2 . t A2
vA = 1.8 m/s2 . tA
•
Camión
xC = d + 0.6 m/s2 . tC 2
vC = 1.2 m/s2 . tC
•
Encuentro: xA=xC=45m
xA= 45 = 0.9. t E2 (1)
45 = xC = d + 0.6 m/s2 . tE 2 (2)
vAE=1.8.tE
VcE=1.2.tE
•
•
(3)
tE=7.07s de (1)
VAe=12.7 m/s
D=15 m de (3)
VCe=8.48 m/s
(4)
una circunferencia entera, pegar una vuelta completa, una
revolución exacta, 360 grados.Se mide en cualquier unidad de
tiempo, para hacer cálculo tratá de elegir siempre segundos.
Frecuencia, ƒ es la cantidad de giros, o vueltas. Si la unidad de
tiempo es el segundo (la más usada), la unidad de frecuencia es
el s-1 o lo que es lo mismo, el Hz (Hertz)
Entre período y frecuencia existe una relación obvia: uno es el
inverso del otro.
T=1/ƒ
ƒ=1/T
Y para velocidad angular se usan las vueltas o revoluciones por minuto, con
unidad de medida rev/min. Siempre se debe tener en
mente que las vueltas o revoluciones son medidas de ángulo, por lo tanto
son un número adimensional.
T=1/n
Si T es periodo ω=2π/T =2πn o v = 2πr/T o v = 2πr n
Problema 6.2
6.2 - Un satélite artificial gira alrededor de la
Tierra, completando un ciclo en
aproximadamente 90 minutos. Suponiendo que
su órbita es circular, que el radio medio de la
Tierra es 6370 km, y que la altura media del
satélite sobre su superficie es 280 km, determinar
su velocidad tangencial.
Problema 6.2
RT=6370 km
h=280 km
T= 90 min
La altura a la que orbita el satétile, h, más
el radio terrestre, RT , es igual al radio
de órbita, R.
R = RT + h = 6370 km + 280 km = 6650
km
V=R.ω
ω=2π/T
V=R.2π/T
Unidades del sistema internacional: T,
el período en segundos y R, el radio,
en metros.
V = 7.737 m/s
• 3.27 - Un globo de gas asciende
verticalmente con velocidad constante de 10
m/s. Cuando se encuentra a 16 m del piso,
un muchacho que está debajo le dispara una
piedra con su gomera, la que parte
verticalmente a 30 m/s desde una altura de 1
m.
¿A qué distancia del piso alcanzará la piedra
al globo?
• ¿Cuánto tiempo después de partir?
• ¿Cuál será la velocidad de la piedra
(respecto a la tierra) en ese instante?
Problema. 3.27
•
•
3.7 - El conductor de un
tren subterráneo de 40 m
de longitud, y que
marcha a 15 m/s, debe
aplicar los frenos 50 m
antes de entrar en una
estación cuyo andén
mide 100 m de longitud.
Calcular entre qué
valores debe hallarse el
de la aceleración de
frenado, para que el tren
se detenga dentro de los
límites del andén.
Rsp. amax=1.25 m/s2
amin=0.75 m/s2
Problema 5
• Se dispara un cuerpo verticalmente hacia
arriba con velocidad de 80 m/s. Calcular
el tiempo que demora en alcanzar su
máxima altura. Supongamos que g=10
m/s.
Rps. t=8s.
• 3.7 - El conductor de un tren
subterráneo de 40 m de longitud, y que
marcha a 15 m/s, debe aplicar los
frenos 50 m antes de entrar en una
estación cuyo andén mide 100 m de
longitud.
Calcular entre qué valores debe
hallarse el de la aceleración de frenado,
para que el tren se detenga dentro de
los límites del andén.
Problema 6
•
•
•
•
•
•
Una piedra es lanzada verticalmente hacia
arriba con una velocidad de 10 m/s. (g=10
m/s). Se pide:
a). Calcular la altura que subirá.
b). El tiempo que demora en subir – Rsp. 1s.
c). El tiempo que demora en bajar – Rsp. 1s.
d). El tiempo que demora en regresar al lugar
de partida- Rsp. 2s.
e). La velocidad de llegada – Rsp.10 m/s.
Problema 7
•
•
En la boca de un pozo se deja caer un
cuerpo y una persona ubicada en el
borde de esta escucha el sonido del
impacto luego de 51 segundos. Cual es
la profundidad del pozo? ( Vsonido=340
m/s, g=10 m/s).
Rsp. 5780 m
Problema 5.13
• 5.13 - ¿Cuál es el ángulo de inclinación para el cual es
mayor el alcance de un tiro oblicuo? Puede trabajar con la
parábola de tiro usando las relaciones entre las funciones
trigonométricas. Rsp. 45 grados.
Ejercicio 6.29.
Un aeroplano que vuela horizontalmente a 1 km de altura
y con una rapidez de 200 km/h, deja caer una bomba
contra un barco que viaja en la misma dirección con
una rapidez de 20 km/h. Pruebe que la bomba debe
soltarse cuando la distancia horizontal entre el avión y
el barco es de 705m. (g=10 m/s2)
Ejemplo 3.7. Un disco de 10 cm de radio que gira a 30
rev/min demora un minuto en detenerse cuando se lo
frena. Calcular:
a) su aceleración angular,
b) el número de revoluciones hasta detenerse,
c) la rapidez tangencial de un punto del borde del disco
antes de empezar a frenar,
d) la aceleración centrípeta, tangencial y total para un
punto del borde del disco.