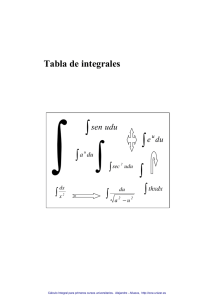
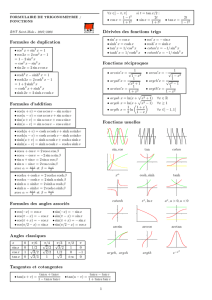
Integral Berehalakoen Taula
Anuncio

Integral Indefinida f(x) dx = F(x) + C (C ) : F'(x) = f(x) F(x): función Primitiva de f(x) Operador Lineal k f(x) dx = k f(x) dx k f(x) + g(x) +... dx f(x) dx + g(x) dx +.... k f(x) + m g(x) +... dx k f(x) dx + m g(x) dx +.... MÉTODOS de Integración Transformación de Funciones SUSTITUCIÓN Por PARTES DESCOMPOSICIÓN Integral INMEDIATA Primitivas de las funciones Inversas: Arc sen , Arc cos , Arg Sh , ...... Logaritmos. Producto de funciones distintas...... v '( x ) Modelos: u ( x ) v '( x ) dx ; u ( x ) dx k Por PARTES Ejemplos : 1) I ax P ( x ) e dx ; P ( x ) sin x dx ; P ( x ) shx dx u ( x ) = Ln x du = 2) I Ln x dx dv =dx v = dx SUSTITUCIÓN Ejemplos : 3) dv = g dx v = I uv u ( x ) = P ( x ) du = u' ( x ) dx g dx v du Funciones Irracionales x 2 dx I 3 4+ x = t I 1 3 dt 3 x dx d t t 4+x 4 dx 4 dx dt x + 3 = 5t 4) I I 2 2 2 2 dx 5d t ( x + 3) + 5 t +1 x + 6 x + 25 5) 3 3 2 3 dt chx t shx dx I 2 shx dx d t 3ch 2 x 6 3t 6 I I u v v du = ....... Tabla de Integrales INMEDIATAS dx x C x x dx n 1 C 1 x dx 2 x C sin x dx cos x C cos x dx sin x C Sh x dx Ch x C Ch x dx Sh x C n 1 ( n 1) : n x m dx x m / n dx n m 1 n x C m 1 n e dx e C 1 dx ln x C x 1 dx ln x a C xa 1 1 C dx 2 x x ax x a dx C ln a x I(x): Irracional 1 1 x2 1 x 1 1 2 x2 1 x dx x dx 1 x2 1 x x dx x 1 2 dx k u ( x) = t u' ( x ) dx d t 1 x 1 x 1 2 1 2 f(t ) dt = ....... k R(x): Racional R( x ) = Q( x) dx P( x ) 1 dx ln x C x * 1 I dx Arctgx C 1 dx ln x a C xa Bdx ( xa)-n+1 C B C n -n+1 ( x a) dx 1 x Arc tg C 2 ax a a ** dx ArgThx C ax dx 2 1 x ArgTh C a a (a>0) (a>0) dx A rc sin x C x ¹ x-a dx A rg C h x C 1 ¹ b2 dx A rg S h x C b ( x a) dx 2 1 xa Arg Th C b b 1 x2 C 1 x C 2 2 Chx dx ln Shx C Shx f ( x b) dx F ( x b) C u' 1 ¹ a (a > 0) 1 dx Thx C Ch 2 x 1 (Coth 2 x 1) dx dx Coth x C Sh 2 x Cothx dx 1 Shx dx ln(Chx) C Chx f( x) dx F( x) + C f (ax+b) dx a F(ax+b) + C (III) I f(u ) Thx dx f( x ) + C n (1 Th 2 x) dx cos x f ( x) dx = L (II) 1 (1 tg x) dx dx tg x C cos 2 x 1 (1 ctg 2 x) dx dx ctg x C sin 2 x sin x dx ln cos x C cos x ctg x dx sin x dx ln sin x C f '( x ) (I) x 2 tg x dx x2 1 C M( x - a) N ( x - a) b 2 2 dx = 2 = ( M (I) M 2 Ndx N xa Arc tg C 2 2 ( x a) b b b 2( x - a) x - a) b 2 2 Ln [( x - a) b 2 ( dx + 2 ]+ N b N x - a) b Arctg 2 x-a b 2 dx = +C