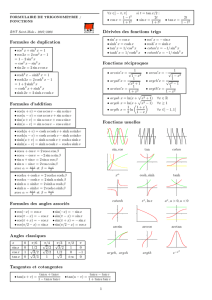
u dx uc
Anuncio

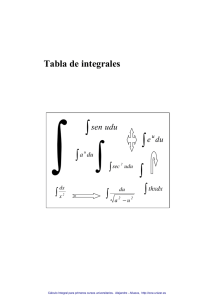
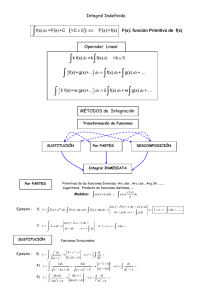
Resumen de Análisis matemático Página 12 Cuadro de integrales inmediatas dx x c u' dx u c u n 1 u' u dx n 1 c u' u dx Lu c u' e u' a n dx n u dx e u c u' sen(u)dx cos(u) c an c La u' cos(u)dx sen(u) c u'dx cos 2 u u' (1 tg 2 (u))dx tg(u) c u' dx sen arcsen( u) c 1 u2 u' dx 1 u2 arctg(u) c u' sh(u) ch(u) c u' ch(u) sh(u) c u'dx u' (1 cot g 2 ( u))dx cot g( u) c 2 u u' dx arg sh( u) c 1 u2 u' dx 1 u 2 arg th(u) c u' dx u2 1 arg ch( u) c Sustituciones recomendadas Función R( x, e x )dx R( x, Lx )dx R( x, arctg( x ))dx Cambio ex = t Lx = t arctg(x) = t Cálculos x=Lt x = et dt ; dx t ; dx = et dt dt cos 2 x = x = sen(t) ; dx = cos(t) dt R( x, arcsen( x ))dx arcsen(x) t = x = cos(t) ; dx = -sen(t) dt R( x, arccos( x ))dx arccos(x) t R( x, arg th( x ))dx argth(x) = t x = th(t) ; dx dt2 ch x R( x, arg sh( x ))dx argsh(x) = t x = sh(t) ; dx = ch(t) dt R( x, arg ch( x ))dx x = tg(t) argch(x) = t x = ch(t) ; dx ; dx = sh(t) dt Sustituciones en integrales de funciones trigonométricas circulares Si es impar en SEN X cos x = t x = arccos(t); dx dt 1 t 2 ; sen( x ) 1 t 2