De la ecuación PV nRT , tenemos que , así que PV RT = , dividiendo

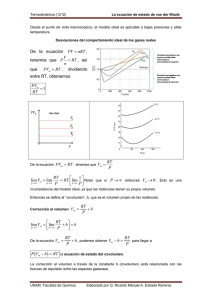
Termodinámica (1212)
La ecuación de estado de Van der Waals
Desde el punto de vista macroscópico, el modelo ideal es aplicable a bajas presiones y altas
temperatura.
Desviaciones del comportamiento ideal de los gases reales
De la ecuación
PV  nRT ,
V
 RT , así
n
PVm  RT , dividiendo
tenemos que P
que
entre RT, obtenemos
PVm
1
RT
Gas real
De la ecuación
PVm  RT , tenemos que Vm 
RT
P
RT
1

 RT  lim  Notar que si P   entonces Vm  0 . Esto es una
p  P
 p P 
lim Vm  lim
p 
inconsistencia del modelo ideal, ya que las moléculas tienen su propio volumen.
Entonces se define al “covolumen”, b, que es el volumen propio de las moléculas.
Corrección al volumen:
Vm 
RT
b
P
RT


lim Vm   lim
 b  b
p 
 p P

De la ecuación
Vm 
RT
RT
para llegar a
 b , podemos obtener Vm  b 
P
P
P Vm  b   RT la ecuación de estado del covolumen.
La corrección al volumen a través de la constante b (covolumen) está relacionada con las
fuerzas de repulsión entre las especies gaseosas.
UNAM. Facultad de Química. Elaborado por RMAER para el grupo 14
Termodinámica (1212)
La ecuación de estado de Van der Waals
Algunos arreglos posibles
Vm 
P Vm  b   RT
V
n
V

P   b   RT
n

Vm 
Multiplicando por n
RT
b
P
Multiplicando por
V

Pn   b   nRT
n

P
RT
PVm
bP
 1
RT
RT
P V  nb   nRT
Corrección por las fuerzas de atracción
Asumiendo que las moléculas son esféricas,
tenemos que
Distancia
4
Vm   r 3 elevando al cuadrado
3
Energía
Vm 2 
r6 
Fatracción  k
1
 9Vm 2 

2 
 16 
k
16 2 6
 r despejando r6
9
9Vm 2
1
recordar que Fatracción  k 6
2
r
16
16 2
dividiendo entre el área
9Vm 2
Fatracción
16 2
16 2
a
y
hacemos
que
con lo cual obtenemos Patracción 
k
a

k
2
A
9A
9 AVm
Vm 2
Recordar que ya habíamos obtenido
P Vm  b   RT , que también se puede expresar como
P
RT
a
introduciendo
obtenemos
Vm 2
Vm  b 
P
RT
a
 2 Ecuación de estado de Van der Waals para gases reales.
Vm  b  Vm
Las constantes a y b se llaman los coeficientes de Van der Waals y tienen valores
característicos para cada gas.
Bibliografía recomendada: Atkins, P.W., Fisicoquímica, 3ª ed. U.S.A., Addison-Wesley
Iberoamericana, 1991.
UNAM. Facultad de Química. Elaborado por RMAER para el grupo 14