Apuntes1
Anuncio
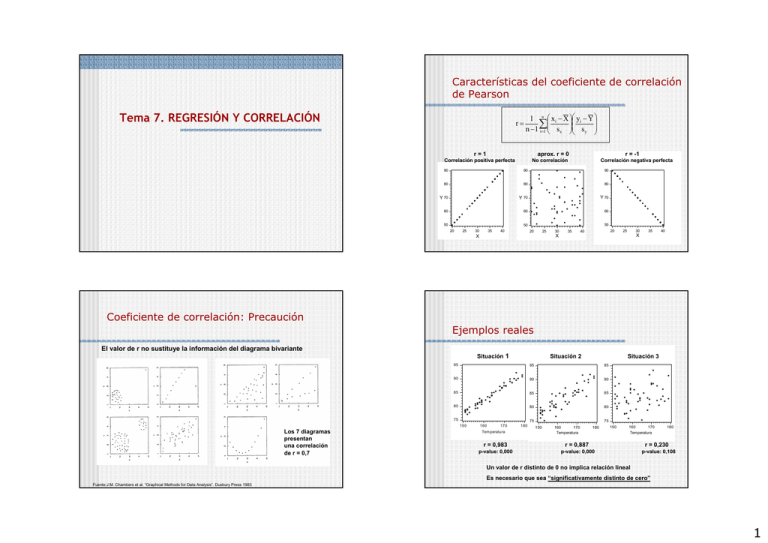
Características del coeficiente de correlación de Pearson Tema 7. REGRESIÓN Y CORRELACIÓN r= 1 n xi − X yi − Y ∑ n −1 i=1 sx s y r=1 aprox. r = 0 Correlación positiva perfecta r = -1 No correlación Correlación negativa perfecta 90 90 90 80 80 80 Y 70 Y 70 Y 70 60 60 60 50 50 50 20 25 30 35 40 20 25 X 30 X 35 20 40 25 30 X 35 40 Coeficiente de correlación: Precaución Ejemplos reales El valor de r no sustituye la información del diagrama bivariante Situación 1 Situación 2 95 95 90 90 90 85 85 85 80 80 80 75 75 75 150 Los 7 diagramas presentan una correlación de r = 0,7 Situación 3 95 160 170 Tem peratura 180 150 160 170 Temperatura 180 r = 0,983 r = 0,887 p-value: 0,000 p-value: 0,000 150 160 170 Temperatura 180 r = 0,230 p-value: 0,108 Un valor de r distinto de 0 no implica relación lineal Es necesario que sea “significativamente distinto de cero” Fuente:J.M. Chambers et al. “Graphical Methods for Data Analysis”. Duxbury Press 1983 1 Coeficiente de correlación: Interpretación del p-valor Coeficiente de correlación: Tablas para valorar la significación Valores de r que dan niveles de significación (p-valor) del 5 y del 1 % Ref. Pere Grima Situación 3 r = 0,230 95 p-value: 0,108 n p-valor 0,05 0,01 3 0,997 1 4 0,95 5 6 p-valor n p-valor n 0,05 0,01 0,05 16 0,497 0,623 0,01 29 0,367 0,471 0,99 17 0,482 0,606 30 0,361 0,463 0,878 0,959 18 0,468 0,59 35 0,334 0,43 0,811 0,917 19 0,456 0,575 40 0,312 0,403 7 0,754 0,875 20 0,444 0,561 45 0,294 0,38 8 0,707 0,834 21 0,433 0,549 50 0,279 0,361 9 0,666 0,798 22 0,423 0,537 55 0,266 0,345 10 0,632 0,765 23 0,413 0,526 60 0,254 0,33 11 0,602 0,735 24 0,404 0,515 65 0,244 0,317 12 0,576 0,708 25 0,396 0,505 70 0,235 0,306 13 0,553 0,684 26 0,388 0,496 75 0,227 0,296 14 0,532 0,661 27 0,381 0,487 80 0,22 0,286 15 0,514 0,641 28 0,374 0,479 85 0,213 0,278 90 85 80 75 Pero, ¿qué significa p-value = 0,108 ? 150 160 170 Temperatura 180 Es el resultado de realizar un test para comprobar la hipótesis de independencia entre las variables consideradas (solo si p<0,05 se rechaza la hipótesis, porque sería muy poco probable que dos variables independientes “dieran un r con ese valor”) Coeficiente de correlación: Interpretación del p-value Análisis de los residuos: 3 situaciones distintas de residuos Valores de r obtenidos al realizar 10.000 simulaciones con muestras INDEPENDIENTES El 10,8 % de los casos [(536+558) /1000] da un valor de |r| > 0,23 600 Frequency 500 400 536 casos Los residuos no contienen información. El modelo propuesto es el adecuado 558 casos 300 e Valores correspondientes a las situaciones 1 y 2 200 Los residuos contienen información. la relación entre X e Y parece no ser lineal e La recta será menos precisa para valores grandes de x, que para valores pequeños. e 100 0 0 -1,0 -0,8 -0,6 -0,4 -0,2 0,0 -0,23 0,2 0,4 y 0 y 0 y 0,6 0,8 1,0 0,23 2 Cuidado con: Observaciones “raras” Observación atípica: observación que no encaja en el aspecto general de la nube de puntos del gráfico de dispersión (puede serlo por tener un valor muy distanciado del resto en la y, en la x o en ambas) Observación influyente: aquella que si la eliminamos del estudio, produce un cambio notable en la posición de la recta de regresión (normalmente valores grandes de x. Su residuo puede ser pequeño) y Cuidado con: Extrapolación Extrapolación: utilización de la recta de regresión para predecir fuera de los valores observados y Previsión Obs. atípica Valor real Modelo correcto Obs. atípica e influyente x x Cuidado con: Variables latentes y relaciones causa-efecto La relación entre dos variables puede estar influida por otras que no sospechamos su existencia o simplemente no las medimos. A éstas se les llama variables latentes. Una fuerte asociación entre 2 variables no es suficiente para sacar conclusiones sobre relaciones causa-efecto. La mejor manera de evidenciar de que una asociación se debe a la causalidad, se obtiene mediante las ténicas DOE 3







