Dipolos perpendiculares con carga inductiva

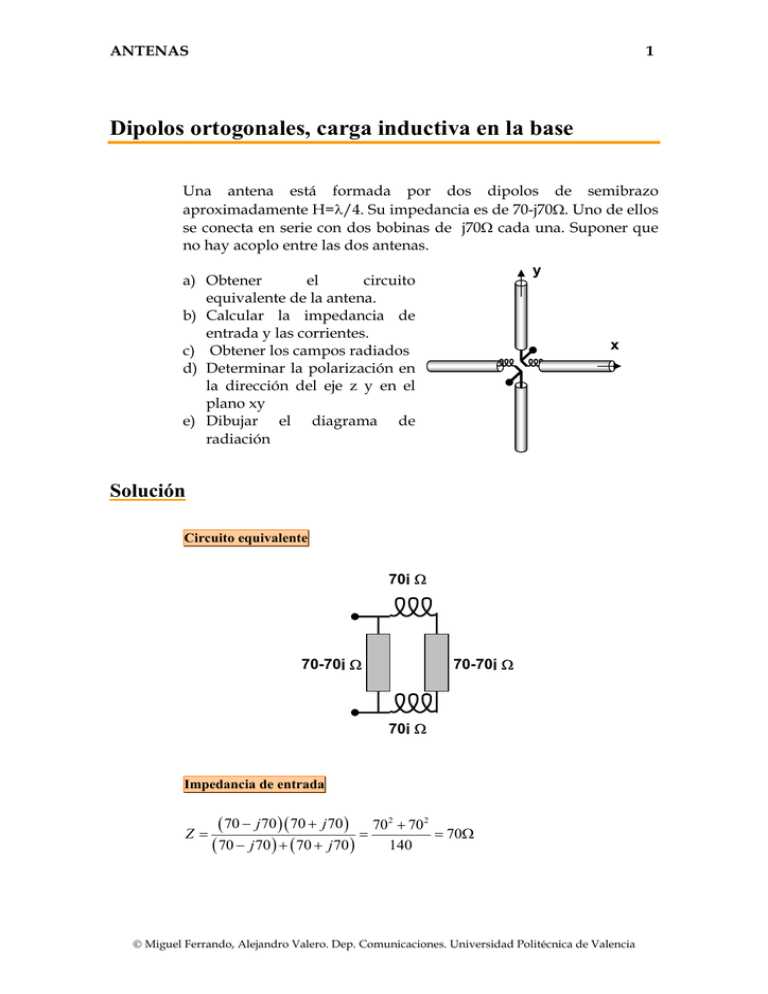
ANTENAS
1
Dipolos ortogonales, carga inductiva en la base
Una antena está formada por dos dipolos de semibrazo
aproximadamente H=λ/4. Su impedancia es de 70-j70Ω. Uno de ellos
se conecta en serie con dos bobinas de j70Ω cada una. Suponer que
no hay acoplo entre las dos antenas.
y
a) Obtener
el
circuito
equivalente de la antena.
b) Calcular la impedancia de
entrada y las corrientes.
c) Obtener los campos radiados
d) Determinar la polarización en
la dirección del eje z y en el
plano xy
e) Dibujar el diagrama de
radiación
x
Solución
Circuito equivalente
70j Ω
70-70j Ω
70-70j Ω
70j Ω
Impedancia de entrada
Z=
( 70 − j 70 )( 70 + j 70 ) = 702 + 702
140
( 70 − j 70 ) + ( 70 + j 70 )
= 70Ω
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
2
Corrientes
Corriente a la entrada
I=
V
70
Corriente en los dipolos
Iy =
V
70 + j 70
1 j π4
⎛ 1+ j ⎞
I
e
=I
=I⎜
=
⎟
70 − j 70
140
2
⎝ 2 ⎠
Ix =
V
70 − j 70
1 − j π4
⎛ 1− j ⎞
=I
=I⎜
=
I
e
⎟
70 + j 70
140
2
⎝ 2 ⎠
Se puede observar que las corrientes tienen el mismo módulo y están
desfasadas 90o.
Vector de radiación
El vector de radiación es la superposición de ambos dipolos
G
N = N x xˆ + N y yˆ
El vector de radiación de un dipolo con distribución de corriente
sinusoidal para dipolos orientados en las direcciones x, y y con
corrientes desfasadas 90° es
1 − j π4 ⎛ cos k x H − cos kH ⎞
e ⎜
⎟
k 2 − k x2
2
⎝
⎠
1 j π4 ⎛ cos k y H − cos kH ⎞
N y = 2kI
e ⎜
⎟⎟
2
2
⎜
k
k
−
2
y
⎝
⎠
N x = 2kI
En coordenadas esféricas es
G
Nθ = N ⋅θˆ = ( N x xˆ + N y yˆ ) ⋅ ( cosθ cos φ xˆ + cosθ sin φ yˆ − sin θ zˆ )
G
Nφ = N ⋅ φˆ = ( N x xˆ + N y yˆ ) ⋅ ( − sin φ xˆ + cos φ yˆ )
Nθ = cos θ ( N x cos φ + N y sin φ )
Nφ = ( − N x sin φ + N y cos φ )
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
3
Campos radiados
G
µ e− jkr
ˆ
ˆ
E = − jω Aθθ + Aφφ = − jω
Nθθˆ + Nφ φˆ
4π r
(
)
(
)
Polarización
En la dirección z, se tiene la contribución de dos dipolos, ortogonales
con corrientes iguales en módulo y desfasadas 90o, la polarización es
circular
En el plano XY,
N θ = cos θ ( N x cos φ + N y sin φ ) = 0
N φ = ( −N x sin φ + N y cos φ )
Se puede observar que la polarización es lineal
Diagrama de radiación
El diagrama en el plano XY es
90
120
1
60
0.8
0.6
150
⎛π
EC⎜
⎝2
E1⎛⎜
⎝
π ⎞
,φ
2 ⎠
⎛π
⎝2
E2⎜
⎞
,φ
⎠
,φ
30
0.4
0.2
180
0
0
0
⎞
⎠
210
330
240
300
270
φ
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
4
DIAGRAMAS PLANO XZ
90
120
90
120
60
0.6
150
0.6
150
30
30
0.4
0.4
0.2
0.2
180
60
0.8
0.8
180
0
0
0
210
210
330
330
240
240
300
270
θ
Eφ
300
270
θ
Eθ
DIAGRAMAS TRIDIMENSIONALES
Eφ
Eθ
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia