Transformada bidimensional de aperturas
Anuncio
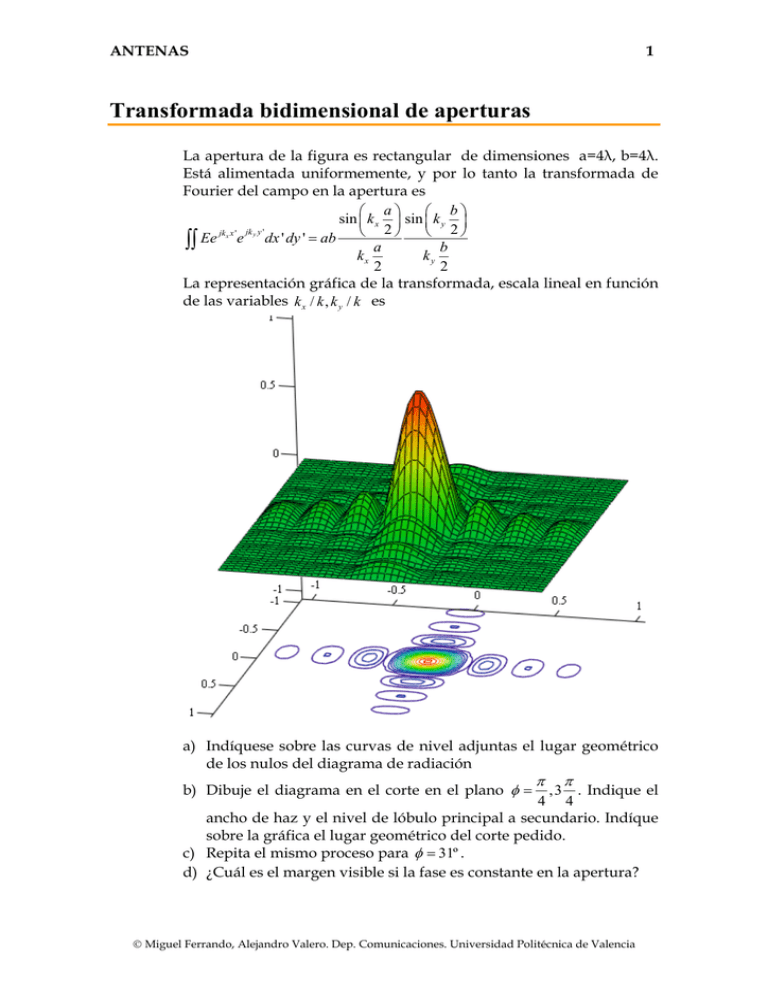
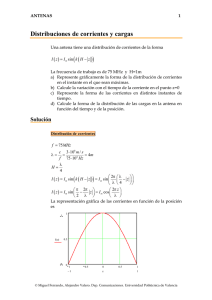
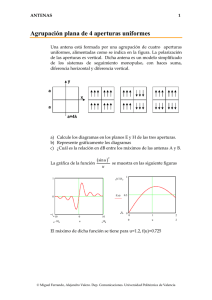
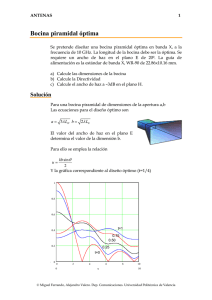
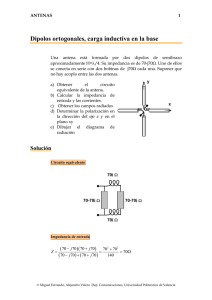
ANTENAS 1 Transformada bidimensional de aperturas La apertura de la figura es rectangular de dimensiones a=4λ, b=4λ. Está alimentada uniformemente, y por lo tanto la transformada de Fourier del campo en la apertura es ⎛ a⎞ ⎛ b⎞ sin ⎜ k x ⎟ sin ⎜ k y ⎟ jk x ' jk y y ' ⎝ 2⎠ ⎝ 2⎠ ∫∫ Ee x e dx ' dy ' = ab a b kx ky 2 2 La representación gráfica de la transformada, escala lineal en función de las variables k x / k , k y / k es a) Indíquese sobre las curvas de nivel adjuntas el lugar geométrico de los nulos del diagrama de radiación b) Dibuje el diagrama en el corte en el plano φ = π π . Indique el 4 4 ancho de haz y el nivel de lóbulo principal a secundario. Indíque sobre la gráfica el lugar geométrico del corte pedido. c) Repita el mismo proceso para φ = 31º . d) ¿Cuál es el margen visible si la fase es constante en la apertura? ,3 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 2 π G −j x e) ¿Cuál es el margen visible si los campos son E = Eo e λ Solución ⎛ a⎞ ⎛ b⎞ sin ⎜ k x ⎟ sin ⎜ k y ⎟ 2⎠ ⎝ 2 ⎠ = ab sin ( u ) sin ( v ) F ( k x , k y ) = ab ⎝ a b u v kx ky 2 2 a 2π = 2 λ b 2π v = ky = 2 λ u = kx 4λ sin θ cos φ = 4π sin θ cos φ 2 4λ sin θ sin φ = 4π sin θ sin φ 2 Como se puede observar u y v toman valores u ∈ [ −4π , 4π ] v ∈ [ −4π , 4π ] Los nulos se tienen para u, v = nπ n = ±1, ±2, ±3, ±4 El lugar geométrico son las rectas indicadas en la figura. ky k kx k © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 3 Corte a 450 El corte del diagrama se puede obtener particularizando el valor del ángulo a 2 k x = 2λ k sin θ cos φ = 4π sin θ 2 2 b 2 v = k y = 2λ k sin θ sin φ = 4π sin θ 2 2 u= Se puede observar que u = v ∈ ⎡⎣ −2 2π , 2 2π ⎤⎦ ( ) 2 ⎛ sin 2 2π sin θ ⎞ ⎟ F ( k x , k y ) = 16λ 2 ⎜ ⎜ 2 2π sin θ ⎟ ⎝ ⎠ El diagrama es el mismo que tendría una distribución triangular de dimensiones equivalentes a la diagonal de la apertura. La relación de lóbulo principal a secundario es 26.4 dB. El ancho de haz a –3dB es 130 Corte a 310 El diagrama corresponde a v sin φ = = tan φ u cos φ v = 0.6u El lugar geométrico es el segmento indicado en la figura. Los ceros del diagrama corresponden a las intersecciones con la rejilla, es decir los valores indicados en la figura con puntos, que corresponden a u = ±π v = ±π u = ±2π u = ±3π El margen visible sobre el segmento va desde u ∈ [ −4π cos φ , 4π cos φ ] v ∈ [ −4π sin φ , 4π sin φ ] © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 4 Diagrama de radiación a 310 El diagrama se puede representar de forma aproximada a partir de la posición de los ceros.La representación gráfica para 00,310,y 450 es 1 1 0.5 f ( θ , 0.01deg) f ( θ , 31 ⋅deg) f ( θ , 45 ⋅deg) 0 − 0.217 0.5 1.5 1 −π 0.5 0 0.5 1 θ 2 1.5 π 2 Margen visible de la apertura El margen visible es el conjunto de valores que corresponden a direcciones del espacio reales. En el caso de la apertura indicada como se ha demostrado es un círculo de radio 4π Efecto de una fase lineal Si se añade una fase lineal a la apertura, aparece un desplazamiento en la transformada, en la dirección del eje x ∫∫ E e o π λ −j x ⎛⎛ π ⎞a⎞ b sin ⎜ ⎜ k x − ⎟ ⎟ sin ⎛⎜ k y ⎞⎟ λ ⎠2⎠ ⎝ 2⎠ jk y ' ⎝⎝ e jkx x 'e y dx ' dy ' = ab b π ⎞a ⎛ ky ⎜ kx − ⎟ 2 λ⎠2 ⎝ Se puede observar que hay un desplazamiento del margen visible de valor 2π . El nuevo margen visible será un círculo desplazado. El centro está en u= 2π ,v=0. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia