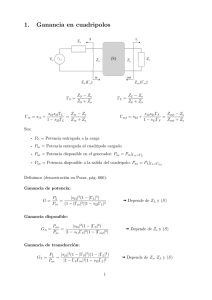
Obtener la matriz de scattering de una susceptancia jB en paralelo
Anuncio

Obtener la matriz de scattering de una susceptancia jB en paralelo, respecto a impedancias de las líneas de acceso Z0 ohmios. Puerta 1 Z0 V1 jB V2 Z0 Puerta 2 Solución: Los planos de referencia (z=0) se toman sobre la propia susceptancia. El parámetro S11 es el coeficiente de reflexión en la puerta 1 con la puerta 2 adaptada, lo que significa colocar una impedancia igual a la impedancia característica de la línea de acceso. Es decir, Z0 jB Z0 Trabajando con admitancias, S11 = donde Y0 = 1 S11 = V1− V1+ v2+ = 0 Z0 V1− V1+ = v2+ = 0 Y0 − Yin Y0 − ( jB + Y0 ) − jB = = = S22 Y0 + Yin jB + 2Y0 jB + 2Y0 . También se puede hacer con impedancias, −1 Z0 Z0 − Z0 − jBZ0 2 ⎛ 1 + jB ⎞ − Z − Z 0 ⎟ 0 Z − Z0 ⎜⎝ Z0 1 + jBZ0 1 + jBZ0 ⎠ = in = = = −1 Z0 Z0 + Z0 + jBZ0 2 Zin + Z0 ⎛ 1 ⎞ + Z 0 ⎜ Z + jB ⎟ + Z0 1 + jBZ 1 + jBZ0 0 ⎝ ⎠ 0 − jBZ0 = = S 22 2 + jBZ0 El parámetro S21 es S 21 = V2− V1+ . Se cumple que V1 = V1+ + V1− y V2 = V2+ + V1− = V1− , V2+ = 0 y como V1 = V2 (pues es un elemento en paralelo) entonces V1+ + V1− = V2− . Por tanto V2− S 21 = + V1 V2+ = 0 V1− = 1+ + V1 = 1 + S11 = V2+ = 0 2Y0 2 = 2Y0 + jB 2 + jBZ 0 Hemos calculado los parámetros de scattering respecto a tensiones reales. Como las impedancias de referencia de las líneas de las líneas de acceso son iguales, los parámetros obtenidos coinciden con los que se obtendrían respecto a tensiones normalizadas. Por lo tanto, al ser el sistema recíproco se tendrá que S 21 = S12 , como puede fácilmente comprobarse. Además, como el circuito no tiene pérdidas podemos comprobar que S11 + S 21 = 1 2 2