Modelos de Probabilidad y Muestreo
Anuncio
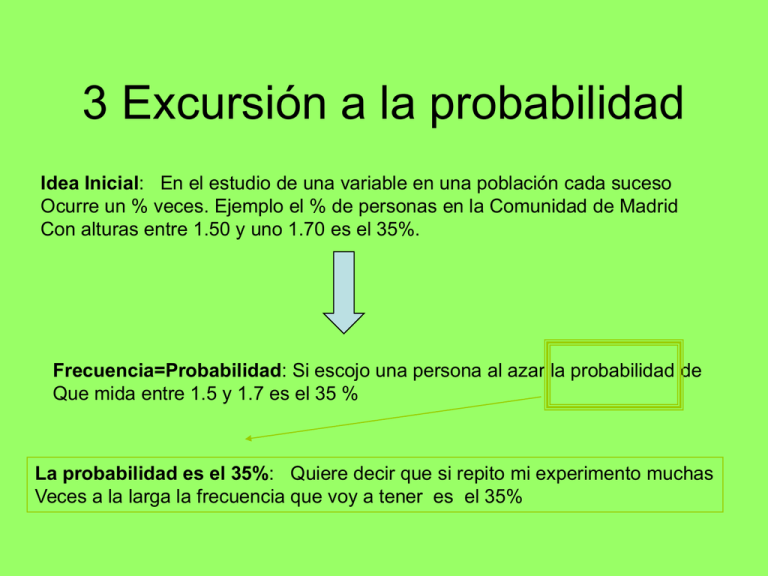
3 Excursión a la probabilidad Idea Inicial: En el estudio de una variable en una población cada suceso Ocurre un % veces. Ejemplo el % de personas en la Comunidad de Madrid Con alturas entre 1.50 y uno 1.70 es el 35%. Frecuencia=Probabilidad: Si escojo una persona al azar la probabilidad de Que mida entre 1.5 y 1.7 es el 35 % La probabilidad es el 35%: Quiere decir que si repito mi experimento muchas Veces a la larga la frecuencia que voy a tener es el 35% Guion 3.1 Conceptos básicos 3.2 Modelos de Probabilidad mas importantes V.Discreta Conozco los datos de toda la población. Por ejemplo numero de hijos en la comunidad de Madrid. P: ¿Cuál sera la probabilidad de tener dos hijos, 3 hijos, etc? Definición: Una variable aleatoria X decimos que es de tipo discreto cuando puede tomar los valores x i ,...., xk con probabilidades P( x i ), P(xk ). Estas probabilidades reciben el nombre de función de masa o función de probabilidad Nota 1: Las probabilidades son la modelización de las frecuencias relativas Nota 2: Las probabilidades son numeros entre 0 y 1 Nota 3: La suma de las probabilidades es 1 Nota 4: En los modelos de probabilidad la población es in finita Ejemplos: Urna, dado, Moneda, pesca Análogos a la media y varianza muestral Definición: La media o esperanza de X se define como k E[ X ] xi P( xi ) i 1 Definición: La varianza de X se define como k k i 1 i 1 2 V [ X ] ( xi E[ X ]) 2 P( xi ) ( xi ) 2 P( xi ) E[ X ]2 Definición: Una prueba de Bernoulli es un experimento aleatorio cuyos posibles resultados son agrupados en dos conjuntos excluyentes que llamaremos exito (E) y fracaso (F) con P(E)=p y P(F)=1-p ¿Cuál es la esperanza? ¿Cuál es la varianza? Importante: Diversas variables aleatorias pueden tener la misma distribución. ¿Ej lanzar una moneda o responder si o no? X B (1, p ) Parámetro V. Continua Conozco los datos de toda la población. Por ejemplo la altura en la comunidad de Madrid. La primera manera de describirlo es el histograma de paso 0.5 ¿Cómo lo hago mas preciso? Vario el paso ahora es 0.1. Siguiente 0.01………. En el limite el histograma aproxima Una curva ¿Dada la curva, como calculo la frecuencia(la probabilidad? Definición: Una variable aleatoria X decimos que es de tipo continuo cuando puede tomar cualquier valore en la recta real con una función de densidad f(x) Propiedades de la función de densidad f ( x) 0 P ( X I ) f ( x )dx I f ( x) 1 Definición: La media o esperanza de X se define como E[ X ] xf ( x )dx R Definición: La varianza de X se define como V [ X ] ( x E[ X ]) f ( x )dx ( x ) f ( x )dx E[ X ]2 2 2 R 2 R Modelos de Probabilidad mas importantes Modelo Binomial: Numero de exitos en n pruebas de Bernoulli independientes X B ( n, p ) n! x n x P( X x ) p (1 p) x ! n x ! ¿Para Calcular los estadisticos de la Binomial? Sean X i variables aleatorias independientes a) E[X1 X 2 ...... X n ] E[ X 1 ] E[ X 2 ] ...... E[ X n ] b)V [X1 X 2 ...... X n ] V [ X 1 ] V [ X 2 ] ...... V [ X n ] Xi E[X]=np 1 si Éxito en la prueba i-esima 0 si Éxito en la prueba i-esima n B ( n; p ) X i i 1 V[X]=np(1-p) Distribución de Poisson Límite de la distribución binomial B(n; p ) P( ) n np P( X x ) e X=0,1,2,…. E[X]=λ=V(X) x x! 0 Poisson 2 • ¿Es una función de masa? p 0,1 • En la práctica,¿ cuando son buenos los límites? n 30 p 0,1 np 10 • Numero de erratas en un libro, numero de Asegurados, etc La distribución Normal Su función de densidad 1 f ( x) e 2 1 x 2 ( ) 2 X N (, ) Propiedades 1. 2. 3. E[ X ] V(X ) 2 Es una densidad simétrica respecto a P( X 1) P ( X 1) 4. X N (, ) X N (0,1) Crucial para calcular probabilidades! 5. Límite de la distribución binomial n B(n; p ) N (np, np(1 p)) con p fijo! 0,1 p 0,9 n 30 6. X 1 N ( 1 , 1 ), X 2 N ( 2 , 2 ),......, X n N ( n , n ) X 1 X 2 ..... X n N ( 1 2 .... n , 1 2 ,...... n ) X 1 - X 2 N ( 1 2 , 1 2 ,...... n )