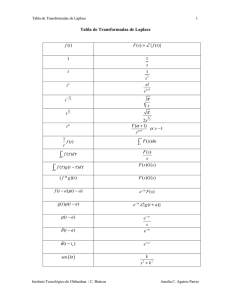
Anexo D Tabla de Integrales

Anexo D
Tabla de Integrales
(PUEDE SUMARSE UNA CONSTANTE ARBITRARIA A CADA INTEGRAL)
Z
xn dx =
1.
Z
2.
1
xn+1
n+1
(n 6= −1)
1
dx = log | x |
x
Z
ex dx = ex
3.
Z
ax dx =
4.
ax
log a
Z
5.
sen x dx = − cos x
Z
6.
cos x dx = sen x
Z
7.
tan x dx = − log |cos x|
Z
8.
cot x dx = log |sen x|
Z
9.
¯
¶¯
µ
¯
¯
1
1
x + π ¯¯
sec x dx = log |sec x + tan x| = log ¯¯tan
2
4
227
228
Tabla de Integrales
Z
10.
¯
¯
¯
1 ¯¯
¯
csc x dx = log |csc x − cot x| = log ¯tan x¯
2
Z
11.
arcsen
x
x √ 2
dx = x arcsen
+ a − x2
a
a
arccos
x
x √
dx = x arccos − a2 − x2
a
a
arctan
¡
¢
x
x a
dx = x arctan − log a2 + x2
a
a 2
Z
12.
Z
13.
Z
14.
(a > 0)
sen2 mx dx =
1
(mx − sen mx cos mx)
2m
cos2 mx dx =
1
(mx + sen mx cos mx)
2m
Z
15.
(a > 0)
(a > 0)
Z
sec2 x dx = tan x
16.
Z
csc2 x dx = −cot x
17.
Z
Z
senn−1 x cos x n − 1
sen x dx = −
senn−2 x dx
+
n
n
Z
cosn−1 x sen x n − 1
n
cos x dx =
+
cosn−2 x dx
n
n
Z
tann−1 x
n
tan x dx =
− tann−2 x dx (n 6= 1)
n−1
Z
cotn−1 x
n
cot x dx =
− cotn−2 x dx (n 6= 1)
n−1
Z
tan x secn−2 x n − 2
n
+
secn−2 x dx (n 6= 1)
sec x dx =
n−1
n−1
Z
cot x csc n−1 x n − 2
n
csc x dx =
+
cscn−2 x dx (n 6= 1)
n−2
n−1
n
18.
Z
19.
Z
20.
Z
21.
Z
22.
Z
23.
Z
24.
senh x dx = cosh x
Z
25.
cosh x dx = senh x
229
Z
26.
tanh x dx = log |cosh x|
Z
27.
coth x dx = log |sen hx|
Z
28.
sech x dx = arctan (senh x)
Z
29.
Z
30.
Z
31.
¯
x ¯¯
1
cosh x + 1
¯
csch x dx = log ¯tanh ¯ = − log
2
2
cosh x − 1
1
1
senh2 x dx = senh 2x − x
4
2
1
1
cosh2 x dx = senh 2x + x
4
2
Z
sech2 x dx = tanh x
32.
Z
x
x √
dx = xsenh−1 − x2 − a2 (a > 0)
a
a
√
£
¡ ¢
¤
½
Z
xcosh−1 xa − √x2 − a2 £cosh−1 ¡ xa ¢ > 0, a > 0¤
−1 x
34.
cosh
dx =
xcosh−1 xa + x2 − a2 cosh−1 xa < 0, a > 0
a
Z
¯
¯
x
x a
35.
tanh−1 dx = xtanh−1 + log ¯a2 − x2 ¯
a
a 2
Z
³
´
√
x
1
√
36.
dx = log x + a2 + x2 = sen h−1
(a > 0)
a
a2 + x2
Z
1
1
x
37.
dx = arctan
(a > 0)
2
2
a +x
2
a
Z √
x
x√ 2
a2
38.
(a > 0)
a2 − x2 dx =
a − x2 + arcsen
2
2
a
Z
¢√
¡ 2
¢3
x
x¡ 2
3a4
5a − 2x2
arcsen
(a > 0)
39.
a − x2 2 dx =
a 2 − x2 +
8
8
a
Z
1
x
√
40.
(a > 0)
dx = arcsen
a
a2 − x2
¯
¯
Z
¯a + x¯
1
1
¯
dx =
log ¯¯
41.
a2 − x2
2a
a − x¯
33.
senh−1
230
Tabla de Integrales
Z
42.
1
(a2 − x2 )
Z √
3
2
dx =
a2
√
x
a2 − x2
¯
¯
√
x√ 2
a2
¯
¯
2
2
2
43.
± dx =
x ± a ± log ¯x + x ± a ¯
2
2
Z
¯
¯
√
x
1
¯
¯
√
dx = log ¯x + x2 − a2 ¯ = cosh−1
(a > 0)
44.
a
x2 − a 2
¯
¯
Z
¯ x ¯
1
1
¯
¯
45.
dx = log ¯
x(a + bx)
a
a + bx ¯
Z
x2
a2
√
3
2 (3bx − 2a) (a + bx) 2
46.
x a + bx dx =
15b2
Z
Z √
√
1
a + bx
√
47.
dx = 2 a + bx + a
dx
x
x a + bx
√
Z
x
2 (bx − 2a) a + bx
√
48.
dx =
3b2
a + bx
¯√
¯

¯ a+bx−√
a¯
Z

√1 log ¯ √
√
¯ (a > 0)
1
a
a+bx+
q a
√
dx =
49.
 √2 arctan a+bx (a > 0)
x a + bx
−a
−a
Z √
50.
Z
51.
√
¯
¯
√
¯ a + a2 − x2 ¯
a2 − x2
¯
dx = a2 − x2 − a log ¯¯
¯
x
x
√
¢3
1¡
x a2 − x2 dx = − a2 − x2 2
3
Z
√
¢√
x¡ 2
a4
x
x2 a2 − x2 dx =
2x − a2
a2 − x2 + arcsen
8
8
a
√
¯
¯
Z
¯ a + a 2 − x2 ¯
1
1
¯
¯
√
53.
dx = − log ¯
¯
a
x
x a2 − x2
Z
√
x
√
54.
dx = − a2 − x2
a2 − x2
Z
x2
x√ 2
x
a2
√
55.
dx = −
(a > 0)
a − x2 + arcsen
2
2
2
2
a
a −x
¯
¯
Z √ 2
¯ a + √x2 + a2 ¯
√
x + a2
¯
¯
56.
dx = x2 + a2 − a log ¯
¯
¯
¯
x
x
52.
(a > 0)
231
Z √
57.
³x´
√
√
x2 − a 2
a
dx = x2 − a2 − a arccos
= x2 − a2 − arcsec
x
|x|
a
(a > 0)
Z
√
¢3
1¡ 2
x x2 ± a2 dx =
x ± a2 2
3
¯
¯
Z
¯
¯
x
1
1
¯
√
√
59.
dx = log ¯¯
a
x x2 + a2
a + x2 + a2 ¯
Z
1
1
a
√
60.
dx = arccos
(a > 0)
a
|x|
x x2 − a 2
√
Z
1
x2 ± a2
√
61.
dx = ±
a2 x
x2 x2 ± a2
Z
√
x
√
62.
dx = x2 ± a2
x2 ± a 2
¯
¯
(
√
Z
¯ 2ax+b−√
b2 −4ac ¯
√ 1
log
1
¯
¯ (b2 > 4ac)
b2 −4ac
2ax+b+ b2 −4ac
63.
dx
=
ax2 + bx + c
√ 2
arctan √2ax+b
(b2 < 4ac)
4ac−b2
4ac−b2
Z
Z
¯ 2
¯
x
1
b
1
¯
¯
64.
dx =
log ax + bx + c −
dx
2
2
ax + bx + c
2a
2a
ax + bx + c
(
√ √
Z
√1 log |2ax + b + 2 a ax2 + bx + c| (a > 0)
1
a
√
dx =
65.
−2ax−b
√1 arcsen √
(a < 0)
ax2 + bx + c
−a
b2 −4ac
58.
Z √
Z
2ax + b √ 2
4ac − b2
1
√
66.
+ bx + c dx =
ax + bx + c +
dx
4a
8a
ax2 + b + c
√
Z
Z
x
ax2 + bx + c
b
1
√
√
67.
dx =
−
dx
2
2
a
2a
ax + bx + c
ax + bx + c
¯ √√ 2
¯
(
Z
¯ 2 c ax +bx+c+bx+2c ¯
−1
√
log
1
¯
¯ (c > 0)
x
c
√
dx =
68.
bx+2c
√1 arcsen
√
(c < 0)
x ax2 + bx + c
−c
|x| b2 −4ac
ax2
µ
¶q
1 2
2 2
69.
x
+ dx =
x − a
(a2 + x2 )3
5
15
q
Z √ 2
2
∓
(x2 ± a2 )3
x ±a
dx =
70.
x4
3a2 x3
Z
sen(a − b)x sen(a + b)x
71.
sen ax sen bx dx =
−
2(a − b)
2(a + b)
Z
3
√
x2
a2
¡
a2 6= b2
¢
232
Tabla de Integrales
Z
72.
sen ax cos bx dx =
cos(a − b)x cos(a + b)x
−
2(a − b)
2(a + b)
¡
cos ax cos bx dx =
sen(a − b)x sen(a + b)x
−
2(a − b)
2(a + b)
¡
Z
73.
a2 6= b2
¢
a2 6= b2
¢
Z
74.
sec x tan x dx = sec x
Z
75.
csc x cot x dx = −csc x
Z
Z
cosm−1 x senn−1 +x m − 1
+
cosm−2 x senn x dx =
cos x sen x dx =
m+n
m+nZ
senn−1 x cosm+1 x
n−1
= −
+
cosm x senn−2 x dx
m+n
m+n
Z
n
1 n
n
xn−1 cos ax dx
x sen ax dx = − x cos ax +
a
a
Z
1 n
n
n
x cos ax dx = x sen ax −
xn−1 sen ax dx
a
a
Z
xn eax n
n ax
x e dx =
−
xn−1 eax dx
a
a
·
¸
1
n
n+1 log ax
x log(ax) dx = x
−
n+1
(n + 1)2
Z
xn+1
m
m
m
n
x (log ax) dx =
(log ax) −
xn (log ax)m−1 dx
n+1
n+1
m
76.
Z
77.
Z
78.
Z
79.
Z
80.
Z
81.
n
Z
82.
eax sen bx dx =
eax (a sen bx − b cos bx)
a2 + b2
eax cos bx dx =
eax (b sen bx + a cos bx)
a 2 + b2
Z
83.
Z
84.
sech x tanh x dx = −sech x
Z
85.
csch x coth x dx = −csch x