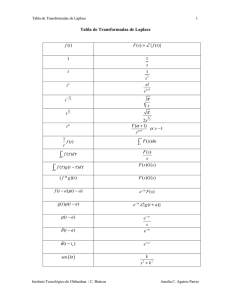
Tabla de Derivadas
Anuncio

TABLA DERIVADAS 1 2 3 4 5 6 7 8 9 10 11 12 Por: Fernando Valdés M ©, UTP, Pereira d (cu) = cu′ dx d (uvw) = u′ vw + uv ′ w + uvw′ dx d n (u ) = nun−1 u′ dx d (u + v) = u′ + v ′ dx d ( u ) vu′ − uv ′ = dx v v2 d u ′ |u| = u dx |u| d (uv) = u′ v + uv ′ dx d (c) = 0 dx d 1 ln(u) = u′ dx u d u (e ) = eu u′ dx d cos(u) = − sen(u) u′ dx d sec(u) = sec(u) tan(u) u′ dx d f (g(x)) = f ′ (g(x))g ′ (x) dx d sen(u) = cos(u) u′ dx d cos(ku) = − sen(ku)ku′ dx d cot(u) = − csc2 (u) u′ dx 1 d loga (u) = u′ dx u ln(a) d sen(ku) = cos(ku) ku′ dx d tan(u) = sec2 (u) u′ dx d csc(u) = − csc(u) cot(u) u′ dx d u a = au ln(a) u′ dx 1 d arc sen(u) = √ u′ dx 1 − u2 d senh(u) = cosh(u) u′ dx d sech(u) = −sech(u) tanh(u) u′ dx d 1 u′ senh−1 (u) = √ dx 1 + u2 d 1 sech−1 (u) = − √ u′ dx u 1 − u2 1 d arc cos(u) = − √ u′ dx 1 − u2 1 d arctan(u) = u′ dx 1 + u2 d cosh(u) = senh(u) u′ dx d csch(u) = −csch(u) coth(u) u′ dx d 1 u′ cosh−1 (u) = √ dx u2 − 1 d 1 csch−1 (u) = − √ u′ dx |u| 1 + u2 d tanh(u) = sech2 (u) u′ dx d coth(u) = −csch2 (u) u′ dx d 1 tanh−1 (u) = u′ dx 1 − u2 TRIGONOMETRÍA HIPERBÓLICA e +e ex − e−x senh(x) cosh(x) = senh(x) = tanh(x) = 2 2 cosh(x) 2 2 2 2 2 cosh (x) − senh (x) = 1 1 − tanh (x) = sech (x) coth (x) − 1 = csch2 (x) ( ) √ √ 1 1+x senh−1 (x) = ln(x + x2 + 1) cosh−1 (x) = ln(x + x2 − 1) tanh−1 (x) = ln 2 1−x −1 + cosh(2x) 1 + cosh(2x) senh2 (x) = cosh2 (x) = cosh(2x) = cosh2 (x) + senh2 (x) 2 2 −x x 1 2 3 4 2 2 TRIGONOMETRÍA CIRCULAR 1 + tan2 (x) = sec2 (x) sin(π − x) = sen(x), sen(2x) = 2 sen(x) cos(x) 1 − cos(2x) sen2 (x) = 2 cos(−x) = cos(x) sec(x) = 1/ cos(x) 5 6 sen (x) + cos (x) = 1 sen(x + π/2) = cos(x) cos(x + π/2) = sen(x) 2 tan(x) tan(2x) = 1 − tan2 (x) sen(−x) = − sen(x), csc(x) = 1/ sen(x), 7 tan(x) = 8 a sen(x) + b cos(x) = R sen(x + α) 9 a sen(x) + b cos(x) = R cos(x − α) 1 2 3 4 10 d 1 coth−1 (u) = u′ dx 1 − u2 sen −1 cos(x) cot(x) = sen(x) √ R = a2 + b2 =⇒ √ R = a2 + b2 =⇒ sen(x) cos(x) (x) + cos −1 =⇒ =⇒ tan−1 (x) + cot−1 (x) = π/2 (x) = π/2 1 1 + cot2 (x) = csc2 (x) sen(π/2 − x) = cos(x) cos(2x) = cos2 (x) − sen2 (x) 1 + cos(2x) cos2 (x) = 2 tan(−x) = − tan(x) cot(x) = 1/ tan(x) b a a tan(α) = b tan−1 (x) + tan−1 (1/x) = π/2 tan(α) =


![1. ∫ [u(x)] u (x)dx = r + 1 + C, r = −1 2. ∫ u∨(x) u(x) dx = ln|u(x)| + C](http://s2.studylib.es/store/data/008568496_1-96765d9c7bd315d4a548949875995ddd-300x300.png)