PROBLEMA RESUELTO No. 1 Solución:
Anuncio
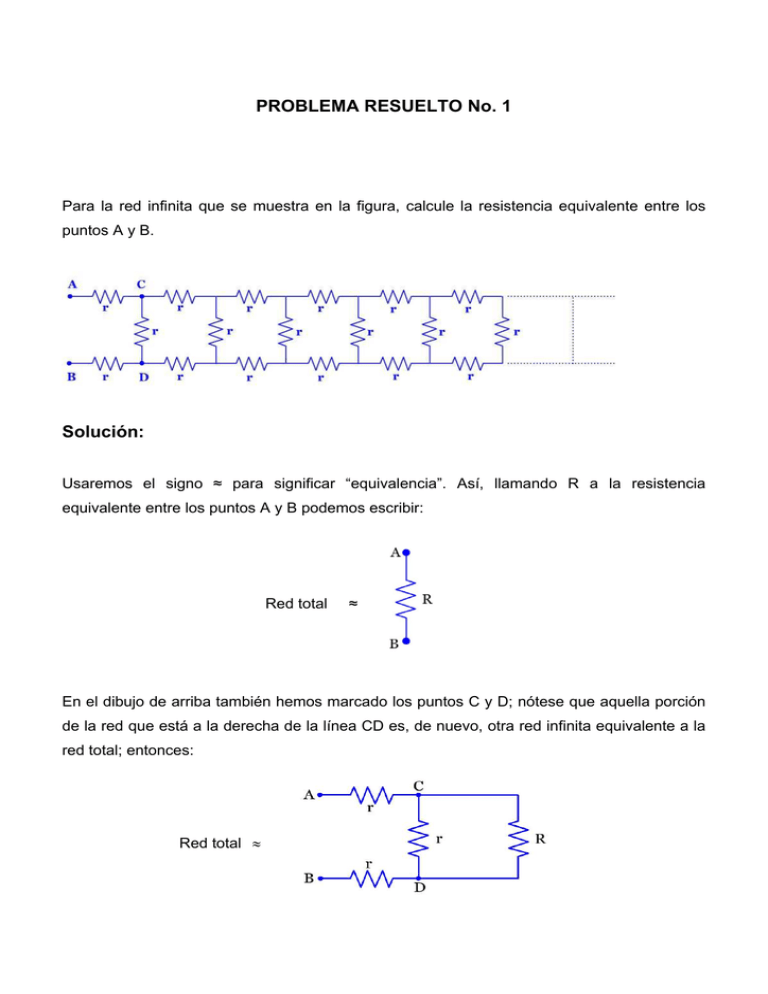
PROBLEMA RESUELTO No. 1 Para la red infinita que se muestra en la figura, calcule la resistencia equivalente entre los puntos A y B. Solución: Usaremos el signo ≈ para significar “equivalencia”. Así, llamando R a la resistencia equivalente entre los puntos A y B podemos escribir: Red total ≈ En el dibujo de arriba también hemos marcado los puntos C y D; nótese que aquella porción de la red que está a la derecha de la línea CD es, de nuevo, otra red infinita equivalente a la red total; entonces: Red total ≈ Obsérvese que R está en paralelo con una resistencia r, entonces: Red total ≈ Y éste es un circuito de tres resistencias en serie, entonces Red total ≈ Comparando (1) con (2) podemos escribir: R = 2r + rR , es decir r+R R 2 − 2rR − 2r 2 = 0 , de donde R = r (1 ± 3 ) ; Pero R debe ser > 0, y por consiguiente, R = r (1 + 3 ) .











