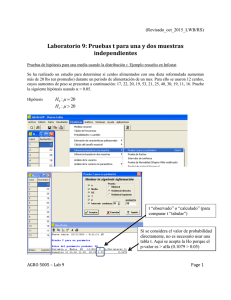
H μ = μ
Anuncio
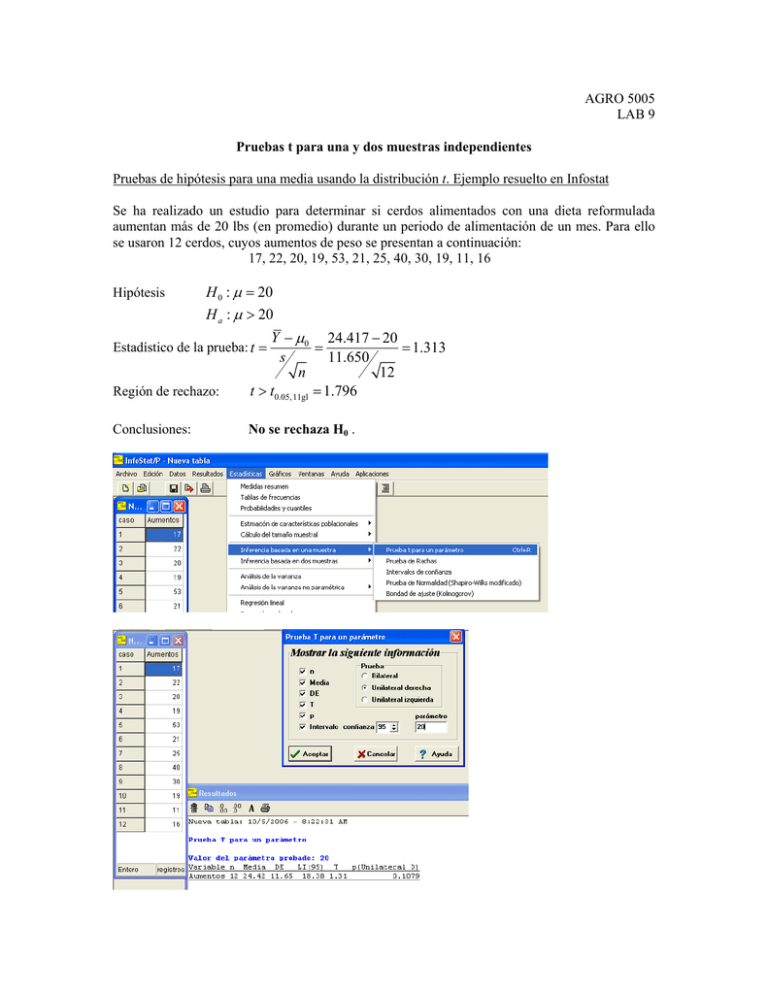
AGRO 5005 LAB 9 Pruebas t para una y dos muestras independientes Pruebas de hipótesis para una media usando la distribución t. Ejemplo resuelto en Infostat Se ha realizado un estudio para determinar si cerdos alimentados con una dieta reformulada aumentan más de 20 lbs (en promedio) durante un periodo de alimentación de un mes. Para ello se usaron 12 cerdos, cuyos aumentos de peso se presentan a continuación: 17, 22, 20, 19, 53, 21, 25, 40, 30, 19, 11, 16 Hipótesis H 0 : μ = 20 H a : μ > 20 Región de rechazo: Y − μ0 24.417 − 20 = = 1.313 s 11.650 n 12 t > t0.05, 11gl = 1.796 Conclusiones: No se rechaza H0 . Estadístico de la prueba: t = 1. Calcule las siguientes probabilidades usando la tabla t e InfoStat. Incluya un diagrama en cada caso. a. P(T>1.356) si gl=12 b. P(T<2.101) si gl=18 c. P(T<-1.319) si gl=23 d. P(T<-1.711) si gl=24 e. P(T<.697) si gl=11 2. Determine los valores críticos (valores en la tabla) de t, haga un diagrama de la distribución y lleve a cabo las pruebas indicadas. Calcule los valores p usando el calculador de probabilidad de Infostat (o el graficador). a. H 0 : μ = 30, H a : μ ≠ 30, n = 16, Y = 32, s 2 = 25, α = 0.05 b. H 0 : μ = 58, H a : μ < 58, n = 18, Y = 57, s 2 = 100, α = 0.05 c. H 0 : μ = 25, H a : μ < 25, n = 25, Y = 9, s 2 = 20, α = 0.05 d. H 0 : μ = 430, H a : μ ≠ 430, n = 10, Y = 400, s 2 = 14, α = 0.01 3. Los rendimientos de 7 plantas de piña aleatoriamente escogidas, variedad “Cabezona”, fueron 4.2, 5.6, 4.3, 4.8, 5.7, 5.5 y 4.9 kg/planta. (a) Construya un intervalo de confianza del 95% para la media poblacional. (b) Pruebe H0: μ=4.5, Ha: μ≠4.5 usando α=.05. (c) Repita los pasos 1 y 2 usando InfoStat. 4. Se condujo un experimento para examinar la susceptibilidad de raíces de cierta variedad de limonero a una larva específica. Cuarenta y un plantas se expusieron a la larva, y se examinaron luego de cierto tiempo. La respuesta de interés es el logaritmo del número de larvas por gramo encontradas en cada raíz. Para las 41 plantas estudiadas, la media muestral fue 9.02 y la desviación estándar 1.12. Pruebe la hipótesis que μ=10 versus μ<10 usando α=.01. Calcule el valor p usando InfoStat. Construya un intervalo de confianza del 95% para la susceptibilidad media de las raíces. 5. El tiempo que le toma a la habichuela en duplicar su peso es una medida de su calidad de enlatar (mientras más rápido, mejor). Un experimento con 15 repeticiones (independientes) de cada variedad produjo los resultados siguientes: Y = 17.2 horas, s=0.7 horas La Cuarentena: La Bonita: Y = 18.7 horas, s=0.8 horas (a) Conduzca una prueba para determinar cuál variedad tiene mejor calidad de enlatar. Use α=.05. (b) Pruebe si la variedad Bonita tiene peor calidad comparada con la Cuarentena. Use α=.05. 6. Usando los datos del laboratorio 2 (altura de plantas de café), pruebe si las alturas promedios son diferentes en las plantas sanas y en las plantas enfermas. Formule las hipótesis de interés y obtenga sus conclusiones usando α=.10. 7. Un inspector de control de contaminación sospechaba que una comunidad ribereña estaba descargando aguas servidas no-tratadas en el río y eso cambiaba el nivel de oxígeno disuelto en el río. Para probar esto, obtuvo 5 muestras aleatorias de agua del río en una zona río arriba del pueblo, y otras 5 muestras en una zona río abajo del pueblo. Se midieron los niveles de oxígeno disuelto, en ppm. ¿Proveen los datos evidencia de un contenido menor de oxígeno río abajo? Use α=.05. Río arriba: 4.8, 5.2, 5.0, 4.9, 5.1 Río abajo: 5.0, 4.7, 4.9, 4.8, 4.9 8. Un estudio se realizó en 16 vacas lecheras. Ocho vacas fueron asignadas aleatoriamente a un régimen de líquidos de agua solamente (grupo 1), y las otras recibieron suero líquido solamente (grupo 2). Además, a cada animal se le dio 7.5 kg de grano por día, y se le permitió comer heno a voluntad. Se registró, entre otras cosas, la cantidad de heno (en kg/vaca) consumido diariamente. Grupo 1: 15.1, 14.9, 14.8, 14.2, 13.1, 12.8, 15.5, 15.9 Grupo 2: 6.8, 7.5, 8.6, 8.4, 8.9, 8.1, 9.2, 9.5 (a) Pruebe la hipótesis que hay diferencias entre los consumos diarios promedios de heno en los dos grupos con α=.01. (b) ¿Cuáles son los supuestos necesarios para las pruebas realizadas en la parte a? Comente sobre su validez en este caso (grafique los datos si fuese necesario).