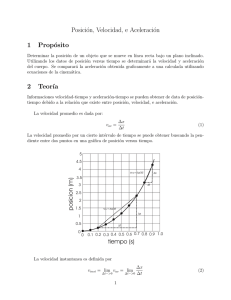
Figura 1: El sistema de la figura representa un
Anuncio

Figura 1: El sistema de la figura representa un mecanismo plano formado por las barras AB,BC,CD, de longitudes 2a, a, 2a respectivamente, articuladas entre sı́ en los puntos B,C y a dos puntos fijos A,D. Se considera el instante representado, en el que la barra BC es perpendicular a las barras AB y CD, tomándose un sistema cartesiano de referencia fijo con origen en A, ejes x e y según las direcciones y sentidos de los vectores AB, BC en el instante inicial y eje z en sentido saliente del plano. La barra AB se mueve con velocidad angular constante ω. 1. Obtenga, en la referencia definida, las velocidades de B y C, ası́ como las rotaciones de las barra BC, CD. Evidentemente, v B = 2ωaj y por el teorema de las velocidades proyectadas v C = 2ωaj con lo que la rotación de la barra BC es nula ω BC = 0 Además, a partir de la velocidad de C, se tiene ω CD = −ωk 2. Halle la aceleración de B. aB = −2ω 2 ai 3. Formule el teorema de las velocidades proyectadas para los puntos B y C, derı́velo y obtenga una fórmula similar para las aceleraciones de B y C, de la que deducir la aceleración angular de la barra CD y la aceleración de C. De la ecuación v B · BC = v C · BC 1 se tiene aB · BC + v B · (ω BC × BC) = aC · BC + v C · (ω BC × BC) con lo que aB · BC = aC · BC 0 = −2a2 ω̇CD ⇒ ω̇CD = 0 y la aceleación de C es aC = 2ω 2 ai 4. Sea P el punto medio del segmento BC. Obtenga su velocidad, aceleración y curvatura de su trayectoria. Su velocidad y aceleración son las medias de las de B y C, por lo que se tiene v P = 2ωi aP = 0 su curvatura, por la segunda ecuación intrı́seca de la aceleración, será nula. 5. Sean ϕ1 , ϕ2 los ángulos girados en sentido antihorario y horario respectivamente por los segmentos AB, CD desde la posición referida anteriormente. Muestre que si ϕ2 = f (ϕ1 ), entonces f (0) = 0 ∧ f 0 (0) = 1 ∧ f 00 (0) = 0 ∧ x = −f (−f (x)) Las primeras ecuaciones se deducen de los apartados anteriores. La cuarta refleja la simetrı́a del sistema. De hecho, la función es f (x) = arccos( 6 − sen (x) − 4 cos(x) 1 − 2sen (x) ) − arctan( ); 1/2 4 − 2 cos(x) (21 − 4sen (x) − 16 cos(x)) 6. Deduzca que f 000 (0) = 0 De x = −f (−f (x)) se tiene 1 = f 0 (−f (x))f 0 (x) 0 = −f 00 (−f (x))f 02 (x) + f 0 (−f (x))f 00 (x) 0 = f 000 (−f (x))f 03 (x) − 3f 00 (−f (x))f 0 (x)f 00 (x) + f 0 (−f (x))f 000 (x) con lo que f 000 (0) = 0 2 7. Sea r P (t) = x(t)i + y(t)j el vector de posición de P. Demuestre que x000 (0) = 0. La sobre aceleración de P es la media entre las sobre aceleraciones de B y C, por lo que saB = −2aω 3 j saC = −2aω 3 j con lo que x000 (0) = 0 8. Sea r P (t) = a(`)i+b(`)j el vector de posición de P en función de la abscisa curvilı́nea de su trayectoria, con origen en la posición señalada y sentido positivo hacia arriba. Demuestre que las derivadas de orden par de a en ` = 0 son nulas. Dada la antisimetrı́a de la curva, se sigue inmediatamente. 9. Obtenga las derivadas en el origen de hasta tercer orden de a(`) y la de cuarto orden de x(t), relacionando estas funciones, en función de `(t). x0 (t) = a0 (`(t))`0 (t) ⇒ a0 (0) = 0 x00 (t) = a00 (`(t))`0 (t) + a0 (`(t))`00 (t) ⇒ a00 (0) = 0 como podı́a predecirse. x000 (t) = a000 (`(t))`0 (t) + 2a00 (`(t))`00 (t) + a0 (`(t))`000 (t) ⇒ a000 (0) = 0 x0000 (t) = a0000 (`(t))`0 (t)+3a000 (`(t))`00 (t)+3a00 (`(t))`000 (t)+a0 (`(t))`0000 (t) ⇒ x0000 (0) = 0 Es decir, existe un contacto de al menos orden cuatro entre la trayectoria de P y la recta soporte de la posición inicial del segmento BC. 10. Se completa el mecanismo con otros tres segmentos: AE de longitud a, CE y BF de longitud 2a; Los segmentos AE y BF se articulan en sus extremos, mientras que el segmento CE se une rı́gidamente en C al CD, prolongándolo y se articula en E, como muestra la figura, de forma que los puntos F, B, E, C forman siempre un paralelogramo. Demuestre que la velocidad de F siempre es el doble que la de P. Por el teorema de Tales, F siempre se encuentra en la lı́nea que une D con P a una distancia doble que P, por lo que, tomando origen en D, el vector de posición de F es el doble que el de P. La trayectoria de F también tiene un contacto de orden cuarto con una recta paralela a la posición inicial del segmento BC. 3 Figura 2: 4