Boletín 1
Anuncio

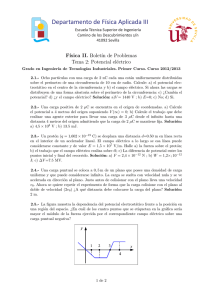
Departamento de Física Aplicada III Escuela Técnica Superior de Ingeniería Grado en Ingeniería de Organización Industrial Física II Boletı́n 1: Fuerzas eléctricas y campo eléctrico 1.1.- Dos partı́culas cargadas con cargas q iguales y de signo contrario se encuentran separadas por una distancia d. Sobre la recta que las une se coloca una nueva partı́cula con carga positiva, q , a una distancia d de la carga −q. ¿Qué valor ha de tener q para que la fuerza neta sobre la carga positiva q sea nula? Solución: q = 4q d d + - + q -q q’ x 1.2.- Dos partı́culas con carga q1 = q2 = 1μC se encuentran situadas en las posiciones r1 = di y r2 = d j donde d= 1 m. Se coloca una tercera partı́cula con carga q3 = 2μC en r3 = d(i + j). a) calcular la fuerza sobre q3 , b) +Qué valor ha de tener una carga q4 situada en el origen para que la fuerza neta√ sobre la partı́cula con carga q3 pase a ser nula? Solución: a) Ft = 18× 10−3 (ı +j) N; b) q4 = −2 2 μC 1.3.- Dos cargas puntuales positivas e iguales se colocan sobre el eje x separadas por una distancia 2d, de forma que el origen de coordenadas coincide con el punto medio entre las dos cargas. Calcule: a) El campo eléctrico sobre un punto cualquiera del eje y. b) Si las cargas tienen un valor de 1 nC y d =1 cm, calcular el campo eléctrico para y=0, y=1 cm e y=10 cm. c) Comparar con el campo que crearı́a en esos mismos puntos una carga de 2 nC situada = 2kqy(d2 + y 2 )−3/2j; b) E(y=0) = 0; E(y=1 en el origen de coordenadas. Solución: a) E cm)=63.6 × 103 N/C; E(y=10 cm)=17.7 × 102 N/C; c) E(y=0) = ∞; E(y=1 cm)=18 × 104 N/C; E(y=10 cm)=18 × 102 N/C. 1.4.- Una carga Q se distribuye uniformemente sobre un anillo de radio a. Calcule el campo eléctrico en un punto situado sobre el eje del anillo a una distancia x de su centro. Solución: = kQx(x2 + a2 )−3/2 ı E 1.5.- Un anillo de radio a se encuentra en el plano x = 0 situado de tal forma que el eje x pasa por su centro. El anillo posee una carga Q que se distribuye uniformemente sobre su longitud. a) Partiendo del resultado del problema anterior, demostrar que el campo eléctrico creado por el anillo en un punto x del eje es proporcional a x cuando x a. b) Se coloca en el centro del anillo una partı́cula de masa m y carga -q. Demostrar que si desplazamos ligeramente la partı́cula en la dirección del eje x, ésta experimenta un movimiento armónico simple.c) Calcular el periodo de dicho movimiento oscilatorio. Solución: a) Ex = kQx/a3 ; c) T = 2π ma3 /kQq. 1 1.6.- Halle el campo eléctrico que produce un disco de radio R con una densidad superficial de carga uniforme y positiva σ en un punto a lo largo del eje del disco situado a una distancia x de su centro. +Puede obtener a partir de esta expresión el campo de una lámina plana infinita de 2 2 −1/2 = 2πkσı i; Para el plano de carga: E carga? Solución: E = 2πkσ 1 − x(x + R ) 1.7.- Una carga Q se distribuye uniformemente en la superficie de una esfera de radio R. Calcular el campo eléctrico dentro y fuera de la esfera. Solución: Er = kQ/r 2 si r > R y Er = 0 si r < R. 1.8.- En el interior de una esfera de radio R que posee una carga Q uniformemente distribuida en su volumen se taladra un hueco esférico de radio R/2 tal como muestra la figura. Calcular P = 7k Q2 ı; E P = k Q2 ı; E P = el campo eléctrico en los puntos P1 , P2 y P3 . Solución: E 1 2 3 36 R 2R 3k Q − 8 R2 ı. y R P3 2R P2 R/2 P1 x R/2 1.9.- Un cilindro de radio a y cuya longitud puede considerarse infinita alberga una densidad de carga uniforme ρ. Calcular el campo eléctrico en todos los puntos del espacio. Solución: ρa2 ρr ; r < a: Er = 2ε r > a: Er = 2ε 0r 0 1.10.- Sobre una superficie plana (plano z=0) que puede considerarse infinita se ha depositado una densidad superficial de carga uniforme, σ. a) Calcule el campo eléctrico a ambos lados del plano. b) Se dispone ahora otro plano con densidad superficial de carga -σ paralelamente al primero en z = d. Halle el campo en todos los puntos del espacio. Solución: a) Ez = σ/(2ε0 ) para z > 0 y Ez = −σ/(2ε0 ) para z < 0; b) Ez = σ/ε0 para 0 < z < d, E = 0 en otro caso. 2