TEMA 3 TRABAJO Y ENERGÍA CONSEJOS PREVIOS A

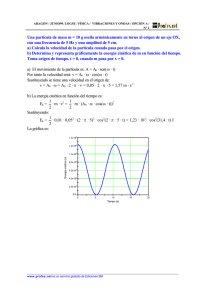
TEMA 3
TRABAJO Y ENERGÍA
CONSEJOS PREVIOS A LA RESOLUCION DE LOS PROBLEMAS
Trabajo y energía cinética
A la hora de resolver un problema de trabajo y energía cinética, escoge las
posiciones inicial y final del cuerpo y dibuja un diagrama del cuerpo libre con todas las
fuerzas que actúan sobre él. Lista las fuerzas y calcula el trabajo efectuado por cada una.
Una o más de las fuerzas pueden desconocerse; representa las incógnitas con símbolos
algebraicos. Revisa los signos. Si una fuerza tiene una componente en la dirección del
desplazamiento, su trabajo es positivo; si tiene una componente opuesta al desplazamiento,
su trabajo es negativo. Si la fuerza y el desplazamiento son perpendiculares, el trabajo es
nulo.
Suma el trabajo realizado por las fuerzas individuales para obtener el trabajo
total. Cuida los signos. A veces puede ser más fácil obtener primero la suma vectorial de las
fuerzas (fuerza neta) y luego calcular el trabajo de la fuerza neta.
Escribe expresiones para la energía cinética inicial y final (ECi y ECf). Si desconoces
una cantidad como vi o vf, exprésala con su símbolo algebraico. Al calcular las energías
cinéticas asegúrate de usar la masa del cuerpo, no su peso.
Usa la relación Wtotal=ECf-ECi=∆EC; inserta los resultados de los pasos anteriores y
despeja la incógnita requerida. Recuerda que la energía cinética nunca puede ser negativa.
Si obtienes una energía cinética negativa cometiste un error. Tal vez intercambiaste los
subíndices i y f, o tuviste un error de signo en uno de los cálculos del trabajo.
Energía potencial y conservación de la energía
Decide primero si conviene resolver el problema con métodos de energía, usando
ΣF=ma directamente, o con una combinación. El primer enfoque es muy útil si el problema
implica movimiento con fuerzas variables, en una trayectoria curva o ambas cosas. Si el
problema implica tiempo transcurrido el enfoque de energía no suele ser el mejor porque en
él no interviene el tiempo directamente.
Si usas el enfoque de la energía, decide primero cuáles son los estados inicial y final
(posiciones y velocidades) del sistema. Usa el subíndice 1 para el estado inicial y 2 para el
final. Es útil preparar dibujos que muestren los estados inicial y final.
Define tu sistema de coordenadas, sobre todo el nivel en el que y=0. Esto te servirá
para calcular las energías potenciales gravitatorias. La ecuación EPg=mgy supone que la
dirección +y es hacia arriba; te sugiero hacer esto de forma consistente. Lo mismo debes
hacer a la hora de determinar la energía potencial elástica almacenada en un resorte; ten
en cuenta que se mide la elongación con respecto a la longitud natural del resorte.
Lista las energías cinéticas y potenciales iniciales y finales. En general, algunas
serán conocidas y otras no. Usa símbolos algebraicos para las coordenadas o velocidades
desconocidas.
Identifica las fuerzas no gravitatorias que efectúan trabajo. Los diagramas de
cuerpos libres siempre son útiles. Calcula el trabajo Wotras realizado por tales fuerzas. Si
alguna de las cantidades que necesitas son incógnitas, represéntalas con símbolos
algebraicos.
Relaciona las energías cinética y potencial y el trabajo no gravitatorio Wotras usando
la ecuación:
EC1+EP1+Wotras=EC2+EP2
Si Wotras=0, tendremos la ecuación EC1+EP1=EC2+EP2. Despeja la cantidad desconocida.
Ten presente, aquí y más adelante, que el trabajo efectuado por cada fuerza debe
estar representado en EP2-EP1=∆EP o en Wotras, pero nunca en ambos. El trabajo gravitatorio
está incluido en ∆EPg; no lo incluyas otra vez en Wotras.
Estudio energético del movimiento del punto
En la última parte del tema empezaremos
con el estudio energético del movimiento del
punto. En ocasiones sólo estaremos interesados en
comprender cualitativamente algunas de las
características del movimiento de la partícula, y
para ello, nos puede bastar con el análisis de la
curva que representa gráficamente la función de
la energía potencial, EP(x), frente a la coordenada
posicional x de la partícula. Veremos una posible curva de energía potencial, tal como la
representada en la figura, para un movimiento unidimensional. Estudiaremos genéricamente
esta curva, y podrás, operando de igual modo, resolver los problemas planteados en este
tema.
La fuerza que actúa sobre la partícula es
función de la posición de ésta y su módulo y
dE (x)
; pero
sentido vienen dados por F = − P
dx
dEP (x)
es justo la pendiente de la curva EP=EP(x),
dx
que es positiva cuando la curva crece (al aumentar
x) y negativa cuando decrece. Por consiguiente, y teniendo en cuenta el signo negativo que
aparece en la expresión de la fuerza, ésta será negativa (dirigida hacia la izquierda) cuando
la energía potencial crece y será positiva (dirigida hacia la derecha) cuando la energía
potencial decrece. Esta circunstancia se indica en la figura mediante las flechas rojas
horizontales. En los puntos en los que EP(x) presenta un valor máximo o mínimo relativo, es
dEP (x)
decir, en aquellos puntos en los que
= 0 la fuerza será nula; tales posiciones lo
dx
serán de equilibrio.
Aquellas posiciones, como la x0, en las que EP(x) presenta un valor mínimo son
posiciones de equilibrio estable; una partícula en reposo en una de tales posiciones
permanecerá en reposo en ella, y si se desplaza ligeramente de tal posición se verá
sometida a una fuerza recuperadora que tratará de devolverla a la posición de equilibrio,
produciéndose oscilaciones alrededor de dicha
posición. En aquellas otras posiciones, como la x10,
en las que EP(x) adquiere un valor máximo con
respecto a las posiciones vecinas, el equilibrio es
inestable; la partícula podrá permanecer en reposo
en tal posición, pero si se la desplaza ligeramente
de ella, aparecerá una fuerza que tiende a alejarla
aún más de la posición de equilibrio inestable. Por
último, en aquellas regiones en las que EP(x) sea constante el equilibrio será neutro o
indiferente, puesto que no aparecerán fuerzas recuperadoras ni repulsivas al desplazar
ligeramente una partícula que se encuentre en tal región (al ser EP(x) constante será F=0).
Consideremos ahora que la partícula
tiene una energía total E (que permanecerá
constante en el movimiento si sólo actúan
fuerzas conservativas sobre ella) que vendrá
indicada por una línea horizontal en la
representación gráfica de la figura. En cualquier
posición x, la energía potencial EP(x) de la
partícula vendrá dada por la ordenada de la
curva EP=EP(x) y la energía cinética de la partícula será EC=E-EP(x), de modo que vendrá
representada por la distancia de la curva EP(x) (en el punto dado x) a la línea E. Puesto que
la energía cinética es esencialmente positiva (una energía cinética negativa implicaría una
velocidad imaginaria) resulta evidente que para una energía total dada E, la partícula
únicamente podrá encontrarse en aquellos puntos en los que E> EP(x).
Así pues, en la gráfica de la figura, se
advierte inmediatamente que la menor energía
posible es E0; para esta energía la partícula sólo
puede permanecer en reposo en x0.
Con una energía algo mayor, tal como la
E1, la partícula puede moverse entre los puntos
x1 y x2; su velocidad disminuye al acercarse a los
puntos x1 o x2 anulándose en ellos, de modo que
la partícula se detiene e invierte su sentido de
movimiento al alcanzar dichos puntos, llamados
puntos de retorno. Si la energía es aún mayor,
tal como la E2, la partícula podrá oscilar entre
los puntos x3 y x4 o permanecerá en reposo en el
punto x5.
Si la partícula tiene una energía aún
mayor, tal como la E3, existen cuatro puntos de
retorno, de manera que hay dos regiones de
movimiento permitidos. Así, la partícula podrá
oscilar entre x6 y x7 o entre x8 y x9, esto es, en
uno u otro pozo de potencial, pero no podrá pasar de una región a otra porque ello exige
pasar por la región x7 ↔ x8 donde su energía cinética sería negativa (región prohibida).
Decimos que las dos regiones donde el movimiento es posible están separadas por una
barrera de potencial.
En el nivel de energía E4 sólo existe un
punto de retorno; si la partícula está
desplazándose inicialmente hacia la izquierda, al
llegar al punto x11 “rebotará” y se dirigirá hacia
la derecha, acelerándose en los pozos de
potencial y frenándose al pasar sobre las
barreras de potencial. Para energías superiores a
E5 no hay puntos de retorno y la partícula se moverá únicamente en un sentido (el inicial)
acelerándose y frenándose al pasar sobre los pozos y las barreras de potencial
respectivamente, pero sin invertir nunca su sentido de movimiento.
TEMA 3
TRABAJO Y ENERGÍA
PROBLEMAS
1 . - A la esfera A se le comunica una
velocidad descendente v0 y oscila describiendo
una circunferencia vertical de radio L=2 m y
centro O. Hallar: a) la menor velocidad v0
para la que la esfera llegará al punto B al
oscilar alrededor del punto O si AO es una
cuerda; b) la menor velocidad v0 para la que
la esfera llegará al punto B al oscilar
alrededor del punto O si AO es una varilla
delgada de masa despreciable; c) si AO es
una cuerda y la velocidad v0 tiene un módulo
de 5 m/s, hallar el ángulo θ para el que se
rompe la cuerda sabiendo que ésta puede
soportar una tensión máxima igual al doble del peso de la esfera; d) si la cuerda no se
rompiese, decir si podría con esa velocidad inicial trazar el círculo completo, y en caso
contrario, determinar a qué altura dejaría la trayectoria circular.
a) Por supuesto, el punto crítico es el punto superior, B. Puesto que AO
es una cuerda, como fuerza sólo podrá ejercer una tensión, lo cual implica que
en el punto más alto de la trayectoria, si hacemos el diagrama de sólido libre
de la esfera tendremos dos fuerzas, el peso y la tensión, ambas verticales y
hacia abajo. Esto implica que puesto que hay fuerzas en el eje vertical tiene
que haber aceleración en este eje, y dicha aceleración tiene que ser la
componente normal (está en la dirección del radio de curvatura y apuntando
hacia el centro de curvatura). Esta aceleración depende directamente de la
velocidad, de modo que cuanto mayores sean las fuerzas mayor será la
velocidad en el punto B, y eso implica mayor velocidad en el punto A. Si queremos que la
velocidad sea mínima, las fuerzas tienen que ser mínimas; dado que el peso es constante
sólo puede variar la tensión, y el valor mínimo de la tensión es cero. Así pues, la mínima
velocidad v0 en el punto A implica que la tensión en el punto B tiene que ser nula, en cuyo
caso tendremos, aplicando la segunda ley de Newton:
vB2
⇒ vB2 = gL
L
Ahora para determinar la mínima velocidad v0
aplicamos la conservación de la energía, entre la
situación inicial en el punto A y la situación final en B.
Tendremos:
ETA+Wotras=ETB
Tomamos como nivel de energía potencial
gravitatoria el nivel de A. De este modo, en el punto A
sólo tenemos energía cinética puesto que la velocidad es
v0, mientras que en el punto B tenemos energía potencial
gravitatoria y energía cinética, ya que hemos visto que
la velocidad en el punto B es vB. En cuanto al trabajo realizado por otras fuerzas distintas
al peso, sólo aparece la tensión, que en todo momento es perpendicular al desplazamiento
de su punto de aplicación, de modo que no realiza trabajo. Así pues:
ΣFn = manB ⇒ mg + T = manB ⇒ T = 0 ⇒ mg = m
ETA + Wotras = ETB ⇒ ECA = ECB + EPgB ⇒
1
1
1
1
mv 2 = mv 2 + mgL ⇒ v02 = vB2 + gL
2 0 2 B
2
2
1 2 1
1
3
v0 = gL + gL ⇒ v02 = gL ⇒ v0 = 3gL = 3 ⋅ 9.8 ⋅ 2 = 7.67 m / s
2
2
2
2
v0=7.67 m/s
b) Ahora supongamos que AO es una varilla. Como hemos visto anteriormente,
la mínima velocidad v0 implica la mínima velocidad vB. Si AO es una varilla rígida,
puede actuar como apoyo, de modo que en el punto B podríamos tener una fuerza
vertical y hacia abajo, que es el peso, y otra vertical y hacia arriba, que es la normal
proporcionada por el apoyo de la varilla. Estas dos fuerzas pueden ser iguales de tal
modo que el sumatorio de fuerzas es nulo y la aceleración normal en el punto B es
nula, es decir, la velocidad en B es nula.
Aplicamos como antes la conservación de la energía teniendo en cuenta que en
B no tenemos energía cinética y nos queda:
1
1
ETA + Wotras = ETB ⇒ ECA = EPgB ⇒ mv02 = mgL ⇒ v02 = gL ⇒ v0 = 2gL =
2
2
= 2 ⋅ 9.8 ⋅ 2 = 6.26 m / s
v0=6.26 m/s
Newton:
c) Nos centramos ahora
en el caso de la cuerda.
Hacemos el diagrama de sólido
libre en el punto en que la
tensión es máxima, que sería
justo donde se produce la
rotura
(punto
que
denominaremos C). Tomamos
como ejes el normal y el
tangencial
y
tendremos,
aplicando la segunda ley de
vC2
L
Teniendo en cuenta que la tensión máxima que soporta el cable es el doble del peso
de la esfera:
ΣFn=man ⇒ Tmáx − mgsenθ = m
Tmáx − mgsenθ = m
vC2
v2
v2
⇒ 2mg − mgsenθ = m C ⇒ 2g − gsenθ = C
L
L
L
Nos falta solamente la velocidad en ese punto. Para
ello aplicamos la conservación de la energía entre la
posición inicial A y el punto en que la tensión es máxima.
Nos queda:
ETA + Wotras = ETC ⇒ ECA + EPgA = EcC
1
1
1
1
mv 2 + mgh = mvC2 ⇒ v02 + gh = vC2 ⇒ v02 + 2gLsenθ = vC2
2
2
2
2 0
Sustituimos esta expresión en la ecuación que
hemos obtenido para las fuerzas:
vC2
v 2 + 2gLsenθ
⇒ 2g − gsenθ = 0
⇒ 2gL − gLsenθ = v02 + 2gLsenθ
L
L
2gL − v02 2 ⋅ 9.8 ⋅ 2 − 52
2gL − v02 = 3gLsenθ ⇒ senθ =
=
= 0.241 ⇒ θ = 13.97 º
3gL
3 ⋅ 9.8 ⋅ 2
2g − gsenθ =
θ=13.97º
d) Obviamente no se puede trazar el círculo completo, ya que la velocidad mínima
necesaria es de 7.67 m/s y la que nos dan ahora es 5 m/s, inferior a la mínima.
NO SE PUEDE TRAZAR EL CÍRCULO COMPLETO
Ahora vemos en
qué punto se rompe la
trayectoria (punto D).
En el punto en que la
trayectoria deja de ser
circular la tensión deja
de actuar ya que la
cuerda
comienza
a
arrugarse y el cuerpo
se encuentra solo bajo
la acción del peso. En ese punto la esfera se encuentra a una altura h’ por encima de la
posición inicial y el diagrama de sólido libre será el de la figura. Aplicando la segunda ley de
Newton:
2
v2
v2
h' v
ΣFn = manD ⇒ mgsenα = m D ⇒ g = D ⇒ h' = D
L
L
L
g
Sólo nos falta determinar la velocidad de
la esfera en el punto D. Para ello aplicamos de
nuevo la conservación de la energía entre la
posición inicial A y el punto D. Tendremos:
ETA + Wotras = ETD ⇒ ECA = EcD + EPgD
1
1
mv02 = mvD2 + mgh'⇒ v02 = vD2 + 2gh'
2
2
vD2 = v02 − 2gh'
Sustituyéndolo
Newton:
h' =
en
la
segunda
ley
de
vD2
v 2 − 2gh'
v2
52
⇒ h' = 0
⇒ gh' = v02 − 2gh'⇒ h' = 0 =
= 0.85 m
g
g
3g 3 ⋅ 9.8
h’=0.85 m
2. En
la
figura
se
ha
representado una vagoneta de una
montaña rusa. La vagoneta y sus cuatro
ocupantes tienen un peso total de 4500
N. La celeridad de la vagoneta es de 56
km/h cuando pasa por el punto A de la
vía. Tratando la vagoneta con sus
ocupantes
como
punto
material
determinar: a) la velocidad de la vagoneta
en el punto más bajo del rizo; b) la fuerza
que la vía ejerce sobre la vagoneta en el
punto B; c) la fuerza que la vía ejerce
sobre la vagoneta en el punto C; d) la mínima celeridad que ha de llevar la vagoneta
en el punto más alto del rizo para mantenerse en contacto con la vía.
a) En primer lugar pasamos la velocidad al sistema internacional y determinamos la
masa de la vagoneta y sus ocupantes:
P 4500
vA=56 km/h=15.56 m/s; m = =
= 459.48 kg
g
9.8
Llamaremos punto P al punto más bajo de la trayectoria. En él tomaremos el origen
de energías potenciales. Aplicando el teorema de conservación de la energía entre los
puntos A y P y tendremos:
ETA+Wotras=ETP
En el punto A tenemos tanto energía cinética (la velocidad es vA) como potencial
gravitatoria. En cuanto al trabajo, además del peso en este caso actúa sólo sobre el sistema
la fuerza normal, que por ser perpendicular al desplazamiento no realiza trabajo. Y en el
punto más bajo de la trayectoria sólo tenemos energía cinética, ya que la potencial
gravitatoria será nula por convenio. Nos queda entonces:
1
1
1
1
ETA+Wotras=ETP ⇒ ECA+EPgA=ECP ⇒ mvA2 + mghA = mvP2 ⇒ vA2 + ghA = vP2
2
2
2
2
1
1 2
2
15.56 + 9.8 ⋅ 24 = vP ⇒ vP = 26.69 m / s
2
2
vP=26.69 m/s
b) Para determinar la fuerza que la vía
ejerce sobre la vagoneta en el punto B tenemos que
realizar el diagrama de sólido libre del cuerpo en ese
punto. Como fuerzas tendremos el peso (vertical y
hacia abajo) y la normal (perpendicular a la tangente
en ese punto y apuntando hacia el sólido). En cuando
a aceleraciones puesto que el movimiento es circular
aparecerán las dos componentes de aceleración,
normal y tangencial. La normal tiene la dirección del radio de curvatura y apuntando hacia el
centro de curvatura (horizontal y hacia la izquierda) y la tangencial tiene la dirección
tangente a la trayectoria y sentido contrario a la velocidad ya que al subir la velocidad
disminuye (vertical y hacia abajo). Podemos ver en el gráfico que el sentido de fuerzas y
aceleraciones verifica perfectamente la segunda ley de Newton. Aplicando dicha ley:
vB2
r
Nos falta sólo calcular la velocidad de la vagoneta en el punto B. Aplicamos, como
antes, la conservación de la energía entre la posición A y la B. En la B tendremos también
energía potencial y cinética, y tendremos ya en cuenta que la normal no realiza trabajo. Así
pues:
1
1
ETA+Wotras=ETB ⇒ ECA+EPgA=ECB+EPgB ⇒ mvA2 + mghA = mvB2 + mghB
2
2
1 2
1
1
1
vA + ghA = vB2 + ghB ⇒ 15.562 + 9.8 ⋅ 24 = vB2 + 9.8 ⋅ 12 ⇒ vB2 = 477.175 m2 / s2
2
2
2
2
Y sustituyendo, la reacción de la vía es:
ΣFn=man ⇒ NB = manB = m
vB2
477.175
= 459.48
= 18271.04 N
r
12
NB=18271.04 N
c) Vamos a hacer lo mismo en el punto C. Las fuerzas serán las mismas, sólo que al
ser la normal perpendicular a la tangente, en el punto C la normal será vertical y hacia
abajo. Así pues, al no existir fuerzas en dirección tangencial en ese punto la aceleración
tangencial tiene que ser nula. Esto es lógico, ya que el punto más alto de la trayectoria es el
punto en que la energía potencial es máxima y por tanto la cinética es mínima. Esto implica
NB = m
que la velocidad en el punto C es mínima y la condición de
mínimo es que su derivada sea nula. Puesto que por
definición la aceleración tangencial es la derivada del
módulo de la velocidad respecto del tiempo, en dicho punto
esta derivada es nula. Tendremos lo que aparece en la
figura, y aplicando de nuevo la segunda ley de Newton:
ΣFn=man ⇒ NC+mg=manC
 v2

NC = manC − mg = m(anC − g ) = m C − g 
 r



Igual que antes nos falta sólo la velocidad en el punto C. Operamos de igual modo:
1
1
ETA+Wotras=ETC ⇒ ECA+EPgA=ECC+EPgC ⇒ mvA2 + mghA = mvC2 + mghC
2
2
1 2
1 2
1
1 2
2
vA + ghA = vC + ghC ⇒ 15.56 + 9.8 ⋅ 24 = vC + 9.8 ⋅ 24 ⇒ vC2 = 241.975 m2 / s2
2
2
2
2
Lógicamente la velocidad en el punto C es la misma que la velocidad en el punto A, ya
que los dos se encuentran a la misma altura. Sustituyendo, la reacción de la vía en el punto
C es:

 v2

 241.975
NC = m C − g  = 459.48
− 9.8  = 4762.33 N
 r

12




NC=4763.3 N
d) El contacto con la vía lo establece la reacción
normal. Cuanto menor es la normal menor es el contacto
con la vía, y justamente cuando la normal se anula es
cuando se pierde el contacto. Por ello, la mínima
celeridad en el punto C que justo anula el contacto será
cuando la normal valga cero. Tendremos lo que aparece
en la figura y aplicando la segunda ley de Newton:
ΣFn=man ⇒ mg=manCmín ⇒ g =
2
vCmín
r
⇒ vCmín = gr = 9.8 ⋅ 12 = 10.84 m / s
vCmín=10.84 m/s
3. - Una bola de 680 g que puede deslizar sobre una
superficie horizontal lisa está unida a un punto fijo O mediante
un cordón elástico de constante k=1 46 N/m y longitud natural
580 mm. La bola se coloca en el punto A, a 763 mm de O y se le
comunica una velocidad inicial v0 perpendicular a OA. Hallar: a) el
mínimo valor permitido de la celeridad v0 para que el cordón no se
afloje; b) la distancia más corta “d” de la bola al punto O si la
misma recibe una celeridad inicial igual a la mitad de la calculada
en la parte a); c) cuál sería en este caso la celeridad máxima.
a) Si el cordón no se afloja quiere decir que en el punto más
próximo al punto fijo O la distancia d debe ser de 580 mm=0.58 m. Tomamos entonces dos
puntos, el punto A, inicio del movimiento, y el punto B, que será el punto en que la distancia
es mínima. En este último punto la curvatura debe cambiar puesto que a partir de ahí la
distancia a O comenzará a aumentar. En este punto B por tanto la velocidad tiene que ser
perpendicular al radio vector.
Se trata además de un caso de fuerzas
centrales, ya que en el plano del movimiento sólo aparece
la fuerza de recuperación elástica, que siempre va a
pasar por el punto O. Cuando se trata de fuerzas
centrales hay dos parámetros que se conservan, uno
escalar, la energía, y otro vectorial, el momento angular.
Aplicamos por tanto la conservación de estos dos
parámetros entre las posiciones A y B. Tendremos para
la energía:
ETA = ETB ⇒ ECA + EPeA = ECB
1
1
1
mv02 + k∆lA2 = mv 2 ⇒ mv02 + k∆lA2 = mv 2
2
2
2
0.68v02 + 146 ⋅ 0.1832 = 0.68v 2
Y para el momento angular:
LA = LB ⇒ rA × mv 0 = rB × mv ⇒ rAv0 senϕA = rB vsenϕB
0.763v0sen90º=0.580vsen90º ⇒ 0.763v0=0.580v
Tenemos un sistema de dos ecuaciones y dos incógnitas:
0.68v02 + 146 ⋅ 0.1832 = 0.68v 2
0.763v0=0.580v
De la segunda expresión:
0.763v0=0.580v ⇒ v=1.3155v0
Y sustituyendo en la primera:
0.68v02 + 146 ⋅ 0.1832 = 0.68v 2 ⇒ 0.68v02 + 4.889 = 0.68(1.3155v0 )2 ⇒ v0 = 3.137 m / s
v0=3.137 m/s
b) Si la bola recibe una velocidad igual a la mitad de la
v
3.137


calculada anteriormente  vA = 0 =
= 1.569 m / s  el cordón
2
2


sí se aflojará, luego la distancia mínima será inferior a 0.580 m y
la denominaremos d. Lo que sí seguirá ocurriendo es que en este
punto de mínima distancia que llamaremos C la curvatura de la
trayectoria cambia y la velocidad es perpendicular al radio
vector. Se seguirán conservando la energía total y el momento
lineal luego tendremos para la energía total:
ETA = ETC ⇒ ECA + EPeA = ECC
1
1
1
mvA2 + k∆lA2 = mvC2 ⇒ mvA2 + k∆lA2 = mvC2
2
2
2
0.68 ⋅ 1.5692 + 146 ⋅ 0.1832 = 0.68vC2 ⇒ vC = 3.11 m / s
Y para el momento angular:
LA = LC ⇒ rA × mvA = rC × mv C ⇒ rAvAsenϕA = rC vC senϕC
0.763 · 1.569sen90º=3.11dsen90º ⇒ d=0.385 m
d=0.385 m
c) La velocidad máxima será en el punto en que la distancia es mínima, es decir, en el
punto C:
vmáx=vC=3.11 m/s
vmáx=3.11 m/s
4. - Una piedra de 1 5 kg baja deslizándose una
colina nevada, partiendo del punto A con una rapidez de
1 0 m/s. No hay fricción en la colina entre los puntos A y
B, pero sí en el terreno plano en la base, entre B y la
pared. Después de entrar en la región áspera, la piedra
recorre 1 00 m y choca con un resorte muy largo y ligero
cuya constante de fuerza es de 2 N/m. Los coeficientes
de fricción cinética y estática entre la piedra y el suelo horizontal son de 0. 20 y
0. 80 respectivamente. a) ¿Qué rapidez tiene la piedra al llegar al punto B? b) ¿Qué
distancia comprimirá la piedra el resorte? c) ¿La piedra se moverá otra vez después
de haber sido detenida por el resorte?
a) En primer lugar aplicamos la conservación de la energía entre la posición A y la
posición B. Tomaremos como nivel de energía potencial gravitatoria nula la del suelo
horizontal. Así, tendremos:
ETA+Wotras=ETB
En la posición A tenemos energía potencial gravitatoria y energía cinética mientras
que en B tendremos sólo energía cinética. En cuanto al trabajo, aparte del peso sólo
aparece la normal, que por ser perpendicular al desplazamiento no realiza trabajo. Nos
queda entonces:
1
1
ETA+Wotras=ETB ⇒ ECA+EPgA=ECB ⇒ mvA2 + mghA = mvB2 ⇒ vA2 + 2ghA = vB2
2
2
vB = vA2 + 2ghA = 102 + 2 ⋅ 9.8 ⋅ 20 = 22.18 m / s
vB=22.18 m/s
b) Ahora aplicamos la conservación de la energía entre la situación inicial (A) y la
posición en que el resorte tiene la máxima compresión (posición C).
ETA+Wotras=ETC
En la posición C tendremos solamente energía potencial elástica,
ya que la potencial gravitatoria es nula por convenio y la cinética
es nula también porque en el punto de máxima compresión la
piedra se detiene instantáneamente. En cuanto al trabajo, al
entrar en la zona rugosa además del peso y la fuerza de
recuperación elástica (cuando exista) actúan también la normal
y la fuerza de rozamiento. La normal no realiza trabajo por ser
perpendicular al desplazamiento, pero la fuerza de rozamiento
sí realiza trabajo. Dicha fuerza podemos determinarla aplicando
la segunda ley de Newton:
ΣFY=maY ⇒ N-mg=0 ⇒ N=mg
Puesto que la piedra desliza la fuerza de rozamiento adquiere su valor máximo:
Fr=(Fr)máx=µcN=µcmg
Ahora aplicamos el teorema de conservación de la energía:
1
1
ETA+Wotras=ETC ⇒ ECA+EPgA+WFr=EPeC ⇒ mvA2 + mghA + Fr ⋅ x = k∆xC2
2
2
1
1
1
1
mvA2 + mghA + Fr x cos θ = k∆xC2 ⇒ mvA2 + mghA + µ cmgx cos 180 º = k∆xC2
2
2
2
2
1
1
2
2
2
15 ⋅ 10 + 15 ⋅ 9.8 ⋅ 20 − 0.20 ⋅ 15 ⋅ 9.8(100 + ∆xC ) = 2∆xC ⇒ ∆xC + 29.4∆xC − 750 = 0
2
2
∆xC =
− 29.4 ± 29.42 + 4 ⋅ 750 − 45.78 m
=
2
 16.38 m
Obviamente sólo consideramos la respuesta positiva:
∆xC=16.38 m
c) Hacemos el diagrama de sólido libre del bloque en el
punto C. La piedra se moverá si la fuerza de rozamiento es
superior a la máxima, y no lo hará si la fuerza de rozamiento es
inferior a la máxima. Supongamos que no se mueve. En ese caso
tendremos lo que aparece en la figura, y aplicando la segunda
ley de Newton:
ΣFX=maX ⇒ Fr-k∆xC=0 ⇒ Fr=k∆xC=2 · 16.38=32.76 N
Y la fuerza de rozamiento máxima:
(Fr)máx=µeN=µemg=0.80 · 15 · 9.8=117.6 N
Vemos que la fuerza de rozamiento es inferior a la máxima:
Fr<(Fr)máx ⇒ 32.76<117.6
Por tanto después de detenerse la piedra no se moverá.
NO SE MOVERÁ
5. - Se aplica una fuerza constante de 1 50 N al
collarín B. Si el sistema parte del reposo y la fuerza actúa
durante todo el movimiento, determínese: a) la velocidad del
collarín B al chocar contra el soporte C; b) la tensión en la
cuerda; c) ¿después de qué distancia d se deberá eliminar la
fuerza de 1 50 N si el collarín debe llegar al soporte C con
velocidad cero? No existe rozamiento entre el collarín y la
barra y las poleas se consideran de masa despreciable.
expresar como:
a) En primer lugar vamos a determinar la
relación entre velocidades y aceleraciones de los dos
bloques. Puesto que el collarín viene marcado como B, al
bloque le representaremos con el subíndice A.
Denominamos x e y a las posiciones absolutas del
collarín y el bloque respectivamente con lo cual
tendremos que puesto que los movimientos son
rectilíneos:
dv
dy
dv
dx
= −vA ;
= vB ; A = aA ; B = aB
dt
dt
dt
dt
La longitud de la cuerda que los une la podemos
L=cte=2x+y+ctes
Puesto que la longitud de la cuerda es constante, su derivada tiene que ser cero:
dL
dx dy
=0⇒2
+
= 0 ⇒ 2vB − vA = 0 ⇒ vA = 2vB
dt
dt dt
Y volviendo a derivar respecto del tiempo:
dv
dv
vA = 2vB ⇒ A = 2 B ⇒ aA = 2aB
dt
dt
Ahora
vamos
a
aplicar la conservación de
la energía. Aplicamos la
conservación de la energía
al sistema de dos bloque
más la cuerda que los une,
que no implica nada ya que
por no tener masa no da
lugar nunca a energía. De
este modo, no nos aparecen
las tensiones y no tenemos
que determinar el trabajo que realizan. Como nivel nulo de energía potencial gravitatoria
tomamos la posición más baja del sistema. Es obvio que si el collarín se desplaza 0.6 m hacia
la izquierda, el bloque A tiene que ascender justamente el doble, es decir, 1.2 m. Así pues
tendremos:
ET1+Wotras=ET2
Inicialmente tenemos que la energía cinética es nula
porque el sistema parte del reposo, y en cuanto a energía
potencial gravitatoria tendría el collarín C que está a una altura
hB respecto de la posición más baja. En la situación final los dos
bloques tienen energía cinética y los dos bloques tienen energía
potencial gravitatoria. Respecto al trabajo, para el sistema total
además de los pesos tenemos que aparecen la reacción de la
barra y la fuerza F de 150 N. La reacción de la barra no realiza
trabajo porque es perpendicular al desplazamiento, pero la
fuerza F sí realiza trabajo. Por supuesto, habría reacciones en la
polea y en el anclaje de la pared, pero no las tengo en cuenta
porque puesto que no se desplazan tampoco realizan trabajo. Sólo
realiza trabajo de todas las fuerzas la de 150 N. Nos queda
entonces:
ET1+Wotras=ET2 ⇒ EPgB1+WF=ECA2+ECB2+EPgA2+EPgB2
1
1
1
1
mB ghB + F ⋅ xC = mAvA2 + mB vB2 + mAghA + mB ghB ⇒ FxC cos 0º = mAvA2 + mB vB2 + mAghA
2
2
2
2
Tenemos en cuenta la relación entre las velocidades:
1
1
vA = 2vB ⇒ 150 ⋅ 0.6 = 3(2vB )2 + 8vB2 + 3 ⋅ 9.8 ⋅ 1.2 ⇒ 54.72 = 10vB2 ⇒ vB = 2.34 m / s
2
2
vB=2.34 m/s
b) Para determinar la tensión en la cuerda tenemos que hacer los
diagramas de sólido libre de los dos bloques y aplicar la segunda ley de
Newton. Para el bloque A tendremos:
ΣFY=mAaAY ⇒ T-mAg=mAaA ⇒ T-3 · 9.8=3aA ⇒ T-29.4=3aA
Ahora para el collarín B hacemos lo mismo:
ΣFX=mBaBX ⇒ F-2T=mBaB ⇒ 150-2T=8aB
Y por último tenemos la ecuación que nos liga las dos
aceleraciones:
aA=2aB
Tenemos un sistema de tres ecuaciones y tres
incógnitas:
T-29.4=3aA
150-2T=8aB
aA=2aB
Sustituimos la última expresión en las dos anteriores:
T-29.4=3 · 2aB ⇒ T-29.4=6aB
150-2T=8aB
De la segunda ecuación:
150-2T=8aB ⇒ aB=18.75-0.25T
Y sustituyendo en la primera:
T-29.4=6aB ⇒ T-29.4=6(18.75-0.25T) ⇒ T-29.4=112.5-1.5T ⇒ T=56.76 N
T=56.76 N
c) Volvemos a aplicar la conservación de la energía entre la situación inicial y la
final, teniendo en cuenta ahora que la fuerza F sólo actúa durante un espacio d y que la
velocidad final de los dos bloques es nula, de modo que al final no tenemos energía cinética
para ninguno de los dos bloques. El resto nos quedaría igual, de modo que tendremos:
ET1+Wotras=ET2 ⇒ EPgB1+WF=EPgA2+EPgB2
mB ghB + F ⋅ d = mAghA + mB ghB ⇒ Fd cos 0º = mAghA ⇒ 150d = 3 ⋅ 9.8 ⋅ 1.2 ⇒ d = 0.2352 m
d=0.2352 m
6. - En un juego de
habilidad,
los
jugadores
hacen
que
se
deslicen
monedas por una superficie
de madera, según se indica
en la figura. Para ganar, la
moneda ha de detenerse
entre las líneas C y D de la
superficie
inferior.
El
coeficiente de rozamiento entre las monedas de 5 g y el suelo vale 0. 2, las aristas
son bruscas pero lisas y el punto desde el cual el jugador ha de soltar la moneda se
halla a 1 m de la arista B. Determinar el campo de velocidades iniciales
correspondientes a tiros ganadores.
El rango de velocidades que determina los tiros
ganadores viene definido por los extremos C y D de las
líneas. Comencemos por la menor de las velocidades que da
lugar a un tiro ganador, que es aquella que hace que la
moneda llegue justamente al punto C. Si empezamos desde
el final del juego, a partir de B tenemos un tiro parabólico horizontal, cuya velocidad inicial
denominaremos vB. El ángulo del plano inclinado será:
5
tgα =
⇒ α = 22.62º
12
Dicho plano inclinado tiene una altura de 100 mm=0.1 m y una longitud horizontal de:
100
100
100
tgα =
=
= 240 mm = 0.24 m
⇒x=
x
tgα tg22.62º
Por tanto en el tiro parabólico la altura recorrida será de 0.1 m y el alcance será de
0.24+0.3=0.54 m. Si nos centramos en el eje vertical el movimiento es rectilíneo
uniformemente acelerado, siendo la aceleración la de la gravedad. Así pues:
1 2
1
gt ⇒ 0 = 0.1 − 9.8t2 ⇒ t = 0.143 s
2
2
Y en el eje X el movimiento es rectilíneo y uniforme (velocidad constante):
x
0.54
vB = máx =
= 3.78 m / s
t
0.143
Por tanto la moneda tiene que llegar al
punto B con una velocidad de 3.78 m/s. Ahora
aplicamos la conservación de la energía entre la
situación inicial A y la final al llegar a B. Tomamos
como nivel de energía potencial gravitatoria nula la
altura del plano horizontal:
ETA+Wotras=ETB
Tanto en la posición A como en la B sólo tenemos
energía cinética, ya que la potencial gravitatoria es nula por
convenio. En cuanto a las fuerzas, a mayores del peso
actúan sobre la moneda la normal y la fuerza de
rozamiento. La normal no realiza trabajo porque es perpendicular al desplazamiento, pero la
fuerza de rozamiento sí realiza trabajo. Podemos determinar esta fuerza realizando el
diagrama de sólido libre de la moneda y aplicando la segunda ley de Newton, con lo que
tendremos:
ΣFY=maY ⇒ N-mg=0 ⇒ N=mg
Y como la moneda desliza la fuerza de rozamiento adquiere su valor máximo:
Fr=(Fr)máx=µN=µmg=0.5 · 9.8m=1.96m N
Aplicando la conservación de la energía:
1
1
1
1
ETA+Wotras=ETB ⇒ ECA+WFr=ECB ⇒ mv02 + Fr ⋅ x = mvB2 ⇒ mv02 + Fr x cos 180 º = mvB2
2
2
2
2
1
1
1
1
mv02 − 1.96mx = mvB2 ⇒ v02 − 1.96 ⋅ 1 = 3.782 ⇒ v0 = 4.27 m / s
2
2
2
2
Ahora si queremos la velocidad máxima de los tiros ganadores actuaremos igual,
pero el alcance horizontal del tiro parabólico tiene que ser de 0.24+0.3+0.1=0.64 m.
Hacemos todo exactamente igual. Determinamos la velocidad en B:
x
0.64
= 4.48 m / s
vB = máx =
t
0.143
Por tanto la moneda tiene que llegar al punto B con una velocidad de 4.48 m/s.
Llegaremos a la misma ecuación final:
1
1
1
1
mv02 − 1.96mx = mvB2 ⇒ v02 − 1.96 ⋅ 1 = 4.482 ⇒ v0 = 4.90 m / s
2
2
2
2
Por tanto el rango de velocidades es:
4.27 m/s≤v0≤4.90 m/s
yC = yB + vBY t −
7. - Una pequeña esfera B de masa m=1 kg se
suelta desde el reposo en la posición indicada y oscila
libremente en un plano vertical, primero en torno a O
y luego en torno a la espiga A cuando el hilo entra en
contacto con la misma. Hallar la tensión en el hilo: a)
justo antes de que el mismo entre en contacto con la
espiga; b) justo después de entrar en contacto con la
espiga.
a) Vamos a ver con qué velocidad llega la esfera a la espiga. Para ello aplicamos la
conservación de la energía entre la posición inicial B y
la final que llamaremos A y que es inmediatamente
antes de tocar la espiga. Tendremos:
ETB+Wotras=ETA
Tomamos como nivel de energía potencial
gravitatoria la posición más baja de la esfera. Por
tanto inicialmente sólo tenemos energía potencial
gravitatoria, ya que el sistema parte del reposo, y en
la situación final sólo tenemos energía cinética, ya que
por convenio la potencial gravitatoria es nula. En cuanto a las fuerzas, aparte del peso sólo
existe la tensión, que en todo momento es perpendicular al desplazamiento, de modo que no
realiza trabajo. Tendremos entonces:
1
ETB+Wotras=ETA ⇒ EPgB=ECA ⇒ mgh = mvA2 ⇒ vA2 = 2gh = 2 ⋅ 9.8 ⋅ 0.8sen30º = 7.84 m2 / s2
2
Para determinar la tensión hacemos el
diagrama de sólido libre de la esfera en esa posición.
Tendremos como fuerzas el peso y la tensión, y como
aceleraciones puesto que es un movimiento circular
la aceleración normal y la tangencial. Aplicando la
segunda ley de Newton:
ΣFn=man ⇒ T-mgsen30º=man ⇒ T=mgsen30º+man=

v2  
7.84 
= m gsen30º + A  = 1 9.8sen30º +
 = 14.7 N
L
0.8 
 

T=14.7 N
b) Justo después de tocar la espiga la posición es prácticamente la misma, la
velocidad es la misma y la única diferencia está en la aceleración normal, ya que el radio de
curvatura ya no es de 0.8 m sino de 0.4 m. Tendremos entonces que todo es igual salvo la
última expresión, donde tendremos:

v2  
7.84 
T' = m gsen30º + A  = 1 9.8sen30º +
 = 24.5 N
L
'
0.4 
 

T’=24.5 N
8. - Un bloque de masa m=5 kg está unido a
un muelle no deformado de constante k=1 kN/m.
Los coeficientes de rozamiento estático y cinético
entre el bloque y el plano son µs=0. 6 y µk= 0. 5
respectivamente. Si se le aplica al bloque
lentamente una fuerza F hasta que la tensión en el
muelle llega a 1 50 N y entonces se retira repentinamente, hallar: a) la velocidad que
tiene el bloque al volver a la posición inicial (antes de empezar a aplicar la fuerza F);
b) la velocidad máxima que alcanza el bloque; c) la distancia hacia la izquierda que
recorre el bloque hasta detenerse; d) ¿retrocederá después el bloque hacia la
derecha? Si la respuesta es afirmativa, ¿qué distancia recorrerá hasta detenerse?
a) A lo largo del problema tomaremos como nivel de energía potencial gravitatoria
nula el plano del movimiento. Así, puesto que no hay variación de altura, la energía potencial
gravitatoria será siempre nula.
En primer lugar vamos a ver cuál es la elongación del resorte (k=1 kN/m=1000 N/m).
Si la fuerza en el muelle es de 150 N tendremos:
F
150
= 0.15 m
F1 = k∆x1 ⇒ ∆x1 = 1 =
k 1000
Inicialmente el resorte está estirado 0.15 m. En esta situación el bloque parte del
reposo (energía cinética nula). Aplicamos la conservación de la energía entre esta situación
inicial (1) y la que llamaremos (2), que es cuando el bloque pasa de por la posición en la que
el muelle estaba sin deformar. Tendremos pues:
ET1+Wotras=ET2
Para determinar el trabajo, vamos a ver qué fuerzas actúan sobre
el bloque. Hacemos el diagrama de sólido libre, y vemos que aparte del
peso y la reacción del resorte, sobre el bloque actúan la normal y la fuerza
de rozamiento. La normal no realiza trabajo porque en todo momento es
perpendicular al desplazamiento, luego sólo realiza trabajo la fuerza de
rozamiento, que valdrá:
Fr=µkN
Como en la dirección vertical no hay movimiento:
ΣFY=0 ⇒ N-mg=0 ⇒ N=mg ⇒ Fr=µkN=µkmg=0.5 · 5 · 9.8=24.5 N
Sustituyendo en la expresión de la conservación de la energía:
1
1
ET1 + Wotras = ET 2 ⇒ EPe1 + WFr = EC2 + EPe2 ⇒ k∆x12 + Fr ⋅ x = mv22
2
2
En la situación (2) el resorte está sin deformar luego no tenemos energía potencial
elástica:
1
1
1
1
1
1
k∆x12 + Fr ⋅ x = mv22 ⇒ k∆x12 + Fr x cos 180º = mv22 ⇒ k∆x12 − Fr x = mv22
2
2
2
2
2
2
1
1
1000 ⋅ 0.152 − 24.5 ⋅ 0.15 = 5v22 ⇒ v2 = 1.74 m / s
2
2
v2=1.74 m/s
b) Puesto que el movimiento es rectilíneo, si la velocidad del bloque es máxima, su
aceleración tiene que ser nula, luego en esa posición, que llamaremos (3), del diagrama de
sólido libre tendremos:
F
24.5
ΣFx=0 ⇒ k∆x3-Fr=0 ⇒ ∆x3 = r =
= 0.0245 m
k 1000
Aplicamos ahora la conservación de la energía mecánica entre la
situación (1) y la (3):
ET1 + Wotras = ET 3 ⇒ EPe1 + WFr = EC3 + EPe3
1
1
1
2
k∆x12 + Fr ⋅ x = mvmáx
+ k∆x32
2
2
2
1
1
1
2
k∆x12 + Fr x cos 180º = mvmáx
+ k∆x32
2
2
2
1
1 2
1
2
1000 ⋅ 0.15 − 24.5(0.15 − 0.0245) = 5vmáx + 1000 ⋅ 0.02452 ⇒ vmáx = 1.77 m / s
2
2
2
vmáx=1.77 m/s
c) Llamaremos (4) a la posición en la cual el bloque se detiene. En dicha posición por
tanto la energía cinética será nula. Aplicamos de nuevo la conservación de la energía
mecánica entre la situación (1) y la (4):
1
1
ET1 + Wotras = ET 4 ⇒ EPe1 + WFr = EPe 4 ⇒ k∆x12 + Fr ⋅ x = k∆x42
2
2
1
1
1
1
k∆x12 + Fr x cos 180º = k∆x42 ⇒ 1000 ⋅ 0.152 − 24.5(0.15 + ∆x4 ) = 1000∆x42
2
2
2
2
− 24.5 ± 24.52 + 4 ⋅ 500 ⋅ 7.545  0.101 m
=
2 ⋅ 500
negativa
Por tanto el desplazamiento del bloque será:
x=∆x1+∆x4=0.15+0.101=0.251 m
x=0.251 m
d) Una vez detenido el bloque, puede quedarse parado si la fuerza de rozamiento
estática es suficientemente grande como para compensar la fuerza de recuperación
elástica del resorte. Veamos si esto es posible. La máxima fuerza de rozamiento estática
que podemos tener es:
(Fr)smáx=µsN=µsmg=0.6 · 5 · 9.8=29.4 N
La fuerza de recuperación elástica del resorte cuando el bloque se detiene es:
F4=k∆x4=1000 · 0.101=101 N
Vemos pues que la fuerza de rozamiento no puede compensar este valor, luego el
bloque comienza a desplazarse de nuevo hacia la derecha.
SÍ RETROCEDE HACIA LA DERECHA
Denominaremos (5) a la nueva posición en que el bloque se detiene (energía cinética
por tanto nula). Si volvemos a aplicar la conservación de la energía entre las posiciones 4 y
5:
1
1
ET 4 + Wotras = ET 5 ⇒ EPe 4 + WFr = EPe5 ⇒ k∆x42 + Fr ⋅ x = k∆x52
2
2
1
1
1
1
k∆x42 + Fr x cos 180º = k∆x52 ⇒ 1000 ⋅ 0.1012 − 24.5(0.101 + ∆x5 ) = 1000∆x52
2
2
2
2
500∆x32 + 24.5∆x4 − 7.575 = 0 ⇒ ∆x4 =
− 24.5 ± 24.52 + 4 ⋅ 500 ⋅ 2.626  0.052 m
=
2 ⋅ 500
negativo
Por tanto la distancia que recorre hasta detenerse es:
x=∆x4+∆x5=0.101+0.052=0.153 m
x=0.153 m
500 ∆x52 + 24.5∆x5 − 2.626 = 0 ⇒ ∆x5 =
9. - Un pequeño bloque desliza con celeridad
v=2. 4 m/s por una superficie horizontal a una altura
h=0. 9 m sobre el suelo. Hallar: a) el ángulo θ de
despegue de la superficie cilíndrica BCD; b) la distancia
x a la que choca con el suelo. Se desprecian el
rozamiento y la resistencia con el aire.
a) En primer lugar aplicamos la conservación de la
energía entre la posición del bloque en el punto B y la
posición del bloque en el punto C.
ETB+Wotras=ETC
Tomamos el punto C como nivel de energía potencial
gravitatoria. Por tanto, en el punto B tenemos energía
cinética, ya que el bloque lleva una velocidad de 2.4 m/s, y energía potencial gravitatoria, ya
que también tiene altura. En cuanto al trabajo, a mayores del peso sólo actúa la normal, que
es perpendicular al desplazamiento y por tanto no realiza trabajo. Y por último, en la
posición C el bloque no tiene energía potencial gravitatoria por convenio y sí que tiene
cinética. Nos queda entonces:
1
1
1
1
ETB+Wotras=ETC ⇒ ECB+EPgB=ECC ⇒ mvB2 + mghB = mvC2 ⇒ vB2 + ghB = vC2
2
2
2
2
1 2
1
vB + g(h − h cos θ) = vC2
2
2
Tenemos dos incógnitas, el ángulo θ y la
velocidad del cuerpo en el punto C. Para
determinar esta velocidad hacemos el diagrama
de sólido libre del bloque en el punto C. El bloque
está sometido a su propio peso y a la normal, pero
puesto que en el punto C el bloque despega, se
pierde el contacto y por tanto la normal se hace
cero. En cuanto a aceleraciones, como el bloque desliza por un arco de circunferencia
tendrá dos componentes de aceleración, tangencial y normal. Aplicando la segunda ley de
Newton tendremos:
ΣFn = man ⇒ mg cos θ = m
vC2
⇒ vC2 = grC cos θ = gh cos θ
rC
Sustituyendo en la ecuación de la energía:
1 2
1
1
1
1
1
v + g(h − h cos θ) = vC2 ⇒ vB2 + g(h − h cos θ) = gh cos θ ⇒ vB2 + gh − gh cos θ = gh cos θ
2 B
2
2
2
2
2
1 2
vB + gh
1 2
1
1 2
3
2
vB + gh = gh cos θ + gh cos θ ⇒ vB + gh = gh cos θ ⇒ cos θ =
=
3
2
2
2
2
gh
2
1
2.42 + 9.8 ⋅ 0.9
2
=
= 0.884 ⇒ θ = 27.83º
3
9.8 ⋅ 0.9
2
θ=27.83º
b) A continuación, y desde el punto C, tenemos un tiro parabólico, ya que el bloque
queda sometido exclusivamente a la acción de la gravedad. La velocidad inicial de este tiro
parabólico es la del punto C:
vC= gh cos θ = 9.8 ⋅ 0.9 cos 27.83º = 2.793 m / s
Tendremos entonces lo que aparece en la figura. Si nos
centramos ahora en el eje Y sabemos que el bloque llega al suelo en el
punto E. En el eje Y el movimiento es rectilíneo uniformemente
acelerado, siendo la aceleración la de la gravedad. Así pues:
1
1
yE = yC − vCy t − gt2 ⇒ yE = h cos θ − vC senθt − gt2
2
2
1
0 = 0.9 cos 27.83º −2.793sen27.83º t − 9.8t2 ⇒ 4.9t2 + 1.304t − 0.796 = 0
2
− 1.304 ± 1.3042 + 4 ⋅ 4.9 ⋅ 0.796  0.291 s
=
2 ⋅ 4.9
− 0.558 s
Obviamente un tiempo negativo no tiene sentido físico, luego el bloque tarda 0.291 s
en ir desde el punto C hasta el punto D.
Ahora pasamos al eje X, en el cual el movimiento es rectilíneo y uniforme, de modo
que para el eje X tendremos:
xE=x0+vCxt=vCcosθt=2.793cos27.83º · 0.291=0.719 m
Y el parámetro x que nos pide el problema será:
t=
x=xC+xE=hsenθ+xE=0.9sen27.83º+0.719=1.14 m
x=1.14 m
1 0. - La corredera de 3 kg se abandona
partiendo del reposo en el punto A y desliza con
rozamiento despreciable en un plano vertical a lo
largo de la guía circular. El resorte al que está
unida tiene una constante de 400 N/m y su longitud
sin deformar es de 60 cm. Determinar: a)
aceleración de la corredera y reacción de la barra
en el punto A; b) velocidad de la corredera al
pasar por el punto B; c) aceleración de la
corredera y reacción de la barra en el punto B inmediatamente antes de pasar al
tramo horizontal; d) aceleración de la corredera y reacción de la barra en el punto B
inmediatamente después de pasar al tramo horizontal.
a) Hacemos el diagrama de sólido libre de la
corredera en el punto A. En cuanto a fuerzas tendremos
el peso (vertical y hacia abajo), la reacción del resorte
(está estirado luego será horizontal y hacia la derecha)
y la normal que ejerce la barra (horizontal y hacia la
derecha). En cuanto a aceleraciones, como está trazando
un arco de circunferencia habría en principio dos
componentes, normal y tangencial, pero la normal en esta
posición es nula porque parte del reposo, luego sólo
tenemos la componente tangencial que será vertical y hacia abajo. Aplicamos ahora la
segunda ley de Newton:
ΣFn=manA ⇒ kxA-NA=0 ⇒ NA=kxA=k(lA-l0)=400(1.2-0.6)=240 N
NA=240 N
ΣFt=mat ⇒ mg=maA ⇒ aA=g=9.8 m/s2
aA=9.8 m/s2
b) Ahora aplicamos el teorema de
conservación de la energía entre la posición
A, en que la corredera parte del reposo, y la
posición B, por donde pasa con velocidad vB.
ETA+Wotras=ETB
Tomamos como nivel de energía
potencial gravitatoria nula la posición más
baja, es decir, la de B. En A por tanto
tenemos energía potencial gravitatoria y
energía potencial elástica, siendo el
alargamiento del muelle:
xA=lA-l0=1.2-0.6=0.6 m
En cuanto al trabajo, aparte del peso y la fuerza de recuperación elástica sólo
actúa la normal, que en todo momento es perpendicular al desplazamiento y no realiza
trabajo. Y en la posición B la corredera tiene energía cinética y energía potencial elástica,
ya que el alargamiento del resorte en esta situación es:
xB = lB − l0 = 0.62 + 0.62 − 0.6 = 0.2485 m
Por tanto, aplicando el teorema de conservación de la energía:
1
1
1
ETA+Wotras=ETB ⇒ EPgA+EPeA=EPeB+ECB ⇒ mghA + kxA2 = kxB2 + mvB2
2
2
2
1
1
1 2
2
2
3 ⋅ 9.8 ⋅ 0.6 + 400 ⋅ 0.6 = 400 ⋅ 0.2485 + 3vB ⇒ vB = 7.178 m / s
2
2
2
vB=7.178 m/s
c) Inmediatamente antes de entrar en el tramo horizontal la velocidad de la
corredera es vB y se encuentra en el último punto de una trayectoria curva. Por tanto,
tendrá dos componentes de aceleración, una tangencial (tangente a la trayectoria) y una
normal (en la dirección del radio de curvatura y apuntando hacia el centro de curvatura).
Esta última componente es conocida, vale:
vB2 7.1782
=
= 85.873 m / s2
r
0.6
En cuanto a fuerzas aplicadas sobre la
corredera, tendremos el peso, vertical y hacia
abajo, la reacción del resorte, que como es de
tensión irá hacia fuera de la corredera y que
formará un ángulo de 45º con la vertical, y la
normal de la guía, que será vertical y hacia
arriba. Al trazar el diagrama de sólido libre
de la corredera tendremos pues lo que
aparece en la figura. Aplicamos la segunda ley de Newton:
ΣFn=man ⇒ NB+kxBsen45º-mg=manB ⇒ NB=manB-kxBsen45º+mg=
=3 · 85.873-400 · 0.2485sen45º+3 · 9.8=216.733 N
NB=216.733 N
kx cos 45º 400 ⋅ 0.2485 cos 45º
ΣFt=mat ⇒ kxBcos45º=matB ⇒ atB = B
=
= 23.429 m / s2
m
3
La aceleración tiene dos componentes, normal y tangencial, luego su módulo será:
anB =
aB = an2 + at2 = 85.8732 + 23.4292 = 89.012 m / s2
Newton:
aB=89.012 m/s2
d) Inmediatamente después de pasar
por B la velocidad de la corredera es
prácticamente la misma pero no la aceleración,
ya que la corredera se encuentra en un tramo
horizontal (movimiento rectilíneo) y por tanto
la aceleración será sólo horizontal. Puesto que
cambia la aceleración deben cambiar las
fuerzas, obviamente se modifica el valor de la
normal. Tendremos entonces lo que aparece en
la figura. Aplicamos de nuevo la segunda ley de
kxB cos 45º 400 ⋅ 0.2485 cos 45º
=
= 23.429 m / s2
m
3
aB=23.429 m/s2
ΣFY=maY ⇒ NB+kxBsen45º-mg=0 ⇒ NB=mg-kxBsen45º=
=3 · 9.8-400 · 0.2485sen45º=-40.886 N
Vemos que además del módulo cambia también el sentido de la fuerza, que ahora es
vertical y hacia abajo. Podríamos haberlo deducido del valor de las fueras, ya que el peso de
ΣFX=maX ⇒ kxBcos45º=maB ⇒ aB =
la deslizadera (3 · 9.8=29.4 N) es menor que la reacción del resorte (400 ·
0.2485sen45º=70.286 N) y por tanto tiene que haber otra fuerza en la dirección y sentido
del peso que pueda compensar a la del resorte de modo que no haya aceleración en
dirección vertical. Dicha fuerza es la normal, que valdrá, obviamente:
NB=kxBsen45º-mg=70.286-29.4=40.886 N
NB=40.886 N
1 1 . - Los dos bloques representados en la figura
están unidos mediante un hilo inextensible y sin peso. Se
sueltan partiendo del reposo siendo d=500 mm. Las masas
de los bloques son mA= 6 kg y mB=4 kg y el resorte está
indeformado en la posición inicial. Determinar el mínimo
valor que ha de tener la constante del resorte para que el
bloque B no choque contra el suelo
en el ulterior
movimiento.
Para que el bloque B no choque contra el suelo, tendrá
que llegar a ese punto con velocidad nula. Aplicaremos la
conservación de la energía entre las dos situaciones, la inicial
que aparece en la figura original, y la final cuando el bloque B
llegue justamente al suelo con velocidad nula, de modo que a partir de ahí invertirá el
sentido del movimiento y volverá a ascender. Tomamos como nivel nulo de energía potencial
gravitatoria el suelo. Así, tendremos:
ETinicial+Wotras=ETfinal
Inicialmente
los dos bloques están
en reposo luego no
tienen
energía
cinética, el resorte
está sin deformar
luego no hay energía
potencial elástica y sí
tenemos
energía
potencial gravitatoria,
correspondiente a la
altura del bloque B.
Respecto al trabajo, si consideramos el sistema formado por los dos bloques y la cuerda no
hay ninguna fuerza que realice trabajo ya que sólo actúan los pesos y la fuerza de
recuperación elástica, que son fuerzas conservativas. Y en la posición final tendremos
energía potencial elástica, ya que el resorte está estirado y energía potencial gravitatoria
debido a la altura del bloque A. Es evidente que debido a la disposición de la cuerda siempre
que el bloque B se desplace una cantidad el bloque A se desplazará justo la mitad, ya que
toda la cuerda que sale de la polea en B se recogerá de la polea en A, y en esta polea debe
dividirse en dos tramos iguales. Así, si el bloque B desciende una cantidad d, el bloque A
d
, y por tanto el resorte, que está unido al bloque A, se estira también una
asciende
2
d
. No tendremos en la situación final energía cinética ya que en ese instante los
2
bloques se detienen para invertir el sentido del movimiento. Sustituyendo todo:
1
ETinicial+Wotras=ETfinal ⇒ EPgB=EPe+EPgA ⇒ mB ghB = k∆l2 + mAghA
2
cantidad
mB gd =
2
2
d
1  0.5 
0.5
1 d
⇒ k = 156.8 N / m
k  + mAg ⇒ 4 ⋅ 9.8 ⋅ 0.5 = k
 + 6 ⋅ 9.8 ⋅
2
2  2 
2
2 2
k=156.8 N/m
1 2. - Una corredera B de 4. 5 kg puede
deslizar por una guía horizontal lisa y está en
equilibrio en A cuando recibe un desplazamiento de
1 25 mm hacia la derecha y se suelta. Ambos muelles
tienen una longitud natural de 300 mm y una
constante k=280 N/m. Hallar: a) la velocidad máxima
de la corredera; b) su aceleración máxima; c) la
reacción que ejerce la barra sobre la deslizadera
cuando la aceleración es máxima.
a) Desplazamos el bloque hacia la derecha 125 mm=0.125 m y lo dejamos en
libertad, con lo cual el resorte horizontal está comprimido y empuja a la corredera hacia la
izquierda y el resorte vertical está estirado y tira de la corredera también hacia la
izquierda, de modo que
todas las fuerzas van hacia
la izquierda y son máximas
luego en este punto la
aceleración será máxima. El
bloque empieza a moverse
acelerando y aumentando su
velocidad, hasta pasar por
la posición central en que los resortes están sin deformar y en dirección horizontal no
habría fuerzas y por tanto la aceleración será nula. A partir de ahí la corredera se desplaza
hacia la izquierda pero las fuerzas comienzan a actuar hacia la derecha, con lo cual la
corredera comienza a disminuir su velocidad. Por tanto el punto en que la velocidad es
máxima es aquel en el que la corredera pasa por la posición central. Aplicamos por tanto la
conservación de la energía entre la situación inicial, cuando la deslizadera está en la parte
de la derecha, y la final, cuando pasa por la posición central con velocidad máxima.
Tendremos lo que aparece en la figura. Nos queda:
ETinicial+Wotras=ETfinal
Tomaremos como nivel de energía potencial gravitatoria nulo el de la corredera, que
no varía de altura, y así no tendremos energía potencial gravitatoria ni al principio ni al
final. Inicialmente tenemos energía potencial elástica correspondiente a los dos resortes,
el horizontal (que llamaremos 1) que está comprimido y el vertical (que llamaremos 2) que
está estirado. No tendremos energía cinética porque el sistema parte del reposo. Los
alargamientos de los resortes son:
∆l1=125 mm=0.125 m
∆l2=l2-l0= 0.1252 + 0.3002 − 0.300 = 0.025 m
En cuanto al trabajo realizado por otras fuerzas que no sean ni el peso ni las de
recuperación elástica, sólo actúa la normal, que es perpendicular al desplazamiento y por
tanto no realiza trabajo.
Y en la situación final sólo tendremos energía cinética (velocidad máxima), pero no
potencial elástica puesto que los dos resortes tienen su longitud natural. Así, nos queda:
1
1
1
2
ETinicial+Wotras=ETfinal ⇒ EPelástica1+EPelástica2=EC ⇒ k∆l12 + k∆l22 = mvmáx
2
2
2
vmáx =
(
)
(
)
k ∆l12 + ∆l22
280 0.1252 + 0.0252
=
= 1.01 m / s
m
4.5
vmáx=1.01 m/s
b) Ahora hemos dicho ya que el punto en que la
aceleración es máxima es el inicial, donde las fuerzas que
ejercen los resortes son máximas y están en el mismo
sentido. En esta situación, el ángulo que forma el resorte 2
con la horizontal es:
300
tgθ =
⇒ θ = 67.38º
125
Ahora hacemos el diagrama de sólido
libre de la deslizadera en esa posición, teniendo
en cuenta que está obligada a desplazarse sólo
en dirección horizontal, por lo que la aceleración
sólo tiene componente horizontal. Aplicando la
segunda ley de Newton tendremos:
ΣFX=maX ⇒ k∆l1+k∆l2cosθ=mamáx
k (∆l1 + ∆l2 cos θ)
amáx =
=
m
280(0.125 + 0.025 cos 67.38º )
=
= 8.38 m / s2
4.5
amáx=8.38 m/s2
c) Ahora aplicamos la segunda ley de Newton al otro eje:
ΣFY=maY ⇒ N-mg-k∆l2senθ=0 ⇒ N=mg+k∆l2senθ=4.5 · 9.8+280 · 0.025sen67.38º=50.56 N
N=50.56 N
1 3. Los
dos
bloques
representados en la figura están
unidos mediante un hilo inextensible
y sin peso. Se sueltan, partiendo del
reposo, cuando el resorte está
indeformado. Los coeficientes de
rozamiento estático y cinético valen
0. 3 y 0. 2 respectivamente. Para el
ulterior movimiento determinar: a) la máxima velocidad de los bloques y el
alargamiento que en esa condición sufre el resorte; b) la máxima distancia que
recorrerá el bloque de 1 0 kg hacia abajo por el plano inclinado; c) si rebotarán los
bloques en la posición del apartado b).
a) La constante del resorte vale:
k=1 kN/m=1000 N/m
Llamaremos bloque 1 al de 10 kg y bloque 2 al de 5 kg.
Obviamente en todo momento los dos bloques tienen la misma
velocidad. Puesto que el movimiento es rectilíneo, la máxima velocidad
implica que la aceleración tiene que ser nula (condición de máximo
implica derivada nula). Si hacemos en ese momento los diagramas de
sólido libre de los dos bloques, podremos determinar el alargamiento
en ese instante del resorte y la tensión en la cuerda. Tendremos para
el bloque 1 lo que aparece en la figura, con lo que aplicando la segunda
ley de Newton:
ΣFY=m1a1Y ⇒ N1-m1gcos50º=0 ⇒ N1=m1gcos50º=10 · 9.8cos50º=62.99 N
Como el bloque desliza, la fuerza de rozamiento adquiere su valor máximo:
Fr1=(Fr1)máx=µcN1=0.2 · 62.99=12.60 N
Y en el otro eje:
ΣFX=m1a1X ⇒m1gsen50º-Fr1-T=0 ⇒ T=m1gsen50º-Fr1=10 · 9.8sen50º-12.60=62.47 N
Ahora vamos al bloque 2, para el que hacienda lo
mismo tendremos:
ΣFY=m2a2Y ⇒ N2-m2g=0 ⇒ N2=m2g=5 · 9.8=49 N
Puesto que el bloque desliza la fuerza de
rozamiento adquiere su valor máximo:
Fr2=(Fr2)máx=µcN2=0.2 · 49=9.8 N
Por último nos queda:
T − Fr2
ΣFX=m2a2X ⇒ T-Fr2-k∆x=0 ⇒ ∆x =
=
k
62.47 − 9.8
=
= 0.0527 m
1000
Ya tenemos el alargamiento del resorte en en instante en que la velocidad es
máxima:
∆x=0.0527 m
Ahora vamos a calcular esa velocidad. Para ello aplicamos la conservación de la
energía entre la situación inicial, que llamaremos 1, donde los móviles parten del reposo con
el resorte sin deformar, y la situación final, que llamaremos 2 en la que la velocidad de los
bloques es máxima y el alargamiento del resorte es de 0.0527 m. Obviamente como el
resorte inicialmente está con su longitud inicial, si se alarga 0.0527 m es porque los dos
bloques se desplazan justo esa cantidad. Tendremos lo que aparece en el gráfico.
Aplicando el teorema de conservación de la energía:
ET1+Wotras=ET2
No vamos a tener en cuenta la energía potencial gravitatoria del bloque 2 porque no
varía su altura, luego es igual en la situación 1 y en la 2 y podemos obviarla. Inicialmente
solo tenemos energía potencial gravitatoria del bloque 1. En cuanto al trabajo realizado por
otras fuerzas diferentes al peso y a la de recuperación elástica, están las normales, que no
realizan trabajo porque son perpendiculares al desplazamiento, y las fuerzas de
rozamiento, que sí realizan trabajo porque se desplazan 0.0527 m con los bloques. Y en la
situación final tendremos energía cinética correspondiente a los dos bloques porque su
velocidad es máxima y energía potencial elástica ya que el resorte está alargado 0.0527 m.
Así pues:
ET1+Wotras=ET2 ⇒ EPg1+WFr1+WFr2=EC1+EC2+EPe2
1
1
1
2
2
m1 gh 1 + Fr1 ⋅ x1 + Fr2 ⋅ x2 = m1 vmáx
+ m2vmáx
+ k∆x2
2
2
2
1
1
2
m1g∆xsen50º +Fr1 ∆x cos 180 º +Fr2 ∆x cos 180 º = (m1 + m2 )vmáx
+ k∆x2
2
2
1
1
2
2
m1 g∆xsen50º −Fr1 ∆x − Fr2 ∆x − k∆x = (m1 + m2 )vmáx
2
2
vmáx
1


2 m1 g∆xsen50 º −Fr1 ∆x − Fr2 ∆x − k∆x2 
2

 =
=
m1 + m2
1


2 10 ⋅ 9.8 ⋅ 0.0527 sen50º −12.60 ⋅ 0.0527 − 9.8 ⋅ 0.0527 − 1000 ⋅ 0.0527 2 
2

 = 0.430 m / s
=
10 + 5
vmáx=0.430 m/s
b) Ahora vamos a ver cuál es la máxima distancia que recorre el bloque. Llamamos a
esta distancia ∆xmáx, ya que coincide con lo que se alarga el resorte. Puesto que es la
máxima distancia, en ese instante los bloques se detienen e invierten el sentido del
movimiento, luego en esa situación, que llamaremos situación 3, la velocidad de los bloques
es nula. Aplicamos de nuevo la conservación de la energía, teniendo en cuenta que
básicamente es como en el apartado anterior pero la energía cinética final es nula porque
los bloques se detienen:
ET1+Wotras=ET3 ⇒ EPg1+WFr1+WFr2=EPe3
1
2
m1 gh 3 + Fr1 ⋅ x1 + Fr2 ⋅ x2 = k∆xmáx
2
1
2
m1 g∆xmáx sen50º +Fr1 ∆xmáx cos 180 º +Fr2 ∆xmáx cos 180 º = k∆xmáx
2
2(m1 gsen50º −Fr1 − Fr2 )
1
m1 gsen50º −Fr1 − Fr2 = k∆xmáx ⇒ ∆xmáx =
=
2
k
2(10 ⋅ 9.8sen50 º −12.60 − 9.8)
=
= 0.1053 m
1000
∆xmáx=0.1053 m
c) Veamos qué ocurre en esta
posición. Supongamos que los bloques sí
rebotan. En este caso, el bloque 1
comenzará a subir y el bloque 2 tendrá que
ir hacia la izquierda, luego ambos tendrán
aceleración en ese sentido para iniciar de
nuevo el movimiento partiendo del reposo. El
diagrama de sólido libre del bloque 1 sería
entonces el de la figura. Aplicando la
segunda ley de Newton:
ΣFY=m1a1Y ⇒ N1-m1gcos50º=0 ⇒ N1=m1gcos50º=10 · 9.8cos50º=62.99 N
Para que el bloque comience a moverse tiene que superar la fuerza de rozamiento
estática, luego tiene que adquirir el valor:
Fr1=(Fr1)máx=µeN1=0.3 · 62.99=18.90 N
ΣFX=m1a1X ⇒ Fr1+m1gsen50º-T=-m1a ⇒ T-18.90-10 · 9.8sen50º=10a ⇒ T-93.97=10a
Igualmente hacemos el diagrama
de sólido libre del bloque 2 y operamos de
modo similar:
ΣFY=m2a2Y ⇒ N2-m2g=0
N2=m2g=5 · 9.8=49 N
Fr2=(Fr2)máx=µeN2=0.3 · 49=14.7 N
ΣFX=m2a2X ⇒ T+Fr2-k∆xmáx=-m2a
1000 · 0.1053-T-14.7=5a ⇒ 90.6-T=5a
Tenemos dos ecuaciones y dos
incógnitas. Sumando las dos ecuaciones:
T − 93.97 = 10 a 
2
 ⇒ −3.37 = 15a ⇒ a = −0.225 m / s
90.6 − T = 5a 
La solución a la que llegamos es absurda, la aceleración sería en sentido contrario,
con lo cual ese punto no sería el de máximo alargamiento. Esto quiere decir que la
suposición hecha no es correcta el los bloques no rebotan.
NO REBOTAN
Veamos qué se obtiene si hacemos la suposición contraria. Supongamos que los
bloques se detienen en ese punto y ya no rebotan. En este caso los bloques permanecerían
en equilibrio y no habría aceleración, y además como no hay deslizamiento las fuerzas de
rozamiento deberían ser inferiores a su valor máximo:
Fr1<(Fr1)máx ⇒ Fr1<µeN1
Fr2<(Fr2)máx ⇒ Fr2<µeN2
Tendremos lo que aparece en el gráfico para el bloque 1:
ΣFY=m1a1Y ⇒ N1-m1gcos50º=0
N1=m1gcos50º=10 · 9.8cos50º=62.99 N
ΣFX=m1a1X ⇒ T-Fr1-m1gsen50º=0 ⇒ T-Fr1-10 · 9.8sen50º=0
T-Fr1-75.07=0
Para el bloque 2 hacemos de modo similar y tendremos:
ΣFY=m2a2Y ⇒ N2-m2g=0 ⇒ N2=m2g=5 · 9.8=49 N
ΣFX=m2a2X ⇒ T+Fr2-k∆xmáx=0
T+Fr2-1000 · 0.1053=0 ⇒ T+Fr2-105.3=0
Restamos las dos ecuaciones obtenidas:
T − Fr1 − 75.07 = 0 
 ⇒ Fr1 + Fr2 − 30.23 = 0 ⇒ Fr1 + Fr2 = 30.23
T + Fr2 − 105.3 = 0 
Comprobamos la suposición hecha inicialmente, que
es que las fuerzas de rozamiento tienen que ser inferiores
a sus valores máximos:
Fr1<µeN1 ⇒ Fr1<0.30 · 62.99 ⇒ Fr1<18.90 N
Fr2<µeN2 ⇒ Fr2<0.30 · 49 ⇒ Fr2<14.70 N
Por tanto debe verificarse que:
Fr1+Fr2<18.90+14.70 ⇒ Fr1+Fr2<33.60 ⇒ 30.23<33.60
Vemos que lo que obtenemos es correcto, luego la
suposición que hemos hecho es cierta y los bloques no rebotan.
NO REBOTAN
1 4. - Un cochecito de juguete desciende
por una rampa y sigue luego un rizo vertical
según se indica en la figura. La masa del
cochecito es m=50 g y el diámetro del rizo
vertical es d=300 mm. Si se suelta el cochecito
partiendo del reposo, determinar: a) la mínima
altura h desde la que hay que soltar el cochecito
para que recorra todo el rizo; b) la fuerza que el
cochecito ejerce sobre la pista cuando se halla
en el punto B (un cuarto del rizo).
a) En el Sistema Internacional tendremos los datos:
m=50 g=0.050 kg
d=300 mm ⇒ r=150 mm=0.15 m
El punto crítico de la trayectoria es el punto más alto del rizo,
ya que una vez pasado este punto el móvil recorrería el resto
simplemente bajo la acción de la gravedad. Vamos a ver por tanto con
qué velocidad debe llegar el cochecito al punto más alto de la
trayectoria, punto que llamaremos C. Hacemos el diagrama de sólido
libre del coche en el punto C y tendremos la gráfica adjunta.
Obviamente la mínima altura en el punto A implicará la mínima velocidad
en el punto C y por tanto la mínima aceleración normal anC. Vemos que la
aceleración centrípeta está proporcionada por dos fuerzas, el peso y la
normal, que tienen el mismo sentido, luego la aceleración centrípeta será
tanto menor cuanto menor sean estas dos fuerzas. El peso es constante,
y el menor valor de la normal es cero puesto que no puede cambiar de
sentido. Así pues, la menor velocidad en C y por tanto la menor altura en
A implica que la normal en el punto más alto de la trayectoria es nula.
Tendremos entonces la figura que aparece al lado, y aplicamos la
segunda ley de Newton en la dirección normal:
vC2
⇒ vC2 = gr
r
Ahora aplicamos la conservación de la
energía entre los puntos A y C:
ETA+Wotras=ETC
En el punto A sólo tenemos energía
potencial gravitatoria debida a la altura h. En
cuanto al trabajo de las fuerzas, aparte del peso
aparece sólo la normal, que es perpendicular al
desplazamiento y no realiza trabajo. Y en el
punto C tenemos energía potencial porque la
altura es d y energía cinética porque la velocidad
ΣFn=man ⇒ mg=manC ⇒ g =
del coche es vC. Así pues nos queda:
1
1
mv 2 ⇒ gh = gd + gr
2 C
2
5r 5 ⋅ 0.15
2h=2d+r ⇒ 2h=2 · 2r+r ⇒2h=5r ⇒ h =
=
= 0.375 m
2
2
h=0.375 m
b) Ahora vamos al punto B. Para saber la
velocidad que tiene el cochecito en el punto B
ETA+Wotras=ETC ⇒ EPgA=EPgC+ECC ⇒ mghA = mghC +
aplicamos la conservación de la energía entre los puntos A y B. Operamos de modo análogo a
como hemos hecho antes y tendremos:
ETA+Wotras=ETB ⇒ EPgA=EPgB+ECB
1
mghA = mghB + mvB2
2
1 2
5r
2
gh = gr + vB ⇒ vB = 2gh − 2gr = 2g
− 2gr = =5gr-2gr=3gr
2
2
Ahora hacemos el diagrama de sólido libre del cochecito
en el punto B y tendremos:
v2
3gr
ΣFn=man ⇒NB=manB= m B = m
= 3mg = 3 · 0.050 · 9.8=1.47 N
r
r
NB=1.47 N
1 5. - Una cantante hace girar un micrófono de
0. 35 kg situado en el extremo de un hilo de 750 mm
de longitud, en un plano vertical. Determinar: a) la
mínima celeridad que debe tener el micrófono en la
posición A para poder recorrer toda la trayectoria
circular; b) la máxima tensión del hilo.
a) Obviamente el punto crítico de la trayectoria
es el punto B, el más alto, ya que a partir de ahí la
trayectoria se cerraría bajo la acción de la gravedad.
Realizamos un diagrama de sólido libre en el punto B para
ver las fuerzas que actúan sobre el micrófono en esa
situación y tendremos lo que aparece en la figura adjunta.
Es evidente que si queremos que la velocidad en A sea
mínima, la velocidad en B también será mínima y por tanto
deberá ser mínima la aceleración normal anB. Dicha
aceleración está proporcionada por dos fuerzas de la
misma dirección y sentido, luego estas fuerzas deberán
también ser mínimas. El peso es constante, deberá ser
mínima la tensión, y el menor valor de la tensión es el
cero. Así pues, la velocidad tanto en A como en B será
mínima cuando la tensión en el punto B sea nula. Así
pues, aplicando todo lo dicho tendremos:
v2
ΣFn=man ⇒ mg+TB=manB ⇒ mg = m B ⇒ vB2 = gr
r
Ahora aplicamos la conservación de la energía
entre la posición A, donde la velocidad será mínima, y la
posición B, donde ya conocemos la velocidad:
ETA+Wotras=ETB
En la situación A la energía es sólo cinética. En cuanto al trabajo, aparte del peso
actúa sólo la tensión, que es perpendicular al desplazamiento y no realiza trabajo. Y en la
situación B el micrófono posee tanto energía cinética como potencial. Sustituyendo:
1
1
1 2
1
ETA+Wotras=ETB ⇒ ECA=ECB+EPgB ⇒ mvA2 = mvB2 + mghB ⇒ vmín
= vB2 + 2gr
2
2
2
2
vmín = vB2 + 4gr = gr + 4gr = 5gr = 5 ⋅ 9.8 ⋅ 0.75 = 6.06 m / s
vmín=6.06 m/s
b) Para determinar en qué punto
la tensión es máxima vamos a realizar el
diagrama de sólido libre del micrófono
en una posición genérica. Aplicando la
segunda ley de Newton tendremos:
ΣFn=man ⇒ T-mgcosθ=man

v2
v2 
T = mg cos θ + m
= m g cos θ +
r
r 

Si en vez de en la parte inferior
de la trayectoria el micrófono está en la
parte superior la tensión y el peso
tienen el mismo sentido (ver figura), con
lo cual nos quedaría:
ΣFn=man ⇒ T+mgcosθ=man

v2
v2 
T = mg cos θ − m
= m g cos θ −
r
r 

De las dos opciones, es obvio que la tensión es mayor en el primer caso, donde
sumamos dos términos, y no en el segundo donde los restamos. Y en este caso, donde la

v2 
el valor será máximo cuando el coseno sea máximo:
tensión vale m g cos θ +
r 

cosθ=1 ⇒ θ=0º
Por tanto el valor máximo de la tensión es en el punto más bajo de la trayectoria
(punto A) y vale:


5gr 
v2 
v2 

Tmáx = m g cos θ + A  = m g + A  = m g +
 = m(g + 5g) = 6mg = 6 ⋅ 0.35 ⋅ 9.8 = 20.58 N
r 
r 
r 



Tmáx=20.58 N
1 6. - Una deslizadera de 7 kg se desplaza sin
rozamiento a lo largo de una barra que forma un ángulo
de 30º con la vertical. Cuando la deslizadera está
situada en el punto A, el muelle de constante k=1 50
N/m no presenta deformación. Determinar la velocidad
y la aceleración de la deslizadera en el punto B si se
suelta desde el reposo en el punto A.
En primer lugar calculamos las condiciones
geométricas del problema. El triángulo ABC es isósceles,
luego tiene dos ángulos iguales (α). Evidentemente el ángulo
que nos queda en el vértice B también tiene que ser α, luego
tendremos que:
2α=60º ⇒ α=30º
Y puesto que los ángulos de un triángulo suman 180º:
θ=180º-2α=180º-2 · 30º=120º
Calculemos ya la longitud del resorte aplicando el
teorema del coseno:
2
2
BC = l = AC + AB − 2AB AC cos θ =
= 0.52 + 0.52 − 2 ⋅ 0.5 ⋅ 0.5 cos 120º = 0.866 m
El resorte en la posición B está alargado una cantidad:
∆lB=l-l0=0.866-0.5=0.366 m
Aplicamos
el
teorema
de
conservación de la energía entre la situación
A, cuando la deslizadera parte del reposo, y
B, cuando su velocidad es vB. Tendremos:
ETA+Wotras=ETB
En A sólo tenemos energía potencial
gravitatoria, correspondiente a una altura h,
mientras que en B tenemos energía cinética
y energía potencial elástica. En cuanto al
trabajo realizado por las fuerzas, aparte
del peso y la fuerza de recuperación
elástica, que son conservativas, sólo actúa la
normal, que por ser perpendicular al desplazamiento no realiza trabajo:
1
1
ETA+Wotras=ETB ⇒ EPgA=ECB+EPeB ⇒ mgh = mvB2 + k∆lB2
2
2
1
1
7 ⋅ 9.8 ⋅ 0.5sen60º = 7 vB2 + 150 ⋅ 0.3662 ⇒ vB = 2.37 m / s
2
2
vB=2.37 m/s
Ahora queremos la aceleración
de la deslizadera en el punto B. Aislamos la deslizadera.
Sobre ella actúan el peso, vertical y hacia abajo, la
reacción del resorte, que es de tensión, y la normal,
perpendicular a la barra. Y la aceleración, puesto que el
movimiento es rectilíneo, tendrá la dirección de la
barra. Aplicando la segunda ley de Newton al eje X:
ΣFX=maBX ⇒ mgcos30º-k∆lBcos30º=maB
7 · 9.8cos30º-150 · 0.36cos30º=7aB ⇒ aB=1.69 m/s2
aB=1.69 m/s2
1 7. Una partícula se
mueve a lo largo de una línea
donde la energía potencial depende
de su posición r como aparece en
la figura. a) Identifique cada
posición de equilibrio para esta
partícula,
indicando
si
dicho
equilibrio es estable, inestable o
neutro; b) ¿para qué rango de
energía total la partícula estará
oscilando? c) Ahora suponga que la
partícula tiene una energía de - 3
J.
Determine
el
rango
de
posiciones donde puede encontrarse, su máxima energía cinética y la ubicación en que
tiene máxima energía cinética.
decir:
a) Tenemos movimiento en una dimensión, donde la fuerza deriva del potencial, es
dU
dx
Si la partícula está en equilibrio, F=0, luego:
dU
dU
F=0⇒−
=0⇒
=0
dx
dx
F=−
ahora el tipo de equilibrio en cada caso.
Gráficamente la derivada de
una función en un punto es la
pendiente de la tangente a la curva
en ese punto, luego si la pendiente es
nula, la tangente tiene que ser
horizontal. Los puntos de equilibrio
son aquéllos en los que la tangente a
la curva es horizontal, es decir, en
los máximos, mínimos o tramos
rectos de la curva de potencial, como
puede verse en la gráfica. Tenemos
los puntos marcados. Vamos a ver
Comencemos por los puntos
que se encuentran en los mínimos de
la curva de potencial, que tienen
idéntico razonamiento (puntos 1 y 3).
Razonamos para el punto 1. Si
desplazamos la partícula hacia la
izquierda (r negativo) la pendiente
de la tangente es negativa, lo cual
significa que la fuerza es positiva
(hacia la derecha) y hace volver a la
partícula a la posición de equilibrio.
Análogamente sucede si desplazamos
la partícula hacia la derecha (r positivo). En este caso la pendiente de la tangente es
positiva, lo que significa que aparece una fuerza negativa (hacia la izquierda), que devuelve
también la partícula a la posición de equilibrio. En resumen, cualquier desplazamiento que
realicemos sobre la partícula hace aparecer una fuerza de sentido opuesto al
desplazamiento que devuelve a la partícula a la posición de equilibrio. Estos puntos son por
tanto de equilibrio estable.
r1=1.5 mm y r3=3.2 mm ⇒ equilibrio estable
Ahora vamos a ver qué ocurre cuando el punto corresponde con un máximo de la
curva de potencial (punto 2). En este caso, si desplazamos la partícula a la izquierda de la
posición de equilibrio (r negativo) la pendiente de la tangente es positiva, lo que significa
que aparece una fuerza negativa (hacia la izquierda) que aleja a la partícula de la posición
de equilibrio. Del mismo modo, si desplazamos la partícula hacia la derecha (r positivo) la
pendiente de la tangente es negativa, lo cual significa que aparece una fuerza positiva
(hacia la derecha) que aleja a la partícula de la posición de equilibrio. En conclusión, sea cual
sea el sentido del desplazamiento, siempre aparece una fuerza en ese mismo sentido que
aleja la partícula de la posición de equilibrio, luego se trata de equilibrio inestable.
r2=2.3 mm ⇒ equilibrio inestable
Por último estudiamos el tramo horizontal. Aquí es evidente que al desplazar la
partícula en cualquier sentido la tangente sigue siendo horizontal, lo cual significa que la
pendiente, y por tanto la fuerza, es nula. La partícula queda de nuevo en reposo: el
equilibrio es indiferente o neutro.
r4>5 mm neutro
b) Para que la partícula oscile
tiene que tener dos puntos de
retorno, es decir, dos puntos en los
que se detenga (velocidad nula y por
tanto energía cinética nula) e
invierta el sentido del movimiento. Si
la energía cinética es nula toda la
energía es potencial. La energía total
(que por ser constante tiene que
venir
representada
por
una
horizontal) coincide con la potencial,
luego estas dos gráficas se cortan.
Esto sucede, como vemos en la gráfica, para energías entre -5.6 J y 1 J aproximadamente.
Por encima de esa energía sólo hay un punto de retorno a la izquierda y el movimiento no
sería oscilatorio, sino que la partícula al moverse hacia la derecha seguiría hasta el infinito.
-5.6 J<E<1 J
c) Ahora tenemos una
energía total de -3 J, tal como
representamos en la gráfica por
una horizontal en -3 J. La energía
total es constante, y es suma de la
cinética más la potencial:
ET=EC+U
La energía cinética es
siempre positiva, luego tendremos:
EC=ET-U ⇒ EC>0 ⇒ ET-U>0 ⇒ ET>U
Sólo son posibles los
movimientos donde la energía total
está por encima de la potencial,
luego la recta que representa la energía total tiene que estar siempre por encima de la
curva de potencial. Así, el movimiento estará permitido sólo entre los puntos A y B, es
decir, leyendo sobre la recta de distancias:
0.6 mm<r<3.6 mm
Puesto que la energía total
es constante, la máxima energía
cinética tiene que corresponder
con la mínima energía potencial, es
decir, la correspondiente al punto
que marcamos como 1. Leyendo
sobre la gráfica tendremos que en
este punto:
U1=-5.6 J
es:
Aplicando la conservación de la energía:
ET=EC1+U1
EC1=ET-U1=-3-(-5.6)=2.6 J
EC1=2.6 J
Y leyendo en el eje de distancias, la posición en que la energía cinética es máxima
r1=1.5 mm
1 8. - Considere el diagrama de energía
mostrado en la figura. a) ¿Cuáles son los límites
del movimiento cuando las energías son E1 y E2?
Haga un nuevo diagrama y nombre sus partes. b)
Describa las circunstancias bajo las cuales la
partícula siempre está en reposo; c) determine las
energías y posiciones para las cuales es posible el
movimiento dentro de los puntos de retorno; d)
determine las posiciones de equilibrio en la figura.
¿Son estables o inestables?
a) Como hemos visto en el problema anterior, sólo están permitidos los movimientos
en aquellos puntos en los que la recta que representa la energía total está por encima de la
curva de potencial. Así, para la energía E1 está permitido el movimiento para valores de x
comprendidos entre los correspondientes a los puntos A y B, entre los puntos C y D y por
encima de E. Del mismo modo, cuando la energía es E2 el movimiento es posible para valores
de x por encima del correspondiente a F.
b) Si la partícula está en reposo implica que la energía cinética es nula, y de acuerdo
con la conservación de la energía:
ET=EC+U ⇒ EC=0 ⇒ ET=U
Esto quiere decir que la recta de energía total y la curva de potencial coinciden
siempre. Esto sólo puede suceder si la recta de energía total es tangente a la curva de
potencial, y por tanto la corta en un solo punto. Esto se producirá para los casos en que la
energía total de la partícula corresponda a la de los puntos G,H,I ó J.
c) Si queremos que la partícula se mueva oscilando entre dos puntos de retorno la
recta que representa la energía total tiene que cortar a la curva de potencial en dos
puntos, lo cual sólo ocurre si la recta de energía total está por debajo del punto J. Por
tanto, el movimiento entre dos puntos de retorno es posible sólo para energías totales por
debajo de la correspondiente al punto J. Obviamente, las posiciones serán las que estén a la
izquierda del punto J.
d) De acuerdo a lo explicado en el problema anterior, los puntos de equilibrio son los
correspondientes a los máximos y mínimos de la curva de potencial, siendo los máximos
puntos de equilibrio inestable y los mínimos puntos de equilibrio estable. Por tanto, los
puntos H y J corresponden a puntos de equilibrio inestable mientras que los puntos G e I
implican puntos de equilibrio estable.
1 9. - La función energía potencial de una partícula de masa 4 kg en un campo
de fuerzas viene descrita por:
U=3x2- x3
x≤3 m
U=0
x> 3 m
en donde U se expresa en julios y x en metros. a) ¿Para qué valores de x la fuerza F
es cero? b) Hacer un esquema de U en función de x; c) discutir la estabilidad del
equilibrio para los valores de x obtenidos en a); d) si la energía total de la partícula
es de 1 2 J, ¿cuál será su velocidad en x=2 m?
a) Tenemos que la fuerza deriva del potencial, de modo que para x≤3 m:
dU
d
F=−
=−
(3x2 − x3 ) = 3x2 − 6x
dx
dx
Y para x>3 m:
dU
d
F=−
=−
(0) = 0
dx
dx
Y entonces si la fuerza es nula tendremos que para x≤3 m:
x=0

F=0 ⇒ 3x2-6x=0 ⇒ x(3x-6)=0 ⇒ 
3x − 6 = 0 ⇒ x = 2 m
Y en el otro intervalo la fuerza es nula, luego tendremos que la fuerza es cero para:
x=0; x=2 m; x>3 m
b)
Se
trata
de
hacer
la
representación gráfica. Obviamente por
encima de 3 m la energía potencial es nula,
luego no hace falta que demos valores. Por
debajo de 3 m tendremos la tabla:
x (m) U (J)
x (m) U (J)
-1
4
1.5
3.375
-0.5 0.875
2
4
0
0
2.5
3.125
0.5
0.625
3
0
1
2
Tendremos la gráfica que aparecen en la figura.
c) Como hemos visto en los problemas anteriores, el equilibrio es estable si la curva
de potencial pasa por un mínimo, inestable si pasa por un máximo e indiferente si la curva es
horizontal. Así pues, a la vista de la gráfica tendremos:
x=0 ⇒ equilibrio estable; x=2 m ⇒ equilibrio inestable; x>3 m ⇒ equilibrio indiferente
d) Para x=2 m podemos determinar la energía potencial:
U(2)=3x2-x3=3 · 22-23=4 J
Por diferencia obtenemos la cinética:
ET=EC+U ⇒ EC=ET-U=12-4=8 J
Y de aquí la velocidad:
EC =
1
mv2 ⇒ v =
2
2EC
=
m
v=2 m/s
2⋅8
= 2 m/s
4
20. - La energía potencial de un objeto viene dada por U(x)=8x2- x4 en donde U
se expresa en Julios y x en metros. a) Determinar la fuerza que actúa sobre ese
objeto; b) ¿en qué posiciones el objeto se encuentra en equilibrio? c) ¿Cuáles de estas
posiciones de equilibrio son estables y cuáles son inestables? d) ¿Cuáles son los puntos
de retorno correspondientes a una energía total de 2 J?
a) Puesto que la fuerza deriva del potencial:
dU
d
=−
F=−
(8x2 − x 4 ) = − 16x − 4 x3 = 4 x3 − 16x
dx
dx
F=4x3-16x
b) Si el objeto está en equilibrio:
4x = 0 ⇒ x = 0


F=0 ⇒ 4x3-16x=0 ⇒ 4x(x2-4)=0 ⇒ x2 − 4 = 0 ⇒ x = 4 =

(
)
2

− 2
x=0; x=2 m; x=-2 m
c) Veamos ahora el tipo de equilibrio. De acuerdo a lo dicho hasta ahora, si tenemos
un máximo en la curva de potencial el equilibrio es inestable mientras que si tenemos un
mínimo el equilibrio es estable. Analíticamente, la diferencia entre un máximo y un mínimo
está en el signo de la segunda derivada, si la segunda derivada es positiva nos encontramos
en un mínimo, si es negativa nos encontramos en un máximo. Así pues tendremos:
U=8x2-x4 ⇒ U’=16x-4x3 ⇒ U’’=16-12x2
Ahora en los tres puntos que tenemos:
U(0)= 16-12x2=16>0 ⇒ Mínimo ⇒ Equilibrio estable
U(2)= 16-12x2=16-12 · 22=-32<0 ⇒ Máximo ⇒ Equilibrio inestable
U(-2)= 16-12x2=16-12 · (-2)2=-32<0 ⇒ Máximo ⇒ Equilibrio inestable
Por tanto:
x=0 estable; x=±2 m inestable
d) Los puntos de retorno son aquellos puntos en que la partícula se detiene
momentáneamente e invierte el sentido del movimiento. En ellos la energía cinética es nula,
lo cual implica que la potencial coincide con la total:
ET=EC+U ⇒ EC=0 ⇒ ET=U ⇒ 2=8x2-x4 ⇒ x4-8x2+2=0
Tenemos una ecuación bicuadrada. Hacemos el cambio de variable x2=y:
x4-8x2+2=0 ⇒ y2-8y+2=0 ⇒ y =
8 ± 82 − 4 ⋅ 2 7.742
=
2
0.258
Y deshaciendo el cambio de variable:

 2.782
 7.742 = 

− 2.782
x2 = y ⇒ x = y = 
 0.258 =  0.508

− 0.508
x=±2.78 m; x=±0.508 m