Grandes depósitos y el riesgo de liquidez bancario
Anuncio

*UDQGHVGHSyVLWRV\HOULHVJRGHOLTXLGH]EDQFDULR
8QDDSUR[LPDFLyQPHGLDQWHODGRPLQDQFLDHVWRFiVWLFD
0DUWtQ(JR]FXH
5HVXPHQ
(QHVWHHVWXGLRDQDOL]DPRVVLODFRQFHQWUDFLyQHQ ORV GHSyVLWRV SXHGH DIHFWDU DO
ULHVJRGHOLTXLGH]EDQFDULR
(Q OD DFWXDOLGDG H[LVWHQ GLVSRVLFLRQHV TXH QRUPDQ OD FRQFHQWUDFLyQ GH ORV
FUpGLWRV EDQFDULRV 6LQ HPEDUJR OD UHJXODFLyQ HQ OD FRQFHQWUDFLyQ GH ORV SDVLYRV
EDQFDULRV KD VLGR UHOHJDGD D XQ VHJXQGR SODQR 8Q UHJXODGRU SUXGHQFLDO QR GHEHUtD
GHMDUGHODGRORVSRVLEOHVHIHFWRVQHJDWLYRVTXHSXGLHUDQDFDUUHDUODIXJDLQHVSHUDGDGH
JUDQGHVGHSyVLWRV
3RUORWDQWRFRQVWLWX\HXQREMHWLYRGHHVWHWUDEDMRWUDQVPLWLUHVWDLQTXLHWXG\
GHPRVWUDU TXH OD FRQFHQWUDFLyQ HQ HO ILQDQFLDPLHQWR HIHFWLYDPHQWH HV XQD HVWUDWHJLD
GH ULHVJR 3DUD HVWH SURSyVLWR VH GHPXHVWUD XQ WHRUHPD VREUH GRPLQDQFLD HVWRFiVWLFD
GH VHJXQGR RUGHQ SDUD FRPELQDFLRQHV OLQHDOHV FRQYH[DV GH YDULDEOHV DOHDWRULDV 6H
SUXHED TXH FXDQWR PiV FRQFHQWUDGRV HVWpQ ORV GHSyVLWRV PiV ULHVJRVD VH YXHOYH OD
GLVWULEXFLyQGHORVUHWLURVEDQFDULRV
$GHPiV VH PXHVWUD TXH XQ %DQFR &HQWUDO SUHIHULUi WHQHU XQ VLVWHPD ILQDQFLHUR
FRQGHSyVLWRVEDQFDULRVWDQDWRPL]DGRVFRPROHVHDSRVLEOH3RUHVWHPRWLYRORVQLYHOHV
GHHQFDMHVILMDGRVSRUHO%DQFR&HQWUDOGHEHUtDQVHUPD\RUHVFXDQWRPiVVHFRQFHQWUHQ
ORVGHSyVLWRV
1
7UDEDMR SUHVHQWDGR FRPR 7HVLV GH 0DHVWUtD HQ (FRQRPtD ,QWHUQDFLRQDO SUHVHQWDGD HQ OD )&6 8'(/$5 4XLVLHUD
DJUDGHFHU OD JXtD GH-XDQ 'XEUD \ ORV FRPHQWDULRV GH $OYDUR )RUWH]D -RVp $QWRQLR /LFDQGUR $OHMDQGUR 3HQD \ (GXDUGR
6LDQGUD/DUHVSRQVDELOLGDGSRUSRVLEOHVHUURUHV\RPLVRQHVVRQPtDV
,1752'8&&,21
(OULHVJRGHOLTXLGH]EDQFDULRVHSURGXFHFXDQGRXQEDQFRQRWLHQHODVUHVHUYDVOtTXLGDV
VXILFLHQWHV SDUD FXPSOLU FRQ VXV REOLJDFLRQHV ILQDQFLHUDV 3RU VHU HVWD XQD PDOD VHxDO
SDUDHOUHVWRGHORVGHSRVLWDQWHV\GHELGRDHOORSRUODSRVLELOLGDGGHFRQWDJLRHQWUHODV
LQVWLWXFLRQHVILQDQFLHUDVHOULHVJRGHOLTXLGH]VHDXQDGHODVPD\RUHVSUHRFXSDFLRQHVGH
ORV UHJXODGRUHV GH VLVWHPDV ILQDQFLHURV /D H[LVWHQFLD GH XQ SUHVWDPLVWD GH ~OWLPD
LQVWDQFLDTXHHQJHQHUDOHVHO%DQFR&HQWUDOGHWHUPLQDTXHORVULHVJRV DVRFLDGRV D OD
DFWLYLGDG EDQFDULD VHDQ GLItFLOHV GH LQWHUQDOL]DU 3RU HVWD UD]yQ ORV UHJXODGRUHV GH
VLVWHPDVILQDQFLHURVH[LJHQDVXVLQVWLWXFLRQHVHOFXPSOLPLHQWRGHFLHUWDVQRUPDV
(VWDV QRUPDV WLHQHQ FRPR FRPHWLGR SULQFLSDO UHVWULQJLU OD OLEUH HOHFFLyQ GHO SRUWDIROLR
EDQFDULR8QDGHHVWDVUHVWULFFLRQHVFRQVLVWHHQUHTXHULUHQFDMHVPtQLPRVREOLJDWRULRV (Q JHQHUDO OD GHWHUPLQDFLyQ GH ORV HQFDMHV PtQLPRV REOLJDWRULRV GHSHQGH GHO PRQWR \
GHO YHQFLPLHQWR GH ORV GHSyVLWRV (O OLEUR ,, GH OD 5HFRSLODFLyQ GH 5HJXODFLyQ \ &RQWURO
GHO VLVWHPD ILQDQFLHUR SDUFLDOPHQWH GHURJDGR \ OD FLUFXODU 1 GHO GHO
%DQFR &HQWUDO GHO 8UXJXD\ TXH UHJXODQ ORV HQFDMHV PtQLPRV REOLJDWRULRV QR WLHQH HQ
FXHQWD SDUD VXFiOFXOR OD SRVLEOH FRQFHQWUDFLyQ GH ORV GHSyVLWRV HQ SRFDV ´PDQRVµ $
WDOSXQWRTXHGRVEDQFRVFRQLJXDOPRQWRPRQHGD\HVWUXFWXUDGHYHQFLPLHQWRVGHVXV
GHSyVLWRV WHQGUtDQ XQD H[LJHQFLD GH HQFDMHV GH OD PLVPD FXDQWtD (VWR QR SDUHFH PX\
OyJLFRSXHVGHEHUtDH[LVWLUXQPD\RUULHVJRDPD\RUFRQFHQWUDFLyQGHGHSyVLWRV
(O LQFUHPHQWR HQ HO ULHVJR RSHUDUtD GH OD VLJXLHQWH IRUPD VXSRQJDPRV XQ EDQFR TXH
WLHQH GHSyVLWRV PX\ FRQFHQWUDGRV SRQJDPRV XQ FDVR H[WUHPR DXQTXH QR LUUHDO TXH
FRQWDUD FRQ XQ VROR GHSRVLWDQWH (VH ~QLFR GHSRVLWDQWH SXHGH UHFLELU XQ VKRFN
LQHVSHUDGR GH OLTXLGH] \ H[LJLU OD GHYROXFLyQ WRWDO GHO SDVLYR EDQFDULR 3DUHFH PHQRV
SUREDEOHFRQWDOQLYHOGHJUDYHGDGTXHDQWHHOPLVPRVKRFNGHOLTXLGH]HOORRFXUUDHQ
XQDVLWXDFLyQGHDWRPL]DFLyQGHORVGHSyVLWRV (Q OD OLWHUDWXUD HFRQyPLFD HO ULHVJR SRU OD SUHVHQFLD GH JUDQGHV LQYHUVRUHV \D KD VLGR
DQDOL]DGR SDUD HO FDVR GH FRUULGDV FDPELDULDV YpDVH &RUVHWWL 'DVJXSWD 0RUULV \ 6KLQ
2
/DUD]yQGHORVHQFDMHVWDPELpQSXHGHGHEHUVHDIDFWRUHVGHSROtWLFDHFRQyPLFDUHJXODFLyQGHODRIHUWDPRQHWDULD
(OEDQFR,WDX%%$6$6XFXUVDO8UXJXD\WHQtDHQHOXQGHSRVLWDQWH
2
GH 6LQ HPEDUJR HVWH WLSR GH ULHVJR QR KD VLGR WUDWDGR H[SOtFLWDPHQWH HQ ORV
PRGHORV GH FRUULGDV EDQFDULDV 7DQWR ORV PRGHORV WUDGLFLRQDOHV FRPR ORV GH %U\DQW
'LDPRQG \ '\EYLJ R PiV FHUFDQRV HQ HO WLHPSR FRPR HO GH 5RFKHW9LYHV
QRFRQVLGHUDQHVWHSXQWR(VWRVPRGHORV VXSRQHQ LQGLYLGXRV FRQ XQ PLVPR QLYHO
GH GHSyVLWR LQLFLDO 1R VH DQDOL]D FyPR OD KHWHURJHQHLGDG GH ORV GHSyVLWRV LQLFLDOHV GH
ORVLQGLYLGXRVDIHFWDUtDDORVHTXLOLEULRVGHOPRGHOR
(Q HVH VHQWLGR 0F &DQGOHVV KDFH XQD H[FHSFLyQ (Q HVWH WUDEDMR VH VXSRQH TXH
XQ FRQWLQXR GH DJHQWHV DFW~DQ HQ EORTXH FRPSRUWiQGRVH FRPR VL IXHUD XQ JUDQ
GHSRVLWDQWH6LQHPEDUJRHVWHDUWtFXORDSXQWDSULQFLSDOPHQWHDODIRUPDGHOFRQWUDWR
ySWLPR GH ORV GHSyVLWRV \ D ORV UHTXHULPLHQWRV GH OLTXLGH] \ GH FDSLWDO PiV
FRQYHQLHQWH VLQ FHQWUDU VX DQiOLVLV HQ ORV ULHVJRV TXH SXHGDQ H[LVWLU GHELGR D OD
FRQFHQWUDFLyQ GH ORV GHSyVLWRV (VWD FXHVWLyQ HVWi HQ FLHUWD IRUPD UHODFLRQDGD FRQ HO
Q~PHUR ySWLPR GH DFUHHGRUHV (O WHPD \D KD VLGR HVWXGLDGR SRU %ROWRQ \ 6FKDUIVWHLQ
/DV FRQFOXVLRQHV D OD TXH OOHJDQ VRQ ODV VLJXLHQWHV HO Q~PHUR ySWLPR GH
DFUHHGRUHV
GHSHQGHUtD
GH
OD
SUREDELOLGDG
GH
GHIDXOW
GH
OD
HPSUHVD
OD
FRPSOHPHQWDULHGDG\HOFLFORGHVXVDFWLYRV
1XHVWUR WUDEDMR DQDOL]D HVH SUREOHPD GHVGH XQD ySWLFD GLVWLQWD OD GRPLQDQFLD
HVWRFiVWLFD\VHHQIRFDIXQGDPHQWDOPHQWHHQXQFDVRSDUWLFXODUGHHVWHSUREOHPDTXH
HVODUHODFLyQHQWUHODFRQFHQWUDFLyQGHORVGHSRVLWDQWHV\HOULHVJRGHODGLVWULEXFLyQGH
ORV UHWLURV 1R HVSHFLILFDPRV ORV FRQWUDWRV GH GHXGD ySWLPRV QL FXHVWLRQHV VREUH OD
OLTXLGDFLyQGHVXVDFWLYRVGHUHFKRVGHYRWR
(Q UHVXPHQ HO SURSyVLWR GH HVWH WUDEDMR HV PRVWUDU TXH XQD HVWUXFWXUD GH GHSyVLWRV
FRQFHQWUDGD OOHYD D TXH OD GLVWULEXFLyQ GH ORV UHWLURV EDQFDULRV VHD GH PD\RU ULHVJR (V
SRU HOOR TXH ILMDU HQFDMHV EDQFDULRV VLQ WHQHU HQ FXHQWD OD FRQFHQWUDFLyQ GH ORV
GHSyVLWRVQRSDUHFHDGHFXDGR
(O SUHVHQWH WUDEDMR VH HVWUXFWXUD GH OD VLJXLHQWH IRUPD (Q OD SULPHUD SDUWH GH OD
VLJXLHQWH VHFFLyQ VH SUHVHQWDQ GHILQLFLRQHV \ WHRUHPDV VREUH GRPLQDQFLD HVWRFiVWLFD \
PHGLGDV GH FRQFHQWUDFLyQ GH GRWDFLRQHV (Q OD VHJXQGD SDUWH GH HVD VHFFLyQ VH
4
6L WRGRV ORV GHSRVLWDQWHV UHWLUDUDQ VXV GHSyVLWRV GH DFXHUGR D XQD YDULDEOH %HUQRXOOL LQGHSHQGLHQWHV \ FRQ OD PLVPD
SUREDELOLGDGHQWRQFHVHOSHRUHVFHQDULRTXHVHUHWLUHWRGRHOSDVLYRHVFODUDPHQWHVXSHULRUFRQXQGHSRVLWDQWH
3
GHPXHVWUD XQ WHRUHPD VREUH OD GRPLQDQFLD HVWRFiVWLFD GH VHJXQGR RUGHQ TXH DPSOtD
ORV UHVXOWDGRV SUHVHQWDGRV SRU +DQRFK \ /HY\ +DGDU \5XVVHOO 7HVIDWVLRQ
\/L\:RQJ(QODWHUFHUDVHFFLyQVHDSOLFDHVWHWHRUHPDSDUD UHVROYHU OD
FRQMHWXUD VREUH HO ULHVJR HQ OD FRQFHQWUDFLyQ GH ORV GHSyVLWRV EDQFDULRV /DV
FRQFOXVLRQHVGHHVWHDQiOLVLVVHSUHVHQWDQHQODFXDUWD\~OWLPDVHFFLyQ
&21&(372635(/,0,1$5(6
/DLGHDFHQWUDOHQHOULHVJRGHOLTXLGH]GHELGRDODFRQFHQWUDFLyQGHGHSyVLWRVEDQFDULRV
FRQVLVWHHQPRVWUDUTXHXQDHVWUXFWXUDDWRPL]DGDHVPHQRVULHVJRVDTXHXQDHVWUXFWXUD
FRQFHQWUDGD
GH
GHSyVLWRV
&RQYLHQH
SUHVHQWDU
XQ
HMHPSOR
SDUD
FODULILFDU
OD
DUJXPHQWDFLyQ
6XSRQJDPRVTXHXQEDQFRGHEHHOHJLUHQWUHGRVRSFLRQHVGHILQDQFLDPLHQWRSURYLVWDSRU
WUHV LQGLYLGXRV SRU XQ WRWDO GH XQD XQLGDG PRQHWDULD 6HDQ HVWDV GRV RSFLRQHV
H[SUHVDGDV HQ IRUPD YHFWRULDO \ RUGHQDGDV SRU HO GHSyVLWR TXH KDFH FDGD LQGLYLGXR
1 1 3
1 2 2
z = ( , , ) \ v = ( , , ) (Q OD SULPHUD RSFLyQ SRU HMHPSOR ORV GRV SULPHURV
5 5 5
5 5 5
LQGLYLGXRV GHSRVLWDQ XQ TXLQWR \ HO WHUFHU LQGLYLGXR GHSRVLWD WUHV TXLQWRV 0LHQWUDV TXH
OD VHJXQGD RSFLyQ GLILHUH ~QLFDPHQWH GH OD SULPHUD HQ TXH ORV GRV ~OWLPRV LQGLYLGXRV
GHSRVLWDQGRVTXLQWRV$VXPDPRVTXHFDGDGHSRVLWDQWHUHWLUDODWRWDOLGDGGHVXGHSyVLWR
HQ XQ PRPHQWR GDGR 5HDOL]D HVWH UHWLUR GH DFXHUGR D XQD VHxDO
GLVWULEXFLyQ %HUQRXOOL 6L
X i TXH WLHQH
X i = 1 UHWLUD OD WRWDOLGDG GH VX GHSyVLWR HQ FDVR FRQWUDULR OR
PDQWLHQH 6XSRQJDPRV TXH ODV VHxDOHV HQWUH ORV GHSRVLWDQWHV VRQ LGpQWLFDPHQWH
GLVWULEXLGDV H LQGHSHQGLHQWHV HQWUH Vt 3RU OR WDQWR ORV UHWLURV DJUHJDGRV
x SXHGHQ
H[SUHVDUVHFRPRXQDIXQFLyQGHOYHFWRUGHGHSyVLWRVLQLFLDOHVGHSHQGLHQGRGHODIRUPD
GH ILQDQFLDPLHQWR TXH VH RSWH \ VHUiQ LJXDOHV D 1
1
3
X1 + X 2 + X 3
5
5
5
y
1
2
2
X 1 + X 2 + X 3 UHVSHFWLYDPHQWH
5
5
5
'HPRVSRUVXSXHVWRTXHODIXQFLyQREMHWLYRGHOEDQFRHVGHODIRUPD
XQDIXQFLyQFyQFDYDUHVSHFWRGHORVUHWLURVDJUHJDGRV
π (x) \TXH π
HV
x
(Q7LUROHVHKDFHXQSHTXHxRDQiOLVLVVREUHHVWHWHPD
4
¢&XiO GH ODV GRVHVWUXFWXUDV GH GHSyVLWRV WHQGUi OD GLVWULEXFLyQ GH UHWLURV GH PHQRU
ULHVJR"
(QSULPHUOXJDUGHEHPRVDFODUDUHOFRQFHSWRTXHOHGDPRVDOWpUPLQRULHVJR 7HQHPRV
GRV YDULDEOHV DOHDWRULDV GH UHWLURV DJUHJDGRV FDGD XQD FRQ FLHUWD GLVWULEXFLyQ GH
SUREDELOLGDG\GHEHPRVGHFLUFXiOGHODVGRVWLHQHPD\RUULHVJR([LVWHQYDULRVFULWHULRV
SDUD DQDOL]DU HO ULHVJR HQWUH YDULDEOHV DOHDWRULDV &RPR HVWDV GRV YDULDEOHV WLHQHQ OD
PLVPD PHGLD QR HV SRVLEOH VHJXLU XQ FULWHULR XWLOL]DQGR VRODPHQWH HVWH PRPHQWR
HVWDGtVWLFR 'H KHFKR KDELWXDOPHQWH VH DVRFLD HO ULHVJR GH XQD YDULDEOH DOHDWRULD FRQ
ODGLVSHUVLyQUHVSHFWRGHVXYDORUPHGLR
(VWHHVHOPpWRGRWUDGLFLRQDOTXHVHFRQRFHFRPR´PHDQYDULDQFHDQDO\VLVµ\RSHUDGH
OD VLJXLHQWH IRUPD 6L WHQHPRV SRU HMHPSOR GRV YDULDEOHV DOHDWRULDV FRQ OD PLVPD
PHGLD OD YDULDEOH TXH WXYLHUD PD\RU YDULDQ]D VHUtD OD PiV ULHVJRVD (VWH PpWRGR WLHQH
YDULDV YHQWDMDV 8QD GH HOODV HV OD VHQFLOOH] SDUD RUGHQDU IXQFLRQHV GH YDULDEOHV
DOHDWRULDV 6LQ HPEDUJR HV FULWLFDGR HQWUH RWUDV FRVDV SRU OD LQFRQVLVWHQFLD HQ VX
RUGHQDPLHQWR
&RPR VH VXJLHUH HQ 5RWVFKLOG \ 6WLJOLW] XQ PpWRGR PiV DSURSLDGR GH
RUGHQDPLHQWR GHO ULHVJR HV OD OODPDGD GRPLQDQFLD HVWRFiVWLFD GH VHJXQGR RUGHQ $
GLIHUHQFLD GHO DQWHULRU OD SULQFLSDO YHQWDMD GH HVWH PpWRGR HV OD FRQVLVWHQFLD HQ VX
RUGHQDPLHQWR3HURWLHQHYDULDVGHVYHQWDMDV8QDGHHOODVFRPRYHUHPRVPiVDGHODQWH
HV OD GLILFXOWDG GH RUGHQDU IXQFLRQHV GH GLYHUVDV YDULDEOHV DOHDWRULDV 1R REVWDQWH
GHELGR D VX FRQVLVWHQFLD XWLOL]DUHPRV HVWH ~OWLPR PpWRGR SDUD GHWHUPLQDU HO ULHVJR GH
XQD YDULDEOH DOHDWRULD (Q OD VLJXLHQWH VHFFLyQ VH SUHVHQWDQ GHILQLFLRQHV \ SURSLHGDGHV
EiVLFDV TXH QRV SHUPLWLUiQ UHVSRQGHU FXiO GH ODV GRV HVWUXFWXUD GH GHSyVLWRV HV PiV
ULHVJRVD
/D SULQFLSDOFUtWLFDHV TXH HO RUGHQDPLHQWRPHGLDQWH HO PHDQ YDULDQFH DQDO\VLV \ HO TXH KDUtDXQ LQGLYLGXR DYHUVR DO
ULHVJRQRVRQHTXLYDOHQWHV
5
'(),1,&,21(6<3523,('$'(6%$6,&$6
'HILQLFLyQGHOD'RPLQDQFLDHVWRFiVWLFDGHVHJXQGRRUGHQ
6HDQ
X
H
Y GRVYDULDEOHVDOHDWRULDVFRQIXQFLRQHVGHGLVWULEXFLyQDFXPXODGDV F \ G
UHVSHFWLYDPHQWH FDGD XQD FRQ VRSRUWH HQ
(VWR HV
1
1
0
0
∫ xdF ( x) = ∫ xdG( x) < ∞
RUGHQ D
Y
s
s
0
0
[0,1] \ DGHPiV FRQ OD PLVPD PHGLD ILQLWD
'HFLPRV TXH
X
GRPLQD HVWRFiVWLFDPHQWH GH VHJXQGR
\ OR H[SUHVDUHPRV FRQ HO VtPEROR 2
X
2
Y
VL \ VROR VL
∫ G ( x)dx ≥ ∫ F ( x)dx ∀s ∈ [0,1]
3URSLHGDGHVGHODGRPLQDQFLDHVWRFiVWLFDGHVHJXQGRRUGHQ
$OJXQDV SURSLHGDGHV GH OD GRPLQDQFLD HVWRFiVWLFD TXH VHUiQ GH XWLOLGDG PiV DGHODQWH
VRQODVVLJXLHQWHV
D(Q5RWVFKLOG\6WLJOLW]VHGHPXHVWUDTXHHVHTXLYDOHQWHSUREDUTXH
HVWRFiVWLFDPHQWH GH VHJXQGR RUGHQ D
HQOXJDUGH
F
X
Y D TXH XQ LQGLYLGXR DYHUVR DO ULHVJR
GRPLQD
HOLJH
X
Y
G VL\VRORVL E f (u ) ≥ E g (u ) VLHQGR u XQDIXQFLyQFyQFDYD 2
E$GHPiVSRUWHQHU
1
1
s
s
X
H
Y ODPLVPDPHGLD\SRU X
2
Y HQWRQFHVVHFXPSOHTXH
∫ F ( x)dx ≥ ∫ G ( x)dx ∀s ∈ [0,1]
/DGRPLQDQFLDHVWRFiVWLFDGHVHJXQGRRUGHQQRVPXHVWUDTXHODSHUIHFWDGLYHUVLILFDFLyQ
HV SUHIHULGD SRU LQGLYLGXRV DYHUVRV DO ULHVJR (Q ORV DUWtFXORV GH +DQRFK \ /HY\ +DGDU\5XVVHOO7HVIDWVLRQ*ROOLHU\/L\:RQJ VH SUHVHQWDQ
\GHPXHVWUDQHVWDDILUPDFLyQHQHOVLJXLHQWHWHRUHPD
(VWHSXQWRHVLPSRUWDQWHSDUDUHVSRQGHUODSUHJXQWDGHOHMHPSORSODQWHDGRSXHVDOVHUODIXQFLyQGHOEDQFRFyQFDYDHO
EDQFRHOHJLUiODGLVWULEXFLyQGHUHWLURVGHPHQRUULHVJR
(QHVWHWUDEDMR
f
\
g VHUiQUHVSHFWLYDPHQWHODVIXQFLRQHVGHGHQVLGDGGH F \ G 6
7HRUHPD
6HDQ
X 1 , X 2 ,..., X n YDULDEOHV DOHDWRULDV LQGHSHQGLHQWHV H LGpQWLFDPHQWH GLVWULEXLGDV \
n
VHDXQYHFWRU
α SHUWHQHFLHQWHD R+n FRQ 0 ≤ α i ≤ 1 \ ∑ α i = 1 HQWRQFHV
1
n
∑
1
Xi
n
n
2
∑α
i
Xi
2
X i SDUDWRGR i = 1,2,..., n
1
'HPRVWUDFLyQ
9pDVHSURSRVLFLyQGH*ROOLHURWHRUHPDGH/L\:RQJ
1yWHVHTXHHOWHRUHPDDQWHULRUVHOLPLWD~QLFDPHQWHDFRPSDUDUFRPELQDFLRQHVOLQHDOHV
HQWUH OD SHUIHFWD GLYHUVLILFDFLyQ \ FXDOTXLHU RWUD FRPELQDFLyQ OLQHDO FRQYH[D GH
YDULDEOHV DOHDWRULDV R HQWUH HVWDV ~OWLPDV \ YDULDEOHV DOHDWRULDV LQGLYLGXDOHV 1XHVWUR
SURSyVLWR HV DYDQ]DU XQ SRFR PiV \ SRGHU FRPSDUDU OD GRPLQDQFLD HVWRFiVWLFD GH
VHJXQGRRUGHQHQWUHFRPELQDFLRQHVOLQHDOHVFRQYH[DVGHYDULDEOHVDOHDWRULDVORFXDOQR
HVSRVLEOHKDFHUFRQHOWHRUHPD
/D SHUFHSFLyQ LQGLFDUtD TXH XQD FRPELQDFLyQ PHQRV GHVLJXDO GH YDULDEOHV DOHDWRULDV
VHUtDSUHIHULGDSRUXQDJHQWHDYHUVRDOULHVJRDXQDFRPELQDFLyQPiVFRQFHQWUDGD
¢&yPRPHGLPRVODFRQFHQWUDFLyQ"
'HEHPRV GHILQLU XQ FULWHULR SDUD FRPSDUDU OD FRQFHQWUDFLyQ HQWUH YHFWRUHV GH Q~PHURV
UHDOHV ([LVWHQ YDULRV tQGLFHV GH PHGLFLyQ GH OD FRQFHQWUDFLyQ /LPLWDUHPRV QXHVWUR
DQiOLVLV D WUHV GH ORV PiV XVDGRV TXH VRQ HO tQGLFH GH +HUILQGDKO+LUVFKPDQQ HO
tQGLFH GH *LQL \ HO RUGHQ GH /RUHQ] 'HILQLUHPRV HVWRV PpWRGRV SDUD GRV YHFWRUHV
y SHUWHQHFLHQWHV D R+n RUGHQDGRV GH OD VLJXLHQWH IRUPD
x H
0 ≤ x1 ≤ x 2 ≤ ... ≤ x n ≤ 1 \
0 ≤ y1 ≤ y 2 ≤ ... ≤ y n ≤ 1 6LHQGR SDUD FDGD YHFWRU xi y i OD GRWDFLyQ GHO LQGLYLGXR i $GHPiVVXSRQHPRVTXH
D
n
n
1
1
∑ x i = ∑ y i = 1 'HFLPRV TXH HO YHFWRU
x GRPLQD DO YHFWRU y WLHQH PHQRU R LJXDO tQGLFH GH
+HUILQGDKO+LUVFKPDQQ++
\ORH[SUHVDPRV
(ODUWLFXORGH6DPXHOVRQHVSLRQHURHQHVWHWHPD
(QWRGRVORVFDVRVHOYHFWRUGRPLQDQWHHVHOPHQRVFRQFHQWUDGR
7
x
E
HH
n
n
1
1
y VL\VRORVLVHFXPSOHTXH ∑ x i2 ≤ ∑ y i2
'HFLPRVTXHHOYHFWRU
x GRPLQDDOYHFWRU y WLHQHPHQRURLJXDOtQGLFHGH*LQL\
n
ORH[SUHVDPRVGHODVLJXLHQWHIRUPDUHFRUGDQGRTXHVXSXVLPRV
n
∑x =∑y
i
1
x
F
IG
y VL\VRORVL
'HFLPRVTXHHOYHFWRU
L
= 1
n
n
1
1
(n + 1 − 2∑ (n + 1 − i ) x i ) ≤ (n + 1 − 2∑ (n + 1 − i ) y i )
n
n
i =1
i =1
x /RUHQ]GRPLQDDOYHFWRU y \ORH[SUHVDPRV
k
x
i
1
k
y VL\VRORVLVHFXPSOHTXH ∑ x i ≥ ∑ y i
1
FRQ
k = 1,2,..., n 1
(O RUGHQ GH /RUHQ] FXPSOH FRQ FLHUWDV SURSLHGDGHV TXH SUHVHQWDPRV D FRQWLQXDFLyQ \
TXHVHUiQGHXWLOLGDGPiVDGHODQWH
'HILQLFLyQ7UDQVIHUHQFLDGH'DOWRQ3LJRX
'HFLPRV TXH H[SUHVD
x VH REWLHQH GH y PHGLDQWH XQD ~QLFD WUDQVIHUHQFLD GH 'DOWRQ \ VH
x v D y 6LSRGHPRVREWHQHUDOYHFWRU x DSDUWLUGHOYHFWRU y PHGLDQWHXQD
WUDQVIHUHQFLD GH XQ LQGLYLGXR PiV ULFR D RWUR PiV SREUH WUDQVILULHQGR XQD VXPD WDO TXH VH FXPSOD (
ε >0
xi = yi + ε \ x j = y j − ε FRQ y k x k k p i, j SDUD DOJXQRV
y i y j FRQ ε ∈ 0, ( y j − yi )
2
)
(Q HVWH VHQWLGR VH GLFH TXH OD GRWDFLyQ
x HV PHQRV GHVLJXDO TXH OD GRWDFLyQ y SXHV
GLILHUHQHQWUHVtHQTXHXQLQGLYLGXRPiVULFROHWUDQVILHUHSDUWHGHVXGRWDFLyQDXQ
LQGLYLGXR PiV SREUH PDQWHQLpQGRVH HO PLVPR RUGHQ LQLFLDO HQWUH ORV LQGLYLGXRV 6L
DSOLFDPRVHVWRVWUDVSDVRVHQIRUPDLWHUDWLYDSRGUHPRVREWHQHUVXFHVLYDVWUDQVIHUHQFLDV
ILQLWDV HQWUH ORV YHFWRUHV TXH SHUPLWHQ REWHQHU RWUD IRUPD GH RUGHQDPLHQWR (VWR VH
FRQRFHFRPRRUGHQGH'DOWRQ3LJRX
6LORVYHFWRUHVFXPSOHQHVWDSURSLHGDGVHGLFHTXH
x PD\RUL]DD y YHU0DUVKDOO\2ONLQ6HGLFHWDPELpQTXH
HVWRVGRVYHFWRUHVVRQFRPSDUDEOHV
8
'HILQLFLyQGHORUGHQGH'DOWRQ3LJRX
6H GHILQH XQ RUGHQ GH 'DOWRQ \ VH H[SUHVD FRPR
VROR VL H[LVWH XQ Q~PHUR ILQLWR GH YHFWRUHV
TXH
x
D
y x 'DOWRQ GRPLQD D y VL \
y 0 , y 1 , . . . , y m SHUWHQHFLHQWHV D Rn WDO
x ym v D . . vD y0 y /RV PpWRGRV GH /RUHQ] \ 'DOWRQ 3LJRX SUHVHQWDQ GRV PHGLGDV SDUD RUGHQDU YHFWRUHV
VHJ~Q VX GHVLJXDOGDG ,QPHGLDWDPHQWH VXUJH OD SUHJXQWD GH VL HVWRV GRV PpWRGRV HVWiQ
UHODFLRQDGRVGHDOJXQDIRUPD/DUHVSXHVWDHVTXHVtH[LVWHXQDUHODFLyQHVWUHFKDHQWUH
HORUGHQGH/RUHQ]\HORUGHQGH'DOWRQ3LJRX\ORH[SUHVDPRVHQHOVLJXLHQWHWHRUHPD
7HRUHPD
(OYHFWRU
x /RUHQ]GRPLQDDOYHFWRU y VL\VRORVL x 'DOWRQGRPLQDD y 'HPRVWUDFLyQ
9HUWHRUHPD,,GH5RVWVFKLOG\6WLJOLW]
([LVWH XQD UHODFLyQ GLUHFWD HQWUH HO RUGHQ GH /RUHQ] \ ORV RWURV GRV tQGLFHV (Q HO
VLJXLHQWH WHRUHPD PRVWUDUHPRV TXH VL HO YHFWRU
HQWRQFHVHOYHFWRU
x /RUHQ] GRPLQD DO YHFWRU y x GRPLQDVHJ~Q+HUILQGDKO+LUVFKPDQQDOYHFWRU y 7HRUHPD
6L
n
n
1
1
y HQWRQFHV ∑ x i2 ≤ ∑ y i2
L
x
'HPRVWUDFLyQ
&RPR
x
k
k
1
1
y ⇒ ∑ x i ≥ ∑ y i ∀k = 1,2,..., n 0XOWLSOLFDQGROD~OWLPDH[SUHVLyQHQDPERV
L
ODGRVSRU
k
k
1
1
( x k − x k +1 ) REWHQHPRV ( x k − x k +1 )∑ x i ≤ ( x k − x k +1 )∑ y i ∀k = 1,2,..., n 6XPDQGRHQDPERVODGRVGH
k = 1 KDVWD k = n \VDELHQGRTXH x n +1 = 0 REWHQHPRV
(OQ~PHURGHWUDQVIHUHQFLDVVHUiPHQRURLJXDODQ
9
n
n
∑ x i2 ≤ ∑ xi y i
1
3RU OD GHVLJXDOGDG GH 6FKZDUW] VH FXPSOH 1
2
n
HQWRQFHV
n
n
n
n
n
1
1
1
1
1
n
n
n
1
1
1
(∑ x i y i ) 2 ≤ ∑ x i2 ∑ y i2
(∑ x ) ≤ (∑ x i y i ) 2 ≤ ∑ x i2 ∑ y i2 ⇒ ∑ x i2 ≤ ∑ y12 2
i
1
4('
7DPELpQ ORV YHFWRUHV RUGHQDGRV TXH VRQ RUGHQDGRV SRU HO FULWHULR GH /RUHQ] OR VRQ
XWLOL]DQGRHOtQGLFHGHFRQFHQWUDFLyQGH*LQL
7HRUHPD
6L
x
L
y HQWRQFHV x
IG
y
'HPRVWUDFLyQ
6L
x
IG
y HQWRQFHV
n
n
1
1
(n + 1 − 2∑ (n + 1 − i ) x i ) ≤ (n + 1 − 2∑ (n + 1 − i ) y i )
n
n
i =1
i =1
2SHUDQGR\VLPSOLILFDQGRREWHQHPRVTXH
n
n
n
n
1
1
(
n
1
i
)
x
)
(n + 1 − i) y i ) ≤
⇔
+
−
≥
(n + 1 − 2∑ (n + 1 − i) y i )
(n + 1 − 2∑ (n + 1 − i ) x i )
∑
∑
i
n
n
i =1
i =1
i =1
i =1
&RPR
x
k
k
1
1
y ⇒ ∑ xi ≥ ∑ yi
L
6HFXPSOHSDUDFDGDYDORUGH
FRQ
k = 1,2,..., n k
k = 1 x1 ≥ y 2 k = 2 x1 + x 2 ≥ y1 + y 2
k = n x1 + x 2 + ... + x n = y1 + y 2 + ... + y n 6XPDQGR WRGDV HVWDV GHVLJXDOGDGHV GH
n
EXVFDGD
KDVWD
k = n REWHQHPRV OD UHODFLyQ
n
∑ (n + 1 − i) x ) ≥ ∑ (n + 1 − i) y )
i
i =1
k =1
i
4('
i =1
10
'HEHPRV QRWDU TXH HO UHFtSURFR GH DPERV WHRUHPDV QR VH FXPSOH 6L HOHJLPRV ORV
YHFWRUHV 1 1
1 3 8
a = (0, , ) b = ( , , ) VDEHPRV TXH VH FXPSOH a
2 2
12 12 12
3HURORVYHFWRUHV
FDPELD D
a \ b QRVRQ/RUHQ]FRPSDUDEOHVSXHV 0 <
HH
b \ a
IG
b
1
\OXHJRODGHVLJXDOGDG
2
1 4
> (OOR VH GHEH D TXH HO RUGHQ GH /RUHQ] HV LQFRPSOHWR SDUD YHFWRUHV
2 12
GH GLPHQVLyQ PD\RUHV D GRV 1RWHPRV DGHPiV DXQTXH ORV YHFWRUHV VH SXHGHQ RUGHUDU
WDQWRSRUHOtQGLFHGH*LQLFRPRSRUHOGH++QRVRQ/RUHQ]FRPSDUDEOHV1yWHVHTXH
SRUORVGRVWHRUHPDVDQWHULRUHVQXQFDSRGUtDUHYHUWLUVHVXFODVLILFDFLyQ
(;7(16,21'(/$'20,1$1&,$(672&$67,&$3$5$9$5,$%/(6$/($725,$6
/RVDUWtFXORVSLRQHURVGH+DQRFN\/HY\+DGDU\5XVVHOO5RWVFKLOG
\ 6WLJOLW] \ 7HVIDWVLRQ GHPXHVWUDQ WHRUHPDV GH GRPLQDQFLD HVWRFiVWLFD
SULQFLSDOPHQWH SDUD IXQFLRQHV GH GRV YDULDEOHV DOHDWRULDV (O WUDEDMR GH /L \ :RQJ
H[WLHQGH HVWRV WHRUHPDV SDUD IXQFLRQHV GH
n YDULDEOHV DOHDWRULDV 1R REVWDQWH
D SHVDU GH HVWRV DYDQFHV GLFKRV DUWtFXORV VRQ D~Q LQVXILFLHQWHV SDUD FRQWHVWDU OD
FRQMHWXUD VREUH HO ULHVJR SRU OD FRQFHQWUDFLyQ GH ORV YHFWRUHV (O PRWLYR HV TXH HVWRV
WHRUHPDV QR QRV SHUPLWHQ FRPSDUDU OD GRPLQDQFLD HVWRFiVWLFD GH VHJXQGR RUGHQ HQWUH
FRPELQDFLRQHV OLQHDOHV FRQYH[DV GH YDULDEOHV DOHDWRULDV 'HEHPRV UHPLWLUQRV SXHV DO
WUDEDMR GH 0DUVKDOO \ 3URVFKDQ SDUD ORJUDU VDOYDU HVWD IDOHQFLD 6LQ HPEDUJR HQ
HVH WUDEDMR QR VH LQWHUSUHWD HO UHVXOWDGR FRPR XQ RUGHQDPLHQWR GH GRPLQDQFLD
HVWRFiVWLFD GH VHJXQGR RUGHQ 7DPSRFR PXHVWUD OD YLQFXODFLyQ HQWUH OD GRPLQDQFLD
HVWRFiVWLFD \ OD FRQFHQWUDFLyQ GH ORV YHFWRUHV 3RU HOOR SUHVHQWDUHPRV XQ WHRUHPD TXH
PXHVWUD HO YtQFXOR GLUHFWR TXH H[LVWH HQWUH OD FRQFHQWUDFLyQ \ OD GRPLQDQFLD
HVWRFiVWLFD $ GLIHUHQFLD GHO WUDEDMR GH 0DUVKDOO \ 3URVFKDQ XWLOL]DUHPRV ORV
DUWtFXORVGH+DGDU\5XVVHOO7HVIDWVLRQ\/L\:RQJSDUDKDFHUVX
SUXHED$FRQWLQXDFLyQSUHVHQWDUHPRVDOJXQRVWHRUHPDVQHFHVDULRVSDUDHVWHSURSyVLWR
11
7HRUHPD
6HDQ
X
\
Y GRV YDULDEOHV DOHDWRULDV LQGHSHQGLHQWHV H LGpQWLFDPHQWH GLVWULEXLGDV 6HD
W XQD YDULDEOH DOHDWRULD LQGHSHQGLHQWH GH X
\ GH
a, b ∈ R FRQ a > 0 \ b ≥ 0 VHFXPSOHTXH aX + bW
2
Y 6L X
2
Y HQWRQFHV SDUD
aY + bW
'HPRVWUDFLyQ
9pDVHWHRUHPD
HQ7HVIDWVLRQ
7HRUHPD
6HDQ ^
Z 1 .Z 2 ,...Z n ` XQ FRQMXQWR GH YDULDEOHV DOHDWRULDV LQGHSHQGLHQWHV \ ^ W1 , W2 ,..., Wn }
RWURFRQMXQWRGHYDULDEOHVLQGHSHQGLHQWHV
n
Zi
2 Wi ∀i = 1, 2,..., n VL\VRORVL ∑ θ i Z i
1
n
2
∑θ W
i
i
∀θ i ≥ 0 SDUDWRGR i = 1,2,..., n
1
'HPRVWUDFLyQ
9pDVH7HRUHPDGH/L\:RQJ
1XHVWURSURSyVLWRHVWHQHUXQPpWRGRTXHQRVSHUPLWDFRPSDUDUFRPELQDFLRQHVOLQHDOHV
FRQYH[DV FX\RV YHFWRUHV GH FRHILFLHQWHV WHQJDQ GLVWLQWD FRQFHQWUDFLyQ (Q OD VHFFLyQ
DQWHULRU
YLPRV
WUHV
PpWRGRV
SDUD
FODVLILFDU
YHFWRUHV
VHJ~Q
VX
FRQFHQWUDFLyQ
0RVWUDUHPRV PiV DGHODQWH TXH HO ~QLFR PpWRGR TXH SHUPLWH FRPSDUDU OD GRPLQDQFLD
HVWRFiVWLFDGHVHJXQGRRUGHQHQIRUPDJHQHUDOHQWUHFRPELQDFLRQHVOLQHDOHVFRQYH[DV
GH YDULDEOHV DOHDWRULDV HV HO RUGHQ GH /RUHQ] (V SRU HVWR TXH HQXQFLDUHPRV HVWH
WHRUHPD XWLOL]DQGR HVWH PpWRGR GH FRQFHQWUDFLyQ /XHJR PRVWUDUHPRV TXH HO WHRUHPD
QRVHFXPSOHVLVHXWLOL]DQORVLQGLFDGRUHVGH++\HOGH*LQL
7HRUHPD
6HDQ
VHDQ X 1 , X 2 ,..., X n YDULDEOHV DOHDWRULDV LQGHSHQGLHQWHV H LGpQWLFDPHQWH GLVWULEXLGDV \
) \ * GRV YHFWRUHV SHUWHQHFLHQWHV D Rn \ RUGHQDGRV HQ IRUPD FUHFLHQWH
n
n
1
1
0 ≤ α1 ≤ α 2 ≤ ... ≤ α n ≤ 1 0 ≤ β 1 ≤ β 2 ≤ ... ≤ β n ≤ 1 FRQ ∑ α i = ∑ β i = 1 12
6L
α
L
β
n
HQWRQFHV
n
∑α i X i
2
1
'HPRVWUDFLyQ
∑β
i
Xi
1
6HGHPRVWUDUiHQGRVHWDSDV
3DVR
6XSRQJDPRV TXH WHQHPRV GRV YHFWRUHV +
\ 2
SHUWHQHFLHQWHV D Rn FRQ
+ +1 , . . . , + i , . . . +j , . . . , +n RUGHQDGR HQ IRUPD FUHFLHQWH 0 t +1 t. . . t +n t 1 \
θ = (θ1 ,θ 2 ,...,θ n ) = (γ 1 , γ 2 ,..., γ i + ε ,...., γ j − ε ,..., γ n ) FRQ γ j −γ i
ε ∈ 0,
2
&RPR VH YH HVWR HV OD
GHILQLFLyQGHXQDWUDQVIHUHQFLDGH'DOWRQ\ODH[SUHVDPRVFRPR
n
/ODPDQGR D W = ∑θ i X i
n
\ 1
W
2
Z
2 v D + Z = ∑ γ i X GHPRVWUDUHPRV TXH VL θ → D γ
HQWRQFHV
1
'HPRVWUDFLyQSDVR
2EVHUYHPRV TXH SDUD GRV YDULDEOHV DOHDWRULDV LQGHSHQGLHQWHV H LGpQWLFDPHQWH
GLVWULEXLGDV
X i \ X j VHFXPSOHTXH
(γ i + ε ) X i + (γ j − ε ) X j
2
γ i X i + γ j X j (QSULPHUOXJDUH[SUHVHPRVFRQQRWDFLyQPiVVHQFLOODSDUDHOORPXOWLSOLTXHPRVHQ
DPERV ODGRV GH SRU
\
βj =
γ
j
γi +γ
1
γ i +γ j
\ OODPHPRV D
αi =
γi +ε
γi +γ j
αj =
γi −ε
γi +γ j
βi =
γi
γi +γ
j
&RQHVWDQXHYDQRWDFLyQSUREDUHVHTXLYDOHQWHDPRVWUDUTXH
j
(VWHWHRUHPDSXHGHGHPRVWUDUVHXVDQGRHOFRQFHSWRGHFRQYH[LGDGGH6FKXU9HU0DUVKDOO\3URVFKDQR0DUVKDOO\2ONLQ
1RREVWDQWHFRPRGLMLPRVSUHIHULPRVUHDOL]DUXQDGHPRVWUDFLyQPiVHQOtQHDFRQORVWUDEDMRVGH7HVIDWVLRQ\/L\:RQJ
13
αi X i + α j X j
2
β i X i + β j X j (V IiFLO GHPRVWUDU TXH HVWR VH FXPSOH 6L α i = α j =
QRVUHPLWLPRVDOWHRUHPD$VXPLHQGRHQWRQFHVTXH
IRUPDHOUHVXOWDGRHVWULYLDO
'DGDXQDIXQFLyQ
[
1
2
α i < α j \TXH α i > β i GHRWUD
u : R → R FyQFDYDGHEHPRVSUREDUTXH
]
[
E u (α i X i + α j X j ) ≥ E u ( β i X i + β j X j )
]
1yWHVHTXHSRGHPRVH[SUHVDU
α i X i + α j X j = a ( β i X i + β j X j ) + (1 − a ) 12 ( X i + X j )
FRQ
a ∈ (0,1)
6HFXPSOHSXHVTXH
[
E u (α i X i + α j X j )
]
E [u ( a ( β i X i + β j X j ) + (1 − a )
\SRUFRQFDYLGDGGHODIXQFLyQ
[
]
1
( X i + X j ))
2
]
u
[
E u (α 1 X i + α 2 X j ) ≥ E au ( β i X i + β j X j ) + (1 − a ) u(
Xi + X j
2
)
]
$GHPiVSRUHOWHRUHPD
[
E au ( β i X i + β j X j ) + (1 − a ) u(
Xi + X j
2
[
) ] ≥ E au ( β i X i + β j X j ) + (1 − a )u ( β i X i + β j X j )
]
SRUORFXDOVHFXPSOHTXH
[
]
[
E u (α i X i + α j X j ) ≥ E u ( β i X i + β j X j )
]
\SRUORWDQWRVHFXPSOH
14
3XHVXQDPLVPDGLVWULEXFLyQVHGRPLQDHVWRFiVWLFDPHQWHGHVHJXQGRRUGHQDVtPLVPD
14
&RPR ~OWLPR SXQWR SDUD OD GHPRVWUDFLyQ GH HVWH SULPHU SDVR VDEHPRV TXH SRU ORV
WHRUHPDV \ DO VHU ODV YDULDEOHV DOHDWRULDV GH
X 1 , X 2 , . . . , X n LLG HQWRQFHV OD
DGLFLyQGHYDULDEOHVDOHDWRULDVQRFDPELDODGRPLQDQFLDHVWRFiVWLFD
6XPDQGRHQDPERVODGRVGHORV
n " 2 HOHPHQWRVUHVWDQWHV
γ 1 X 1 , γ 2 X 2 ,..., γ i −1 X i −1 , γ i +1 X i +1 ,...., γ
j −1
X j −1 , γ
j +1
X j +1 ,...,., γ n X n VHPDQWLHQHODGRPLQDQFLDHVWRFiVWLFDFRQORFXDOVHFXPSOH
W
2
Z.
3DVR
$KRUDSRUWHRUHPD
α
β ⇒ α
L
D
β
(VWRHVH[LVWHXQDVHFXHQFLDILQLWDGHYHFWRUHV
TXH
(α , χ ,.., η , β ) SHUWHQHFLHQWHVD Rn WDO
α → D χ → D ,.. → D η → D β . (VWROOHYDTXHSRUSDVRXQR
n
∑αi X i
1
n
2
∑ χi X i
1
n
2
...
2
∑ηi X i
1
n
2
∑ βi X i
1
n
\SRUWUDQVLWLYLGDGGHGRPLQDQFLDHVWRFiVWLFDVHFXPSOHTXH
∑αi Xi
1
n
2 ∑βi Xi
1
4('
(VWH WHRUHPD SHUPLWH RUGHQDU OD GRPLQDQFLD HVWRFiVWLFD GH VHJXQGR RUGHQ HQWUH
FRPELQDFLRQHVOLQHDOHVFRQYH[DVGHYDULDEOHVDOHDWRULDVLQGHSHQGLHQWHVHLGpQWLFDPHQWH
GLVWULEXLGDV
15
¢4XpRFXUUHFRQORVRWURVtQGLFHVGHFRQFHQWUDFLyQ"
'H KDEHU XWLOL]DGR ORV RWURV GRV LQGLFDGRUHV GH FRQFHQWUDFLyQ HVWH WHRUHPD QR VH
FXPSOH HQ IRUPD JHQHUDO 3DUD GHPRVWUDU HVWH SXQWR QRV YDOGUHPRV GH XQ HMHPSOR
XWLOL]DQGRORVYHFWRUHVDQWHULRUHV
1 1
1 3 8
a = (0, , ) b = ( , , ) 2 2
12 12 12
1yWHVH TXH WDQWR SDUD ORV tQGLFHV GH ++ \ GH *LQL HO YHFWRU
a
HH
b \ a
IG
a GRPLQD DO YHFWRU b b 'HPRVWUDUHPRVSRUUHGXFFLyQDODEVXUGRTXHHOWHRUHPDDQWHULRU
HVIDOVRGHDSOLFDUVHFRPRPHGLGDGHFRQFHQWUDFLyQFXDOTXLHUDGHHVWRVtQGLFHV
6XSRQJDPRV TXH HO WHRUHPD IXHUD FLHUWR SRU OR WDQWR DPERV tQGLFHV PH KXELHUDQ
n
LQGLFDGRTXH
∑ ai X i
1
n
2
∑b X
i
i SHURGHPRVWUDUHPRVTXHHVWRQRHVFLHUWR
1
7HRUHPD
n
6L
a
HH
b HQWRQFHVQRSRGHPRVDILUPDUTXH ∑ a i X i
1
n
2
∑b X
n
6L
a
IG
b HQWRQFHVQRSRGHPRVDILUPDUTXH ∑ a i X i
1
i
i 1
n
2
∑b X
i
i 1
'HPRVWUDFLyQ
0RVWUDUHPRVFRQXQHMHPSORTXHHOWHRUHPDHVYHUGDGHUR5HIRUPXODQGRHVWDH[SUHVLyQ
FRQORVYHUGDGHURVYDORUHVGH
a
IG
a \ b XWLOL]DGRVDQWHULRUPHQWHVDEHPRVTXH a
HH
b \
b REWHQHPRV
1
1
X 2 + X 3 \ 1 X 1 + 3 X 2 + 8 X 3
2
2
12
12
12
6L SRU HMHPSOR ODV YDULDEOHV
X i WXYLHUDQ GLVWULEXFLyQ %HUQRXOOL \ DGHPiV IXHUDQ
LQGHSHQGLHQWHV 'HILQLHQGR D
P( X i = 0) = p HQWRQFHV OD IXQFLyQ GH GLVWULEXFLyQ
16
DFXPXODGD GH
1
1
2
X 2 + X 3 HQ HO YDORU FHUR VHUtD p PLHQWUDV TXH OD GLVWULEXFLyQ
2
2
DFXPXODGD GH
1
3
8
X1 +
X2 +
X 3 12
12
12
HQ FHUR VHUtD
p 3 3RU GHILQLFLyQ GH GRPLQDQFLD
HVWRFiVWLFD GH VHJXQGR RUGHQ OD IXQFLyQ GH GLVWULEXFLyQ DFXPXODGD GRPLQDQWH SDUD HO
YDORU PtQLPR GHO LQWHUYDOR GH VRSRUWH QR SXHGH VHU PHQRU HVWULFWR D OD GLVWULEXFLyQ
DFXPXODGD GRPLQDGD (Q QXHVWUR FDVR SDUD
FHUR
p ∈ (0,1) HVWR QR RFXUUH 3XHV HQ HO YDORU
p 3 < p 2 \ SRU WDQWR QR SRGHPRV DILUPDU GH IRUPD JHQHUDO TXH
n
∑a X
i
i
2
1
n
∑b X
i
i 4('
1
6HPXHVWUDTXHHOYHFWRUGHFRHILFLHQWHVGHODFRPELQDFLyQOLQHDOGHYDULDEOHVDOHDWRULDV
GRPLQDQWH QXQFD SXHGH WHQHU PHQRV HOHPHQWRV GLVWLQWRV GH FHUR TXH HO YHFWRU GH OD
FRPELQDFLyQGRPLQDGD'HORVWUHVLQGLFDGRUHVHO~QLFRTXHFXPSOHFRQHVWDFRQGLFLyQ
HVHORUGHQGH/RUHQ]
(Q UHVXPHQ HO WHRUHPD SHUPLWH RUGHQDU OD GRPLQDQFLD HVWRFiVWLFD GH VHJXQGR
RUGHQ HQWUH FRPELQDFLRQHV OLQHDOHV FRQYH[DV GH YDULDEOHV DOHDWRULDV LQGHSHQGLHQWHV H
LGpQWLFDPHQWHGLVWULEXLGDV$GHPiVVHPRVWUyTXHHOLQGLFDGRUGHFRQFHQWUDFLyQTXHHV
FRQVLVWHQWH FRQ OD RUGHQDFLyQ TXH KDUtD XQ LQGLYLGXR DYHUVR DO ULHVJR HV HO RUGHQ GH
/RUHQ]
81$$3/,&$&,Ð1$/5,(6*2'(/265(7,526%$1&$5,26
(Q HVWD VHFFLyQ UHDOL]DUHPRV XQD DSOLFDFLyQ GHO WHRUHPD \ PRVWUDUHPRV TXH XQD
HVWUXFWXUD FRQFHQWUDGD GH GHSyVLWRV OOHYD D TXH OD GLVWULEXFLyQ GH ORV UHWLURV EDQFDULRV
WHQJD PD\RU ULHVJR (O LQFUHPHQWR HQ HO ULHVJR RSHUDUtD GH OD VLJXLHQWH IRUPD
6XSRQJDPRVXQEDQFRTXHWLHQHGHSyVLWRVPX\FRQFHQWUDGRVGLJDPRVXQFDVRH[WUHPR
TXH WXYLHUD XQ VROR GHSRVLWDQWH (VH ~QLFR GHSRVLWDQWH SXHGH UHFLELU XQ VKRFN
LQHVSHUDGR GH OLTXLGH] \ H[LJLU OD GHYROXFLyQ WRWDO GHO SDVLYR EDQFDULR 3DUHFH PHQRV
17
SUREDEOHFRQWDOQLYHOGHJUDYHGDGTXHDQWHHOPLVPRVKRFNGHOLTXLGH]HOORRFXUUDHQ
XQDVLWXDFLyQGHDWRPL]DFLyQGHORVGHSyVLWRV
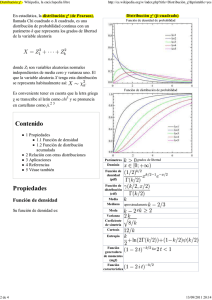
6LREVHUYDPRVHOVLJXLHQWHJUiILFRVHDSUHFLDTXHODEDQFDSULYDGDGH8UXJXD\DO
WHQtDXQDHVWUXFWXUDGHILQDQFLDPLHQWRPX\FRQFHQWUDGD
Depósitos Acum ulados de los depósitos del SNF al 3/2004
Banca Privada
120%
100%
80%
60%
40%
20%
0%
85%
93%
98%
100%
P orcentaje de Depos itantes Acumulado
)XHQWH(ODERUDFLyQSURSLDHQEDVHDGDWRVGHO%&8\7HD'HORLWWH\7RXFK
(QHOHOGHORVGHSRVLWDQWHVPiV´FKLFRVµ WHQtDQHOGHOWRWDOGHGHSyVLWRV
PLHQWUDV TXH HO GH ORV GHSRVLWDQWHV PiV ´JUDQGHVµ DSRUWDEDQ WDPELpQ HO GHO
WRWDO GH SDVLYR EDQFDULR
$ HVD IHFKD KDEtD GHSRVLWDQWHV GHO VHFWRU QR
ILQDQFLHUR FRQ XQ GHSyVLWR SURPHGLR FDGD XQR HTXLYDOHQWH D 86 $GHPiV
DSUR[LPDGDPHQWHHOGHOQ~PHURWRWDO GH GHSRVLWDQWHV WHQtDQ GHSyVLWRV HTXLYDOHQWHV
DO GH ODV UHVHUYDV EDQFDULDV H[LVWHQWHV D HVD IHFKD XQRV 86 PLOORQHV GH
GyODUHV
(VWR LQGLFD TXH OD LQTXLHWXG VREUH HO ULHVJR HQ OD FRQFHQWUDFLyQ GH ORV GHSyVLWRV HV
DSOLFDEOH D OD UHDOLGDG GH QXHVWUR VLVWHPD ILQDQFLHUR $ SHVDU GH REVHUYDUVH XQ PD\RU
ULHVJR HQ HVWD HVWUXFWXUD GH ILQDQFLDPLHQWR GHEH H[LVWLU DOJXQD UD]yQ SRU OD FXDO ORV
EDQFRV LJXDOPHQWH OD DGRSWDQ (VWR SXHGH GHEHUVH D GRV PRWLYRV (O SULPHUR HV TXH
GHEHQ H[LVWLU PD\RUHV FRVWRV SRU OD FDSWDFLyQ \ DGPLQLVWUDFLyQ GH ORV GHSyVLWRV (O
15
6L WRGRV ORV GHSRVLWDQWHV UHWLUDUiQ VXV GHSyVLWRV GH DFXHUGR D XQD YDULDEOH %HUQRXOOL LQGHSHQGLHQWHV \ FRQ OD PLVPD
SUREDELOLGDGHQWRQFHVHOSHRUHVFHQDULRTXHVHUHWLUHWRGRHOSDVLYRHVFODUDPHQWHVXSHULRUFRQXQVRORGHSRVLWDQWH
,QWHQWpDQDOL]DUHVWRVGDWRVSDUDYHUODHYROXFLyQGHODFRQFHQWUDFLyQGHGHSyVLWRVSUH\SRVWFULVLVEDQFDULDGHO
\GHWHUPLQDUVLORVJUDQGHVGHSyVLWRV´UHWLUDURQSULPHURTXHHOUHVWRµSHURORVGDWRVQRHVWiQGLVSRQLEOHV
18
VHJXQGRPRWLYRHVWDUtDYLQFXODGRFRQODGHFLVLyQGHGHSyVLWRVGHORVLQGLYLGXRV$OJXQRV
RSWDUiQSRUGHSRVLWDUVXVIRQGRVHQXQDRSRFDVLQVWLWXFLRQHVILQDQFLHUDVWDOYH]SRUHO
PLVPR PRWLYR GH FRVWRV GH PDQHMR R SRU FXHVWLRQHV UHIHULGDV D OD VHJXULGDG TXH OH
PHUH]FDFDGDLQVWLWXFLyQ
3DUD DQDOL]DU HVWH WHPD QRV EDVDUHPRV HQ XQ PRGHOR SUHVHQWDGR HQ 5LQJERP 6K\
&
6WHQEDFNDTXHFDUDFWHUL]DXQDIXQFLyQGHEHQHILFLRVHVSHUDGRV\ODSUREDELOLGDG
HQHOULHVJRGHOLTXLGH]GHXQEDQFRFRPHUFLDO$GLIHUHQFLDGHHVHWUDEDMRTXHVXSRQH
RHQHOTXHORVDXWRUHVVXSRQHQTXHODYDULDEOHDOHDWRULDGHUHWLURVDJUHJDGRVWLHQHXQD
GLVWULEXFLyQQRUPDOQXHVWURDQiOLVLVQRVHOLPLWDDXQGHWHUPLQDGRWLSRGHGLVWULEXFLyQ
0RGHOR
6XSyQJDVHTXHKD\GRVEDQFRV$\%FRQGHSyVLWRVQRUPDOL]DGRVDXQR&DGDEDQFRWLHQH
GLVWLQWRVGHSRVLWDQWHV
$FWLYRV
(Q HO SHUtRGR W ORV EDQFRV UHFLEHQ ORV GHSyVLWRV GH ORV LQGLYLGXRV (O EDQFR WDPELpQ
HQ HVWH SHUtRGR GHFLGH TXH TXp SURSRUFLyQ GH HVRV IRQGRV LQYHUWLU HQ XQ DFWLYR
OtTXLGR
e VLQ UHQWDELOLGDG \ HO UHVWR UHVWR LQYHUWLUORV HQ XQ DFWLYR LOtTXLGR (VWH
~OWLPR DFWLYR VH UHDOL]D HQ W FRQ XQD UHQWDELOLGDG FLHUWD QHWD LJXDO D
r FRQ
0 ≤ r < 1
3DVLYRV
6HD
) i HOGHSyVLWRGHOLQGLYLGXR i HQW
HQHOEDQFR$\RUGHQDGRVGHWDOIRUPDTXH
0 t ) 1 t ) 2 t. . . t ) n t 1 FRQ ∑ α i = 1 6HD * i HOGHSyVLWRGHOLQGLYLGXR i HQW
n
1
HQ HO EDQFR % WDPELpQ RUGHQDGRV HQ IRUPD FUHFLHQWH
n
∑β
i
0 t *1 t *2 t. . . t *n t 1 FRQ
= 1 6XSRQJDPRVTXHHOEDQFR$WLHQHGHSyVLWRVPHQRVFRQFHQWUDGRVTXHHOEDQFR
1
% 6HJ~Q QXHVWUD GHILQLFLyQ GH FRQFHQWUDFLyQ HVWR LPSOLFD TXH
k
k
1
1
∑αi ≥ ∑ βi SDUD
&KLFRVVRQORVTXHWHQtDQGHSyVLWRVPHQRUHVD86\JUDQGHVORVTXHWHQtDQGHSyVLWRVPD\RUHVD86
$VXPLPRVTXHORVGHSRVLWDQWHVSXHGHQWHQHUGHSyVLWRVLJXDOHVDFHUR
19
k = 1, 2,..., n 6XSRQHPRV LJXDOPHQWH TXH H[LVWH XQ FRVWR SRU GLYHUVLILFDU ORV GHSyVLWRV
FRVWRV GH FDSWDFLyQ GH GHSyVLWRV FRVWRV DGPLQLVWUDWLYRV \ RWURV VLPLODUHV SDUD
VLPSOLILFDUHODQiOLVLV\TXHHVWRVFRVWRVVRQILMRV\VRQFUHFLHQWHVFRQODGLYHUVLILFDFLyQ
GHO SDVLYR 6HD
CF A \ CFB ORV FRVWRV ILMRV GHO EDQFR $ \ % UHVSHFWLYDPHQWH VLHQGR
CF A ! CFB 5HWLURV$JUHJDGRV
(Q W FDGD GHSRVLWDQWH UHFLEH XQ VKRFN UHDO GH OLTXLGH] GH DFXHUGR D XQD YDULDEOH
DOHDWRULD
X i GLVWULEXFLyQ FRQRFLGD SRU ORV EDQFRV $VXPDPRV TXH HVWD YDULDEOH VH
GHILQHGHIRUPDWDOTXHORVUHWLURVVHUiQLJXDOHVDXQDVXPDLJXDOD
α i X i HQHOEDQFR$
0 t ) i X i t ) i \DXQDVXPDLJXDOD β i X i HQHOEDQFR% 0 ≤ β i X i ≤ β i 'HODPLVPD
IRUPD TXH HQ HO HMHPSOR ORV UHWLURV DJUHJDGRV VRQ XQD IXQFLyQ GHO YHFWRU GH GHSyVLWRV
LQLFLDOHV\VHUiQLJXDOHVD
∑1n α i X i SDUDHOEDQFR$HLJXDOHVD ∑1 β i X i SDUDHOEDQFR%
n
6XSRQJDPRVTXHOD GLVWULEXFLyQ DFXPXODGD GH HVWRV UHWLURV DJUHJDGRV VRQ
F (x) \ G (x)
UHVSHFWLYDPHQWH
,QVXILFLHQFLDVGH5HVHUYDV
6L HQ W HO DFWLYR OtTXLGR QR DOFDQ]D SDUD FXEULU OD GHPDQGD SRU UHVHUYDV HO %DQFR
&HQWUDO TXH VLJXH XQD SROtWLFD GH UHVFDWH GH EDQFRV FRQ SUREOHPDV GH OLTXLGH] DFW~D
FRPR SUHVWDPLVWD GH ~OWLPD LQVWDQFLD (VWH SUpVWDPR VH UHDOL]D D XQD WDVD GH
SHQDOL]DFLyQPD\RUDOUHQGLPLHQWRGHODFWLYRLOtTXLGR$VXPDPRVWDPELpQTXH HVWD WDVD
r
GHSHQDOL]DFLyQHV m !
r (QW
HOEDQFRUHDOL]D VXV DFWLYRV \ OR GLVWULEX\H HQWUH WRGRV
VXVSDVLYRV
%DQFR&HQWUDO
(Q W HO %DQFR &HQWUDO DFW~D FRPR SUHVWDPLVWD GH ~OWLPD LQVWDQFLD \ UHVFDWD D ORV
EDQFRV FRQ GLILFXOWDGHV GH OLTXLGH] 6L ORV UHWLURV VXSHUDQ D ODV UHVHUYDV EDQFDULDV
3DUDVLPSOLILFDUODQRWDFLyQVXSRQJDPRVTXHHVWDYDULDEOHHVFRQWLQXD
20
H[LVWHQWHVHOUHVFDWHVHUiLJXDODODGLIHUHQFLD(QFDPELRVLORVUHWLURV
x QRVXSHUDQD
ODV UHVHUYDV GH ORV EDQFRV FRPHUFLDOHV HO UHVFDWH VHUi LJXDO D FHUR 'HILQDPRV SRU OR
WDQWRODYDULDEOHDOHDWRULD
S (x) TXHVRQORVUHFXUVRVTXHSUHVWDHO%DQFR&HQWUDOSDUD
ILQDQFLDUHOIDOWDQWHFDXVDGRSRUHOH[FHVRGHGHPDQGDSRUUHVHUYDV\TXHVHUiLJXDOD
S ( x) = x − e VL x > e
S ( x) = 0 VL x ≤ e
%DQFRV&RPHUFLDOHV
(Q IXQFLyQ GH ORV GDWRV DQWHULRUHV OD IXQFLyQ GH EHQHILFLRV HVSHUDGD SDUD FDGD EDQFR
VHUiUHVSHFWLYDPHQWH
1
E F (π (e F )) = (1 − e F )r − rm ∫ ( x − e F )dF ( x) − CF A
eF
\
1
E G (π (e G )) = (1 − eG )r − rm ∫ ( x − e G )dG ( x) − CFB
eG
'RQGH HO SULPHU WpUPLQR GH FDGD LJXDOGDG UHSUHVHQWD OD UHQWDELOLGDG HVSHUDGD GH OD
LQYHUVLyQ HQ HO DFWLYR LOtTXLGR HO VHJXQGR WpUPLQR HV OD PXOWD HVSHUDGD TXH GHEHUi
SDJDUVH SRU WHQHU LQVXILFLHQFLD GH UHVHUYDV \ HO WHUFHU WpUPLQR VRQ ORV FRVWRV ILMRV SRU
GLYHUVLILFDU HO SDVLYR &RQ HVWH VHQFLOOR PRGHOR SRGHPRV H[WUDHU DOJXQDV LQWHUHVDQWHV
FRQFOXVLRQHVTXHVXUJHQSRUODFRQFHQWUDFLyQGHORVGHSyVLWRVLQLFLDOHV(QSULPHUOXJDU
YHDPRVHOULHVJRHQODGLVWULEXFLyQGHORVUHWLURV
¢&XiOGHORVGRVEDQFRVWLHQHODGLVWULEXFLyQGHUHWLURVGHPD\RUULHVJR"
3URSRVLFLyQ
(O EDQFR FRQ GHSyVLWRV PiV FRQFHQWUDGRV WHQGUi OD GLVWULEXFLyQ GH UHWLURV GH PD\RU
ULHVJR(VGHFLUODGLVWULEXFLyQGHUHWLURVGHOEDQFR%VHUiPiVULHVJRVDTXHODGHOEDQFR
$
$VXPDPRVTXHOD F
\
G VRQHVWULFWDPHQWHFUHFLHQWHV
21
'HPRVWUDFLyQ
$O VHU ORV UHWLURV DJUHJDGRV GH ORV EDQFRV $ \ % LJXDOHV D
UHVSHFWLYDPHQWH \ DO KDEHU VXSXHVWR TXH
k
k
1
1
∑1n α i X i \
∑1n β i X i
∑ α i ≥ ∑ β i SDUD k = 1, 2,..., n (QWRQFHV VH
FXPSOHQODVKLSyWHVLVGHOWHRUHPD\SRGHPRVGHFLUTXH
∑1n α i X i
2
∑1n β i X i
4('
¢&yPR LQIOX\H OD FRQFHQWUDFLyQ GH ORV GHSyVLWRV EDQFDULRV HQ ORV IRQGRV GH
UHVFDWHGHO%DQFR&HQWUDO"
/DPHQWDEOHPHQWHDSHVDUGHVDEHUTXHODGLVWULEXFLyQGHORVUHWLURVGHOEDQFR%HVPiV
ULHVJRVD TXH OD GHO EDQFR $ QR SRGHPRV GHWHUPLQDU D SULRUL FXiO GH ORV GRV EDQFRV
PDQWHQGUi PD\RUHV UHVHUYDV SXHV ODV UHVHUYDV ySWLPDV TXH UHVXHOYHQ OD PD[LPL]DFLyQ
GHODVIXQFLRQHVGHEHQHILFLRVFRPHUFLDOHVVXUJHQGH
F (e F* ) = G (eG* ) = 1 −
r
rm
(Q ORV WUDEDMRV GH /LFDQGUR H ,OODQHV VH DQDOL]D ODV UHVHUYDV OtTXLGDV TXH
GHEHUtD WHQHU HO %DQFR &HQWUDO SDUD FXEULU GHWHUPLQDGRV WLSRV GH ULHVJRV ILQDQFLHURV
HQWUHHOORVHOUHIHULGRDXQDFRUULGDEDQFDULD$SHVDUGHVDEHUTXHODGLVWULEXFLyQGHORV
UHWLURVGHOEDQFR%HVPiVULHVJRVDTXHODGHOEDQFR$QRSRGHPRVGHWHUPLQDUDSULRUL
FXiO GH ORV GRV EDQFRV PDQWHQGUi PD\RUHV UHVHUYDV OtTXLGDV 6LQ HPEDUJR FRPR
FRQVHFXHQFLDGHODSURSRVLFLyQSRGHPRVYHUDOJXQRVUHVXOWDGRVLQWHUHVDQWHV
3URSRVLFLyQ
6LHOEDQFR%WXYLHUDXQQLYHOGHUHVHUYDVPHQRUHVRLJXDOHVDODVGHOEDQFR$HQWRQFHV
HO%DQFR&HQWUDOHVSHUDUiGHVWLQDUOHPD\RUHVSUpVWDPRVSRUUHVFDWHDOEDQFR%
'HPRVWUDFLyQ
3RUODSURSRVLFLyQDQWHULRUVDEHPRVTXHODGLVWULEXFLyQGHORVUHWLURVGHOEDQFR%HVPiV
ULHVJRVD TXH OD GHO EDQFR $ 6XSRQJDPRV TXH ODV UHVHUYDV ySWLPDV GH FDGD EDQFR HV OD
6LHOEDQFR%WXYLHUDXQPHQRUQLYHOGHUHVHUYDVTXHODVGHOEDQFR$ODDVLVWHQFLDHVSHUDGDVHUtDD~QPD\RU
22
PLVPDHLJXDODXQYDORU
c FRQ 0 ≤ c ≤ 1 (QWRQFHVODDVLVWHQFLDHVSHUDGDSDUDHOEDQFR
$VHUiLJXDOD
c
1
1
0
c
c
E F ( S ( x)) = ∫ 0dF ( x) + ∫ ( x − c)dF ( x) = ∫ ( x − c)dF ( x)
2SHUDQGRHLQWHJUDQGRSRUSDUWHVHVWDH[SUHVLyQREWHQHPRV
1
E F ( S ( x)) = 1 − c − ∫ F ( x)dx
c
\GHODPLVPDPDQHUDODDVLVWHQFLDHVSHUDGDSDUDHOEDQFR%HV
1
E G ( S ( x)) = 1 − c − ∫ G ( x)dx c
3RU ODV SURSLHGDGHV GH GRPLQDQFLD HVWRFiVWLFD YLVWDV HQ OD SULPHUD VHFFLyQ DO VHU
F
2
G VH
FXPSOH
TXH
1
1
c
c
∫ F ( x)dx ≥ ∫ G ( x)dx ∀c ∈ [0,1] \
SRU
OR
WDQWR
E F ( S ( x)) ≤ E G ( S ( x)) 6L ODV UHVHUYDV GHO EDQFR % IXHUDQ PHQRUHV D ODV GHO EDQFR $ HVWD ~OWLPD GHVLJXDOGDG
REYLDPHQWHVHFXPSOLUtD
4('
(OLPSDFWRVREUHODDVLVWHQFLDEUXWDVHUiGLVWLQWRDSHVDUGHWUDWDUVHGHGRVEDQFRVFRQ
LJXDOSDVLYR(OHIHFWRQHJDWLYRGHHVWRHVHYLGHQWHHQXQDHFRQRPtDGRODUL]DGDFRPROD
GH QXHVWUR SDtV HQ OD TXH XQ JUDQ SRUFHQWDMH GH ORV GHSyVLWRV HVWiQ QRPLQDGRV HQ HVD
PRQHGD (O %DQFR &HQWUDO QR FXHQWD FRQ UHVHUYDV LOLPLWDGDV GH HVD PRQHGD H[WUDQMHUD
SDUDDVLVWLUDEDQFRVFRQSUREOHPDVGHOLTXLGH]
&RPR YLPRV HQ OD SURSRVLFLyQ VL ODV UHVHUYDV GHO EDQFR % IXHUDQ PHQRUHV D LJXDOHV D
ODV UHVHUYDV GHO %DQFR $ HQWRQFHV
E F ( S ( x)) ≤ E G ( S ( x)) \ ODV UHVHUYDV ySWLPDV GHO
%DQFR&HQWUDOGHEHUtDQFUHFHUFXDQWRPiVULHVJRVDVHDODGLVWULEXFLyQGHORVUHWLURV
'HDKtHOSHOLJURGHQRWHQHUHQFXHQWDODFRQFHQWUDFLyQGHORVGHSyVLWRVSDUDODILMDFLyQ
GHORVHQFDMHV REOLJDWRULRV EDQFDULRV 6L HVWDUHVWULFFLyQ IXHUD WDO TXH ORV GRV EDQFRV VH
YLHUDQREOLJDGRVDHVFRJHUHOPLVPRQLYHOGHHQFDMHHQWRQFHVHO%DQFR&HQWUDOGHEHUtD
23
HVSHUDU XQD PD\RU DVLVWHQFLD GH IRQGRV FXDQWR PD\RU IXHUD OD FRQFHQWUDFLyQ GH ORV
GHSyVLWRV
&21&/86,21(6
(OSUHVHQWHWUDEDMRGHPRVWUyXQQXHYRWHRUHPDTXHQRVSHUPLWHRUGHQDUODGRPLQDQFLD
HVWRFiVWLFD GH VHJXQGR RUGHQ HQWUH FRPELQDFLRQHV OLQHDOHV FRQYH[DV GH YDULDEOHV
DOHDWRULDV VLHQGR HVWH XQ DSRUWH DGLFLRQDO D ORV UHVXOWDGRV HQFRQWUDGRV SRU +DGDU \
5XVVHOO7HVIDWVLRQ\/L\:RQJ(VWHWHRUHPDSHUPLWLyPRVWUDUTXH
EDMR GHWHUPLQDGDV KLSyWHVLV OD GLVWULEXFLyQ GH ORV UHWLURV EDQFDULRV HV PiV ULHVJRVD
FXDQWRPiVFRQFHQWUDGRVHVWpQORVGHSyVLWRV'RVFRQFOXVLRQHVVXUJHQGHHVWHSXQWR
(Q SULPHU OXJDU OD DVLVWHQFLD HVSHUDGD GH XQ %DQFR &HQWUDO VH LQFUHPHQWD FXDQWR PiV
FRQFHQWUDGRV HVWiQ ORV GHSyVLWRV EDQFDULRV 6L HO %DQFR &HQWUDO DFWXDUD FRPR
SUHVWDPLVWD GH ~OWLPD LQVWDQFLD GHEHUtD HVSHUDU XQD PD\RU DVLVWHQFLD GH IRQGRV D ORV
EDQFRVFRQXQDHVWUXFWXUDGHGHSyVLWRVPiVFRQFHQWUDGD
(Q VHJXQGR OXJDU VL HO %DQFR &HQWUDO WXYLHUD FRPR SROtWLFD GH UHJXODFLyQ ILMDU ORV
HQFDMHV REOLJDWRULRV GH ORV EDQFRV FRPHUFLDOHV GHEHUtD H[LJLUOH XQ PD\RU QLYHO GH
HQFDMHDORVEDQFRVFRQGHSyVLWRVPiVFRQFHQWUDGRV(QFRQVHFXHQFLDODSROtWLFDDFWXDO
VHJXLGD SRU HO %DQFR &HQWUDO GHO 8UXJXD\ VREUH HQFDMHV PtQLPRV REOLJDWRULRV QR VHUtD
FRUUHFWD
(QFRQFOXVLyQODFRQMHWXUDVREUHODFRQFHQWUDFLyQHQORVGHSyVLWRVGHEHUtDVHUWHQLGDHQ
FXHQWD HQ HVSHFLDO HQ PRPHQWRV GH FULVLV ILQDQFLHUD (Q WLHPSRV HQ ORV TXH H[LVWD XQ
FUHFLPLHQWR FRQWLQXR HQ ORV GHSyVLWRV VHUtD GH HVSHUDU TXH QR H[LVWDQ ORV ULHVJRV
DVRFLDGRV D OD FRQFHQWUDFLyQ SXHV XQ JUDQ GHSyVLWR TXH VH UHWLUD HV FRPSHQVDGR FRQ
QXHYRVGHSyVLWRVTXHLQJUHVDQDOEDQFR3HURHQPRPHQWRVGHFULVLVILQDQFLHUDFXDQGRHO
WRWDOGHORVGHSyVLWRVGHFUHFHODFRQMHWXUDSDUHFHPiVDSOLFDEOH\HOULHVJRSDUHFHVHU
PD\RU $TXHOORV EDQFRV FRQ GHSyVLWRV PX\ FRQFHQWUDGRV HVWDUtDQ VXMHWRV D OD YROXQWDG
GHXQRVSRFRVLQGLYLGXRVHQODGLQiPLFDGHVXILQDQFLDPLHQWR
24
5()(5(1&,$6
%ROWRQ 3 \ 6KDUIVWHLQ ' 2SWLPDO GHEW VWUXFWXUH DQG WKH QXPEHU RI FUHGLWRUV
-RXUQDORI3ROLWLFDO(FRQRP\
%U\DQW$PRGHORIUHVHUYHVEDQNUXQVDQGGHSRVLWLQVXUDQFH-RXUQDORI%DQNLQJ
DQG)LQDQFH
&RUVHWWL'DVJXSWD0RUULV \ 6KLQ 'RHV RQH 6RURV PDNH D GLIIHUHQFH" $ WKHRU\ RI
FXUUHQF\FULVLVZLWKODUJHDQGVPDOOWUDGHUV5HYLHZRI(FRQRPLF6WXGLHVYRO
'LDPRQG \ '\EYLJ %DQN UXQV GHSRVLWV LQVXUDQFH DQG OLTXLGLW\ -RXUQDO RI
3ROLWFDO(FRQRP\
)UHL[DV\5RFKHW0LFURHFRQRPLFVRIEDQNLQJ0,73UHVV
*ROOLHU7KH(FRQRPLFVRI5LVNDQG7LPH0,73UHVV
+DGDU \ 5XVVHOO 6WRFKDVWLF GRPLQDQFH DQG GLYHUVLILFDWLRQ -RXUQDO RI (FRQRPLF
7KHRU\
+DQRFK\/HY\7KHHIILFLHQF\DQDO\VLVRIFKRLFHLQYROYLQJULVN5HYLHZRI(FRQRPLF
6WXGLHV
/L \ :RQJ ([WHQVLRQ RI VWRFKDVWLF GRPLQDQFH WKHRU\ WR UDQGRP YDULDEOHV 5$,52
5HFKHUFKH2SpUDWLRQQHOOH
/LFDQGUR-$8QDHYDOXDFLyQGHODVUHVHUYDVLQWHUQDFLRQDOHVGHO%&85HYLVWDGH
(FRQRPtD%&8
,OODQHV-1LYHOySWLPRGHUHVHUYDVLQWHUQDFLRQDOHVHQ8UXJXD\%&8'RFXPHQWR
0F&DQGOHVV(QVXULQJILQDQFLDOVWDELOLW\ZLWKODUJHGHSRVLWRUV:RUNLQJ3DSHU
%DQFR&HQWUDO5HS~EOLFD$UJHQWLQD
0LWULQRYLN'(OHPHQWDU\LQHTXDOLWLHV*URQLJHQ31RRUGKRII
2N(IH3UREDELOLW\7KHRU\ZLWK(FRQRPLF$SSOLFDWLRQERRNGUDIW
2OLYHUD -XOLR +* 7KH 6TXDUH 5RRW /DZ RI 3UHFDXWLRQDU\ UHVHUYHV -RXUQDO RI
3ROLWLFDO(FRQRP\
5LQJERP 6K\
& 6WHQEDFND 2SWLPDO /LTXLGLW\ 0DQDJHPHQW DQG %DLO2XW 3ROLF\ LQ
WKH%DQNLQJ,QGXVWU\-RXUQDORI%DQNLQJDQG)LQDQFH
5RFKHW\9LYHV&RRUGLQDWLRQIDLOXUHVDQGWKHOHQGHURIODVWUHVRUW:3,16($'
5RWVFKLOG\6WLJOLW],QFUHDVLQJULVN,DGHILQLWLRQ-RXUQDORI(FRQRPLF7KHRU\
5RWVFKLOG \ 6WLJOLW] ,QFUHDVLQJ ULVN ,, LWV HFRQRPLF FRQVHTXHQFHV -RXUQDO RI
(FRQRPLF7KHRU\
25
5RWVFKLOG\6WLJOLW]6RPHIXUWKHUQRWHVRQWKHPHDVXUHPHQWRILQHTXDOLW\-RXUQDO
RI(FRQRPLF7KHRU\
6DPXHOVRQ 3DXO *HQHUDO SURRI WKDW GLYHUVLILFDWLRQ SD\V -RXUQDO RI )LQDQFH DQG
4XDQWLWDWLYH$QDO\VLV
7HD'HORLWWH7RXFK8UXJXD\,QIRUPHGHVLVWHPDILQDQFLHURGHO8UXJXD\
7HVIDWVLRQ6WRFKDVWLFGRPLQDQFHDQGPD[LPL]DWLRQRIH[SHFWHGXWLOLW\5HYLHZRI
(FRQRPLF6WXGLHV
7LUROH-7KH7KHR\RI&RUSRUDWH)LQDQFH3ULQFHWRQ3UHVV
26