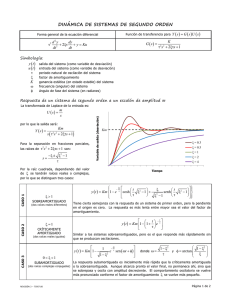
PS-1316 Tema 3.2 – Sistemas de Segundo Orden 2

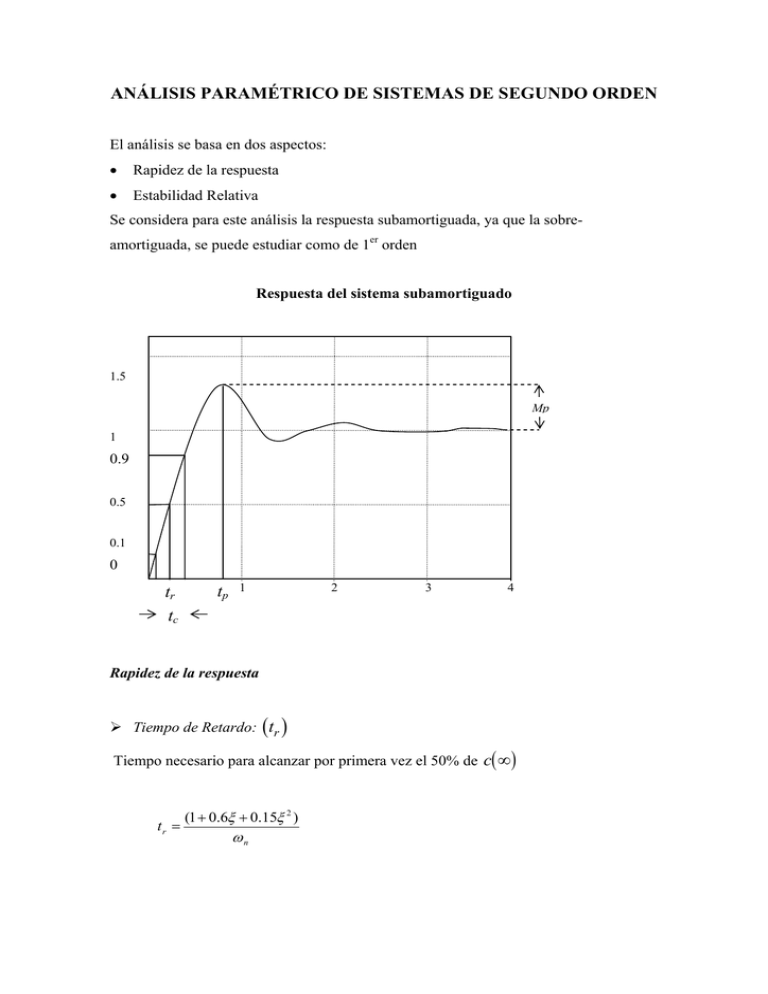
ANÁLISIS PARAMÉTRICO DE SISTEMAS DE SEGUNDO ORDEN
El análisis se basa en dos aspectos:
•
Rapidez de la respuesta
•
Estabilidad Relativa
Se considera para este análisis la respuesta subamortiguada, ya que la sobreamortiguada, se puede estudiar como de 1er orden
Respuesta del sistema subamortiguado
1.5
Mp
1
0.9
0.5
0.1
0
tr
tc
tp
1
2
3
4
Rapidez de la respuesta
¾ Tiempo de Retardo: (tr )
Tiempo necesario para alcanzar por primera vez el 50% de c( ∞)
tr =
(1 + 0.6ξ + 0.15ξ 2 )
ωn
¾ Tiempo de Crecimiento: (tc )
Tiempo necesario para ir desde el 10% hasta el 90 % de c( ∞)
t c = t90% − t10%
1 + 1.1ξ + 1.4ξ 2
=
ωn
( )
¾ Tiempo de Pico: t p
Es el tiempo que tarda la respuesta en alcanzar su primer máximo
tp =
π
ωn 1 − ξ 2
=
π
ωd
¾ Tiempo de Establecimiento: ( t s )
•
Criterio de 5%: Tiempo que tarda la respuesta en mantenerse dentro de 5% de
c( ∞) .
ts =
•
3
ξω
Criterio de 2%: Tiempo que tarda la respuesta en mantenerse dentro de 2% de
c( ∞) .
ts =
4
ξω
Estabilidad Relativa
( )
(
)
¾ Máximo pico M p y Máximo pico porcentual M p % .
Se define como máximo pico, a la diferencia de valores de la salida c(t) entre su primer
valor máximo, y su valor en estado estacionario c( ∞) , (es decir, es el valor relativo del
primer máximo respecto al valor final).
( )
c(t p ) − c( ∞)
⎛
× 100 = e − πξ /
%=
M p = c t p − c( ∞)
Mp
c( ∞)
1− ξ 2
⎜
⎝
⎞
⎟ × 100
⎠
DISCUSIÓN:
•
La velocidad de caída del transitorio depende de τ =
1
ξω n
. Para un valor dado de
ω n , si ξ aumenta (ξ → 1) , t s disminuye. (En los sistemas sobreamortiguados, t s
puede ser mayor ya que se tarda la inicialización de la respuesta).
•
El valor de Mp depende solo de ξ .
Evolución del máximo pico (Mp) con ξ
En general, ξ esta fijada por un requerimiento de Mp , por lo tanto, para mejorar
t s habrá que aumentar ω n .
CONCLUSIONES
Las características de la respuesta transitoria para los sistemas de 2do orden
subamortiguado depende de los parámetros ξ y ω n ; es decir de la ubicación de los
polos de lazo cerrado: s1,2 = − ξω n ± jω d
ω n 2 = ω d 2 + (ξω n )2 = ω n 2 (1 − ξ 2 ) + ω n 2ξ 2
ξω n
cos(θ ) =
= ξ ⇒ θ = arcos(ξ )
ωn
Ubicación de las raíces para: (a) ωn constante, (b) ξ constante, (c) α constante,
(d) ω constante
Jw
Amortiguamiento jw
positivo
ws1>ws2>ws3
Amortiguamiento
ζ4
negativo
Plano s
ζ3
ζ=0
ws2
plano s
ws1
s
0
ws3
ζ2
ζ=0
ζ1
Amortiguamiento
(a)
Amortiguamiento
Positivo
Amortiguamiento
Positivo
Jw
Amortiguamiento
Negativo
s
0
(b)
negativo
jw
plano s
w2
w1
-σ3
-σ2
0
σ1
Amortiguamiento
Positivo
s
Amortiguamiento
(c)
Negativo
0
-w1
-w2
(d)