Proceso estacional de la demanda

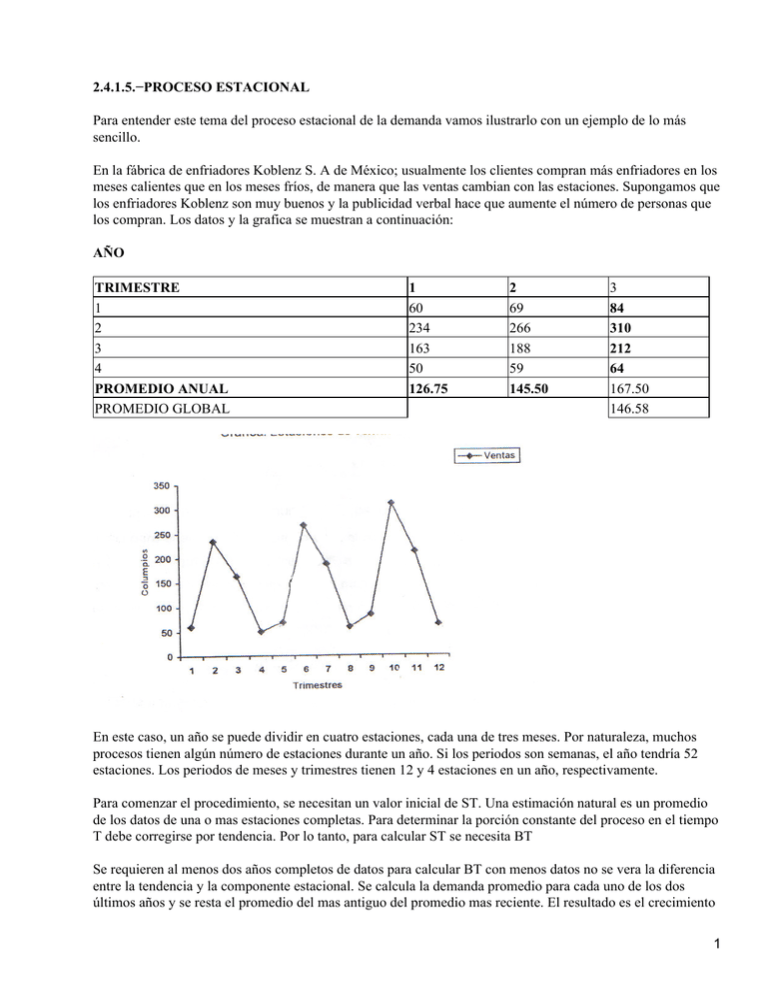
2.4.1.5.−PROCESO ESTACIONAL
Para entender este tema del proceso estacional de la demanda vamos ilustrarlo con un ejemplo de lo más
sencillo.
En la fábrica de enfriadores Koblenz S. A de México; usualmente los clientes compran más enfriadores en los
meses calientes que en los meses fríos, de manera que las ventas cambian con las estaciones. Supongamos que
los enfriadores Koblenz son muy buenos y la publicidad verbal hace que aumente el número de personas que
los compran. Los datos y la grafica se muestran a continuación:
AÑO
TRIMESTRE
1
2
3
4
PROMEDIO ANUAL
PROMEDIO GLOBAL
1
60
234
163
50
126.75
2
69
266
188
59
145.50
3
84
310
212
64
167.50
146.58
En este caso, un año se puede dividir en cuatro estaciones, cada una de tres meses. Por naturaleza, muchos
procesos tienen algún número de estaciones durante un año. Si los periodos son semanas, el año tendría 52
estaciones. Los periodos de meses y trimestres tienen 12 y 4 estaciones en un año, respectivamente.
Para comenzar el procedimiento, se necesitan un valor inicial de ST. Una estimación natural es un promedio
de los datos de una o mas estaciones completas. Para determinar la porción constante del proceso en el tiempo
T debe corregirse por tendencia. Por lo tanto, para calcular ST se necesita BT
Se requieren al menos dos años completos de datos para calcular BT con menos datos no se vera la diferencia
entre la tendencia y la componente estacional. Se calcula la demanda promedio para cada uno de los dos
últimos años y se resta el promedio del mas antiguo del promedio mas reciente. El resultado es el crecimiento
1
en los dos años, que debe convertirse en un crecimiento estacional dividiendo entre L, el número de estaciones
por año. Si se cuentan con más de dos años de datos, pueden usarse cualquiera de ellos para estimar la
pendiente. Si se usan el primero y el ultimo, con m años de datos disponibles, se divide entre (m − 1)L en
lugar de L para obtener el crecimiento por periodo.
Entonces BT y ST iniciales para enfriadores Koblenz; determinaremos los parámetros para el método
estacional de Winster usando los datos de la tabla anterior.
Solución:
El promedio del tercer año (ultimo cuatro datos) es
El promedio para el segundo para el segundo año es de d2 = 145.5 restando el promedio para el año 2 del
promedio para el año 3 sé obtiene el crecimiento de un año. Estos promedios se centran en el punto medio de
cada año, los periodos 6.5 y 10.5, respectivamente; de manera que hay un año entre ellos. Se divide entre 4
para obtener el crecimiento por periodo. Se tiene:
Dada una estimación de la tendencia, se puede calcular una estimación de la componente constante. El
promedio de todos los datos se centra en (T − 2)/2, el punto medio de las observaciones, o (T − 1)/2 periodos
de T, el tiempo presente. Se puede estimar la porción constante del modelo en el tiempo T multiplicando la
tendencia por periodos, BT , por
(T − 1) /2, el número de periodos que hay entre el centro y T. Entonces el promedio global para el ejemplo es:
Como hay doce periodos de datos, D esta centrado en el periodo 6.5, de manera que la estimación inicial del
término constante, ST en el periodo 12 seria entonces:
Una vez que se tienen BT y ST una estimación natural del factor estacional parecería ser la demanda en el
periodo dividida entre el término constante. Pero ojo debe corregirse por la parte de tendencia de la constante.
La estimación para la porción constante ST de manera que reflejara el proceso en el tiempo T. Intuitivamente,
la porción constante del proceso en (t − 1) debe ser mas pequeño en BT y mas pequeño en 2BT y (t − 2). En
general, una estimación de la porción constante del proceso para el periodo t(t < T) es la estimación de la
constante en el tiempo T menos la estimación de la tendencia multiplicada por el número de periodos, esto es,
BT − ST (T − 1). Una vez hecho el ajuste por tendencia, se puede dividir la demanda real entre este valor
ajustado, para obtener una estimación del factor estacional. Se calculan los factores estacionales usando la
formula siguiente:
Donde Ct es la estimación de Ct se promedian los factores estacionales para la misma estación de cada año
para eliminar el ruido.
Estos factores estacionales, sin embargo, no necesariamente suman L. para normalizarlos primero se
determina R, el cociente de la duración de la estimación entre la suma de los factores estacionales:
Esta razón se multiplica por los factores estacionales que se tienen para obtener nuevos es:
Ejemplo de Factores estacionales iniciales. Calcular los factores estacionales iniciales para los datos de la
tabla 8.
Solución.
Para calcular una estimación del factor estacional para el periodo 1 en el ejemplo, se divide dt entre el término
2
constante para el periodo 1. el termino constante ajustado será:
Se divide d1 = 60 entre 116.33 y da C1 = 0.51, las ventas del primer trimestre de los años 2 y 3 se hace C9
igual al promedio de los tres. La tabla siguiente muestra cálculos similares, para el resto de los datos. La
última columna normaliza los factores estacionales.
AÑO
1
2
3
4
0.51 0.59 0.72 0.60 0.51
1.92 2.18 2.54 2.21 1.88
1.27 1.47 1.66 1.46 1.24
0.37 0.44 0.48 0.43
3