02-2 MODELIZACIÓN UNIVARIANTE ESTACIONAL
Anuncio

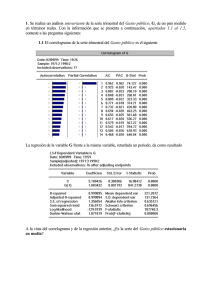
MODELIZACIÓN UNIVARIANTE ESTACIONAL Prof. Adriá Adrián Ferná Fernández CURSO METODOS CUANTITATIVOS AVANZADOS Opció Opción Econometrí Econometría Edició Edición 2009 Contenido 1. Introducción 2. Modelos SARIM 3. AMB 4. Filtros Lineales 1 Contenido 1. Introducción • Componentes • Estimació Estimación de Componentes • Modelizació Modelización paramé paramétrica • Modelizació Modelización no paramé paramétrica Componentes Una serie de tiempo puede ser caracterizada por los siguientes componentes: • • • • Tendencia de largo plazo. Variación cíclica. Variación estacional. Variación residual. Series de tiempo de frecuencia menor al añ año (mensuales, trimestrales) pueden presentar estacionalidad. estacionalidad. Es decir, son series con ciclos u oscilaciones perió periódicas, donde el perí período es igual o inferior al añ año. La presencia de este componente se explica por la existencia de las estaciones y los cambios climá climáticos (que impactan sobre la actividad), las costumbres (el fin de añ año, que es estrictamente cultural), etc. 2 Estimación de componentes El interés por el análisis de los componentes de series de tiempo tiene un fuerte aumento luego de la crisis de 1929, donde surge la preocupación por analizar (fechar) los ciclos económicos, detectar tempranamente sus puntos de giro (los picos y los valles, que dan lugar a recesiones y expansiones) y en general pronosticar sus movimientos. En aquellos tempranos años los componentes fueron generalmente especificados a partir de modelos determinísticos que podían ser estimados por regresión simple. Estimación de componentes En el enfoque paramétrico se parte de la especificación explícita de un modelo estadístico para la serie de tiempo observada o bien para los componentes. En algunas aplicaciones se supone la existencia de un modelo determinístico; mientras que en otras se supone que los modelos son estocásticos. Modelos determiní determinísticos A cada componente se le asigna una funció función determiní determinística Modelos estocá estocásticos Modelizació Modelización ARIMA con aná análisis de intervenció intervención (ARIMA(ARIMA-IA) 3 Estimación de componentes Tomamos la definición de Kaiser y Maravall: los modelos determinísticos son aquellos que arrojan un pronóstico con error cero cuando los parámetros del modelos son conocidos. Los modelos estocásticos proveerán pronósticos con errores aleatorios no nulos aún cuando los parámetros fuesen conocidos. Una vez que los modelos han sido identificados la estimación de los componentes se realiza utilizando estimadores óptimos dadas las restricciones impuestas por el modelo. Modelización paramétrica SEATS es la aplicación más reciente del enfoque paramétrico, también conocido como “basado en modelos”. Maravall lo define como Model-Based Approach. En otros artículos se refiere al método ARIMA-model-based (AMB). El programa TRAMO realiza los ajustes previos para poder llevar a cabo el ajuste estacional, el cual está basado en el trabajo de Gómez y Maravall (1994). El programa SEATS realiza el proceso de ajuste estacional. Originalmente desarrollados en el Banco de España fueron adoptados por Eurostat. 4 Modelización no paramétrica El enfoque no paramétrico (enfoque empírico) permite estimar los componentes no observados de una serie de tiempo sin recurrir a la especificación de un modelo estadístico para la serie de tiempo analizada . Usualmente bajo este enfoque, los componentes se estiman mediante la aplicación sucesiva de filtros lineales. La metodología de ajuste estacional utilizada en el programa X-12-ARIMA es el ejemplo más utilizado de este tipo de enfoque. X-12-ARIMA fue desarrollado por la oficina del censo de los Estados Unidos (U.S. Census Bureau) a partir de los programas de ajuste estacional Census X-11 (Shishkin et. al., 1967) y X-11-ARIMA (Dagum). Contenido 2. Modelos SARIMA • Modelos estacionales puros • Modelos estacionales multiplicativos • Correlograma • Modelos estacionales no estacionarios • Notació Notación 5 Modelos estacionales puros (1) ► Supóngase un fenómeno donde solamente existe relación entre observaciones de un mismo mes (trimestre, etc.) en dos años consecutivos. Por ej., para datos trimestrales: yt = C + φ y t − 4 + at con φ < 1 ► El valor corriente de yt se explica por el ruido contemporáneo y por el valor de y cuatro trimestres atrás (el mismo trimestre del año anterior). El modelo recoge factores estacionales exclusivamente. Modelos estacionales puros (2) ► El modelo puede ser escrito como: y t − φ y t − 4 = C + at (1 − φL4 ) yt = C + at Φ ( L ) yt = C + at donde Φ(L) es el polinomio autoregresivo. 6 Modelos estacionales puros (3) Designamos como “s” el período estacional (s=4 para datos trimestrales, s=12 para mensuales, etc.). El modelo anterior se nota como SAR(1)s, o modelo autoregresivo estacional (Seasonal en inglés) de primer orden. Es suficiente que φ en valor absoluto sea menor que 1 para que el modelo sea estacionario. Modelos estacionales puros (4) A continuación presentamos el correlograma de un modelo AR(1) y de un modelo SAR(1)4. 0,80 1 0,64 2 0,51 3 0,41 4 0,33 5 0,26 6 0,21 7 0,17 8 0,13 9 0,11 10 0,09 11 0,07 12 13 14 0,05 0,04 1 2 3 0,80 4 5 6 7 0,64 8 9 10 11 0,51 12 13 14 15 15 0,04 16 16 0,41 0,03 7 Modelos estacionales puros (5) La Función de Auto Correlación (FAC) del proceso estacional puro SAR(1)4 considerado anteriormente es: φ ρ =φk/s ρk = k − s 0 para k = s, 2s, 3s, ... en otro caso Otro modelo estacional puro - SAR(2)s: yt = C + φ1 y t − s + φ 2 y t − 2 s + at Modelos estacionales multiplicativos (1) Supóngase que se está modelizando el consumo de refrescos con datos de frecuencia trimestral. En el proceso de identificación del modelo se observa que los choques en el trimestre “t” repercuten también en el período o trimestre siguiente, y en el mismo trimestre del año siguiente. Es decir, provoca cambios en el componente estacional de la serie. 8 Modelos estacionales multiplicativos (2) Un modelo de medias móviles podría reflejar este comportamiento: yt = C + at −θ 1at −1 − θ 4 at − 4 Es decir, el ruido en “t” influye en “t+1” y en “t+4”. El modelo planteado tiene la limitación que no recoge la influencia que tendrá el efecto en “t+4” sobre el valor de la variable en “t+5”. Es decir, el efecto “un trimestre después” se modeliza solamente en “t+1”. Modelos estacionales multiplicativos (3) Una manera de salvar este problema es con la formulación de modelos estacionarios multiplicativos estacionales: yt = C + (1 −θ 1L )(1 − θ 4 L4 )at Reescribiendo el modelo: yt = C + at −θ 1at −1 − θ 4 at − 4 + θ1θ 4 at − 5 Es decir, el modelo justamente “captura” la interacción de los 2 efectos sobre el período “t+5”. 9 Modelos estacionales multiplicativos (4) Una forma alternativa de escribir el modelo anterior es como un MA(5): Yt = C + at −θ 1at −1 − θ 4 at − 4 − θ 5at −5 Esta última es la versión “no restringida”. Contiene un parámetro más que el modelo previo ya que justamente no impone la interacción entre los dos efectos. Si los modelos tuvieran un poder explicativo similar, siempre es preferible el primero (más parsimonioso). Modelos estacionales multiplicativos (5) La práctica ha llevado a adoptar los modelos multiplicativos como la representación general de efectos ordinarios y estacionales en procesos estacionarios. ► En todo caso, siempre es posible estimar ambos modelos y realizar pruebas de hipótesis para decidir por uno u otro. ► 10 Modelos estacionales multiplicativos (6) Otros ejemplos multiplicativos: de modelos (1 −φ 1L )(1 − φ12 L12 ) yt = C + at (1 −φ 1L )(1 − φ12 L12 ) yt = C + (1 − θ1L )(1 − θ12 L12 )at El primero se nota como AR(1)xSAR(1)12 El segundo como AR(1)xSAR(1)12 MA(1)xSMA(1)12 Correlograma (1) Considérese un modelo MA(1)xSMA(1)12. Por simplicidad se presenta sin constante: yt = (1 −θ 1L )(1 − θ12 L12 ) at yt = at −θ 1at −1 − θ12 at −12 + θ1θ12 at −13 Las covarianzas del proceso son: γ 1 = COV ( yt , yt −1 ) = E [( at −θ 1at −1 − θ12 at −12 + θ1θ12 at −13 )x x ( at −1 −θ 1at − 2 − θ12 at −13 + θ1θ12 at −14 ) ] = [ ] 2 2 2 = E −θ 1at2−1 − θ1θ12 at −13 = ( −θ1σ a2 )(1 + θ12 ) 11 Correlograma (2) γ 2 = COV ( yt , yt − 2 ) = E [( at −θ 1at −1 − θ12 at −12 + θ1θ12 at −13 )x x ( at − 2 −θ 1at − 3 − θ12 at −14 + θ1θ12 at −15 ) ] = 0 Y, de la misma forma, se deduce que γ3, γ4, ..., γ10 = 0 Las autocovarianzas 11, 12 y 13 serán no nulas, y γk = 0 con k>13. De esta forma, el correlograma tendrá valores no nulos para k=1, 11, 12 y 13. Correlograma (3) Suponiendo modelos MA de orden bajo, tanto para la parte ordinaria como para la parte estacional, el correlograma tendrá coeficientes no nulos para los primeros retardos (hasta el orden de la parte ordinaria) y en torno a la frecuencia estacional: en torno a 12 si es SMA(1)12, en torno a 12 y 24 si es SMA(2)12, etc. 12 Correlograma (4) Correlograma de SARMA (0,1)(0,1)12: yt = (1-0.3*L) (1-0.5*L12) at ============================================================== Included observations: 1000 ============================================================== Autocorrelation Partial Correlation AC PAC Q-Stat Prob ============================================================== **| | **| | 1-0.261-0.261 68.388 0.000 *| | *| | 2-0.061-0.139 72.171 0.000 .| | *| | 3-0.004-0.064 72.183 0.000 .| | .| | 4 0.047 0.022 74.420 0.000 .| | .| | 5-0.014 0.002 74.613 0.000 .| | .| | 6 0.020 0.028 75.034 0.000 .| | .| | 7-0.042-0.030 76.804 0.000 .| | .| | 8-0.017-0.039 77.111 0.000 .| | .| | 9 0.005-0.021 77.132 0.000 .| | .| | 10 0.035 0.025 78.389 0.000 .|* | .|* | 11 0.092 0.123 87.001 0.000 ***| | ***| | 12-0.395-0.363 245.35 0.000 .|* | *| | 13 0.113-0.090 258.41 0.000 .| | *| | 14 0.013-0.064 258.60 0.000 .| | .| | 15 0.034 0.014 259.80 0.000 ============================================================== Correlograma (5) Correlograma de SARMA (1,0)(1,0)12: (1-0.5*L) (1-0.7*L12)yt=at ============================================================== Included observations: 1000 ============================================================== Autocorrelation Partial Correlation AC PAC Q-Stat Prob ============================================================== .|*** | .|*** | 1 0.459 0.459 210.89 0.000 .|* | *| | 2 0.150-0.077 233.43 0.000 .|* | .| | 3 0.070 0.039 238.29 0.000 .|* | .|* | 4 0.102 0.081 248.75 0.000 .| | .| | 5 0.061-0.026 252.51 0.000 .|* | .|* | 6 0.099 0.098 262.42 0.000 .|* | .| | 7 0.070-0.018 267.31 0.000 .|* | .| | 8 0.078 0.052 273.42 0.000 .| | .| | 9 0.018-0.048 273.76 0.000 .|* | .|* | 10 0.072 0.089 279.06 0.000 .|** | .|** | 11 0.294 0.296 366.80 0.000 .|***** | .|***** | 12 0.690 0.599 850.04 0.000 .|*** | **| | 13 0.335-0.297 963.69 0.000 .|* | .| | 14 0.112 0.020 976.52 0.000 .| | .| | 15 0.048-0.038 978.82 0.000 .|* | .| | 16 0.074-0.011 984.47 0.000 .| | .| | 17 0.042 0.019 986.25 0.000 .|* | .| | 18 0.098 0.024 996.01 0.000 .|* | .| | 19 0.100 0.055 1006.2 0.000 .|* | .| | 20 0.080-0.022 1012.7 0.000 .| | .| | 21-0.012-0.032 1012.9 0.000 .| | .| | 22 0.021-0.001 1013.3 0.000 .|* | .| | 23 0.177-0.019 1045.4 0.000 .|**** | .| | 24 0.466 0.000 1268.1 0.000 .|** | .| | 25 0.239 0.005 1326.6 0.000 .|* | .| | 26 0.076-0.017 1332.6 0.000 .| | .| | 27 0.010-0.033 1332.7 0.000 .| | .| | 28 0.043 0.024 1334.5 0.000 .| | .| | 29 0.024 0.000 1335.1 0.000 .|* | .| | 30 0.073-0.029 1340.6 0.000 .|* | .| | 31 0.083-0.025 1347.7 0.000 .|* | .| | 32 0.069 0.021 1352.6 0.000 .| | .| | 33-0.033-0.022 1353.7 0.000 .| | .| | 34 0.000 0.040 1353.7 0.000 .|* | .| | 35 0.101-0.026 1364.4 0.000 .|** | .| | 36 0.305-0.010 1461.3 0.000 ============================================================== 13 Modelos no estacionarios (1) PIB trimestral Uruguay (logaritmo) 5,0 4,9 4,8 4,7 4,6 4,5 4,4 4,3 4,2 4,1 jun-08 jun-07 jun-06 jun-05 jun-04 jun-03 jun-02 jun-01 jun-00 jun-99 jun-98 jun-97 jun-96 jun-95 jun-94 jun-93 jun-92 jun-91 jun-90 jun-89 jun-88 jun-87 jun-86 jun-85 jun-84 jun-83 jun-82 jun-81 4,0 Modelos no estacionarios (2) Como puede observarse, la serie es claramente no estacionaria: presenta tendencia pero, como se comprobará a continuación, existen otros elementos que determinan la no estacionariedad de la serie. Veremos el gráfico de la primera diferencia de la serie (∆ log PIBt) y de la diferencia cuarta: ∆4 log PIBt = log (PIBt) – log(PIBt-4 ) 14 Modelos no estacionarios (3) ∆ log PIB 0,2 0,2 0,1 0,1 jun-08 jun-07 jun-06 jun-05 jun-04 jun-03 jun-02 jun-01 jun-00 jun-99 jun-98 jun-97 jun-96 jun-95 jun-94 jun-93 jun-92 jun-91 jun-90 jun-89 jun-88 jun-87 jun-86 jun-85 jun-84 jun-83 jun-82 jun-81 0,0 -0,1 -0,1 -0,2 -0,2 Modelos no estacionarios (4) Si bien la serie no parece presentar tendencia, se observa un “pico” regular en el cuarto trimestre de cada año, mientras que se produce un “valle” en el primer trimestre. Es decir, la media de la serie no es constante, sino sistemáticamente más alta en el cuarto trimestre, más baja en el primero, etc. 15 Modelos no estacionarios (5) ∆4 log PIB 0,2 0,2 0,1 0,1 jun-08 jun-07 jun-06 jun-05 jun-04 jun-03 jun-02 jun-01 jun-00 jun-99 jun-98 jun-97 jun-96 jun-95 jun-94 jun-93 jun-92 jun-91 jun-90 jun-89 jun-88 jun-87 jun-86 jun-85 jun-84 jun-83 jun-82 jun-81 0,0 -0,1 -0,1 -0,2 -0,2 -0,3 Modelos no estacionarios (6) Es posible que la aplicación de la diferencia estacional no sea suficiente para transformar en estacionaria a la serie. En el gráfico previo la serie resultante parece seguir un proceso del tipo de caminata al azar, aunque serían necesarios otros elementos de análisis (análisis del correlograma, por ejemplo) para concluir sobre la conveniencia de una diferencia adicional. A continuación el gráfico con ambas diferencias. 16 Modelos no estacionarios (7) ∆∆4 log PIB 0,2 0,1 0,1 jun-08 jun-07 jun-06 jun-05 jun-04 jun-03 jun-02 jun-01 jun-00 jun-99 jun-98 jun-97 jun-96 jun-95 jun-94 jun-93 jun-92 jun-91 jun-90 jun-89 jun-88 jun-87 jun-86 jun-85 jun-84 jun-83 jun-82 jun-81 0,0 -0,1 -0,1 -0,2 SARIMA - Notación ► Un proceso ARIMA(p,d,q) se plantea como: Φ(L) (L) (1(1-L)d(yt-µ) = Θ(L)at ► Un proceso SARIMA(p,d,q)(P,D,Q)s como: Φ(L) (L) φ(L)(1(L)(1-L)D(1(1-L)d (yt-µ) = Θ(L)θ (L)θ(L)at ►En el caso que el proceso incorpore otros componentes determiní (efectos determinísticos calendario, intervenciones por outliers, outliers, etc.): Φ(L) (L) φ(L)(1 (L)(1--L)D(1(1-L)d (yt-Σβj xjt) = Θ(L)θ (L)θ(L)at 17 El modelo de aerolíneas Al modelizar los totales mensuales de pasajeros en aerolíneas, Box y Jenkins en su libro Time Series Analysis (1976) desarrollaron un modelo de dos coeficientes en forma factorizada que hoy es conocido como “modelo de aerolíneas” (airline model). Para una serie de tiempo Zt con s ≥ 2 observaciones por año (por ejemplo, s = 4 para observaciones trimestrales), el modelo es: (1-L)(1-Ls) Zt = (1-θ L) (1- Θ Ls)εt donde L corresponde al operador de retardo (en muchos artículos aparece como B) y εt un ruido blanco gaussiano. Los parámetros cumplen -1≤θ, Θ≤1 y para series de tiempo económicas Θ≥0. El modelo de aerolíneas es por lejos el modelo más usado para series de tiempo económicas de frecuencia mensual y trimestral. AMB Sea un vector de observaciones y: y = ( yt1, ... ,ytm ) where 0< t1< … < tm, El programo TRAMO ajusta el modelo de regresión yt = zt´β+ xt donde β= vector de coef. de regresión z´t – matrix de variables de regresión xt – sigue un proceso estocástico ARIMA estacional (SARIMA): φ(L)δ(L)xt = θ(L)at donde L es el operador de retardos, at se supone una innovación ruido blanco n.i.i.d. (0,Va) 18 AMB El enfoque ARIMA Model Based (AMB) será abordado a partir del método de los programas TRAMO-SEATS. Sea un vector de observaciones y: y = ( yt1, ... ,ytm ) where 0< t1< … < tm, El programo TRAMO ajusta el modelo de regresión yt = zt´β+ xt donde β= vector de coef. de regresión z´t – matrix de variables de regresión xt – sigue un proceso estocástico ARIMA estacional (SARIMA): φ(L)δ(L)xt = θ(L)at donde L es el operador de retardos, at se supone una innovación ruido blanco n.i.i.d. (0,Va) AMB φ(L), δ(L),θ(L) son polinomios finitos en L que tienen la forma multiplicativa: δ(L)=(1-L)d(1 - Ls)D φ(L) = (1+φ1L+...+φPLP) (1+Φ1Βs) θ(L) = (1+θ1L+ … +θqLq) (1+Θ1Ls) donde “s” es el número de obs. por año (frecuencia). El programa SEATS descompone xt como: xt=pt+st+ct+ut donde pt , st , ct y ut son los componentes de Tend-Ciclo, Estacional, Transitorio e Irregular. 19 AMB El ajuste estacional corresponde al caso particular en que x t = nt + s t siendo nt la serie ajustada por estacionalidad. nt = pt + ct + ut Obsérvese que la serie ajustada por estacionalidad conserva el componente irregular. En el análisis de coyuntura es preferible trabajar con la estimación del componente de tendencia-ciclo. AMB Con el enfoque AMB se obtienen las raíces de los polinomios AR y se asignan a st o nt de acuerdo con su frecuencia (espectral) asociada. Es decir, de acuerdo con su valor. De esta forma δ(L) y φ(L) pueden ser factorizados como: δ(L) = δs(L) . δn(L) φ(L) = φs(L) . φn(L) Por ejemplo, si δ(L) = ∆ ∆12 = ∆2 S donde S = 1+L+ L2 +... +L11 contiene las raíces unitarias estacionales, entonces δs(L) = S y δn(L) = ∆2 20 AMB A partir de SEATS pueden derivarse modelos para los componentes no observados: φs(L)δs(L)st = θs(L)ast φn(L)δn(L)nt = θn(L)ant donde ast y ant son innovaciones incorrelacionadas. Los polinomios MA θs(L), θn(L) cumplen que θ(L) at = θs(L) φn(L) δn(L) ast + θn(L) φs(L) δs(L) ant lo que asegura la consistencia entre el modelo de la serie observada y los correspondientes a los componentes. Filtros Lineales El temprano reconocimiento que en una serie de tiempo los componentes (y en particular la estacionalidad) pueden modificar su patrón de comportamiento, condujo a desarrollar modelos más “flexibles” que los determinísticos originalmente utilizados. Un filtro lineal simplemente corresponde a una combinación lineal de las observaciones de la serie xt: yt = c−k1 xt −k1 + ... + c−1 xt −1 + c0 xt + c1 xt +1 + ... + ck 2 xt + k 2 (I) 21 Filtros Lineales Los pesos cj se definen de manera que la serie yt filtrada capture los componentes de interés. Asi, un filtro para la tendencia deberá capturar la variación asociada con la variación asociada con el movimiento de largo plazo de la serie. Un filtro diseñado de esa forma, con pesos a priori, es un filtro fijo ad-hoc, en el sentido que es independiente de la serie particular a la que es aplicado. Tanto el filtro Hodrick-Prescott (HP) como los correspondientes al X-11 pueden ser caracterizados como filtros fijos ad-hoc, aunque estrictamente los coeficientes no son constantes). Filtros Lineales Pese a algunas ventajas, como su sencillez, la aplicación de estos filtros mostró algunas limitaciones relevantes. Debido a su carácter fijo, pueden ser obtenidos resultados espurios, por lo que para algunas series el componente en cuestión puede quedar sub o sobre-estimado. Volviendo a la expresión (I), ésta puede plantearse como: yt = C ( B, F ) xt donde k1 k2 C ( B , F ) = ∑ c− j B + ∑ c j F j j j =1 j =1 B – operador de rezago (Bxt = xt-1) y F de adelanto (Fxt=xt+1) 22 Filtros Lineales Si k1=k2 y cj=c-j ∀j el filtro se denomina centrado y simétrico. El filtro se transforma en: k C ( B, F ) = c0 + ∑ c j ( B j + F j ) j =1 Si k1≠k2 o cj≠c-j ∀j el filtro será no centrado o asimétrico y su aplicación generará un efecto de fase en el resultado (la serie filtrada) en el sentido de que se produce una distorsión sistemática en la fecha de los eventos entre el input y el output (por ejemplo, en puntos de giro). Filtros Lineales Uno de los problemas que se presenta con los filtros centrados y simétricos es su aplicación en los extremos de la serie. Si una serie tiene T observaciones, cuando el filtro se aplica a la observación t, si T≥t+k no hay problema para su aplicación, pero si T<t+k el filtro no puede ser aplicado. El problema se presenta también al comienzo de la serie, pero el interés generalmente se encuentra en la extracción correcta de señales sobre el final de la serie. 23 Filtros Lineales El procedimiento X-11 (y el X-12) incorpora un conjunto de filtros asimétricos no-centrados para su aplicación en los extremos de la serie. Por otro lado, E. B. Dagum incorporó una extrapolación ARIMA (generando el X-11-ARIMA) para “aumentar” el tamaño de muestra y continuar utilizando los filtros centrados simétricos, principio que luego se recoge en el X-12-ARIMA. 24