a. sec(x + y) - Berkeley City College
Anuncio

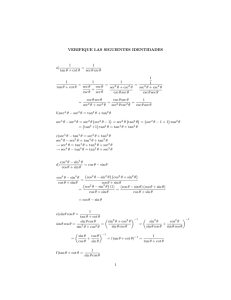
Verify the Identities: sec(x) sec(y) a. sec(x + y) = 1 − tan(x) tan(y) sin(x + y) = tan x + tan y cos x cos y cos(x − y) c. = tan x + cot y cos x sin y b. d. sin(x + y) sin(x − y) = cos2 y − cos2 x 1 − tan2 x 1 + tan2 x f. 1 + cos(2x) = cot x sin(2x) e. cos(2x) = g. sin(3x) = 3 sin x − 4 sin3 x 2 tan x h. sin(2x) = 1 + tan2 x i. 1 + tan x tan(2x) = tan(2x) cot(x) − 1 j. (cot x) − 1 1 − sin(2x) = (cot x) + 1 cos(2x) k. sin(4x) = 4 sin x cos x − 8 sin3 x cos x l. cos(4x) = 8 cos4 x − 8(cos2 x) + 1 2 m. sin(2x) = cot x + tan x 1 n. cos(2x) = 1 + tan(2x) tan x 2 tan x o. tan(2x) = 1 − tan2 x 2 tan x p. sin(2x) = 1 + tan2 x h i tan 21 (x + y) sin x + sin y h i q. = sin x − sin y tan 12 (x − y) r. 1 cos x cos y = tan x + tan y sin(x + y) s. (cot2 x + 1)(1 − cos2 x) = 1 t. (tan x + cot x)2 = sec2 x csc2 x