"apunte papirofléctico" de Ledesma
Anuncio

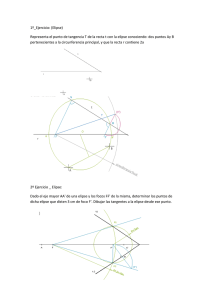
Apunte papirofléctico al Problema-107 del nº 22 de la Revista Escolar de la OIM Por Antonio Ledesma López. IES-1 de Requena. Valencia (España). He aquí el método que empleo en Papiroflexia Matemática para el: Trazado del pliegue tangente a una elipse (o una circunferencia) desde un punto P exterior a ella Q M B A L P C D N La geometría proyectiva nos da la idea, la misma para el dibujo y el plegado. 1: Trazar dos pliegues secantes a la elipse que pasen por P: se tendrán los puntos A, B, C y D de la elipse. Y hágase de forma que CA y DB no sean paralelos. 2: Los pliegues secantes CA y DB se cortan en Q. 3: Llamemos L a la intersección de los pliegues de las diagonales del cuadrilátero ABCD. 4: El pliegue QL da dos puntos en común con la elipse: M y N que son los puntos de tangencia pedidos. Apunte papirofléctico al Problema-107 del nº 22 de la Revista Escolar de la OIM Por Antonio Ledesma López. IES-1 de Requena. Valencia (España). El enunciado del Problema 107 es éste: Desde un punto exterior P a una elipse se trazan dos secantes, PAB y PCD (A, B, C y D son los puntos de intersección de las secantes con la elipse). Las rectas CA y DB se cortan en Q; desde Q se trazan las tangentes a la elipse QE y QF (E y F puntos de tangencia). Demostrar que P, E y F están alineados. De nuevo, trazando papiroflécticamente desde Q las tangentes a la elipse, obtenemos los puntos E y F. Q M B A F L E P C D N En ambos casos, los puntos de tangencia están alineados con L, el centro del cuadrilátero, y con los dos puntos de fuga, P y Q, respectivamente. Revista Escolar de la Olimpíada Iberoamericana de Matemática http://www.campus-oei.org/oim/revistaoim/ Edita: