grafos y matrices de adyacencia

Grafos. Matriz de adyacencia.
Grafo: Un grafo G es un conjunto de puntos o vértices unidos por aristas o arcos.
Ejemplo:
Matriz de adyacencia de un grafo: Dado un grafo G con n vértices, {v1, v2, …, vn}, su
matriz de adyacencia o matriz asociada es una matriz de dimensión nxn, donde cada elemento aij
es el número de aristas que unen los vértices vi y vj.
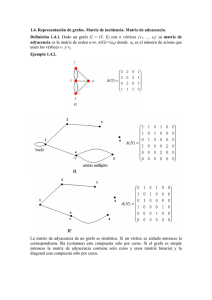
Ejemplo: La matriz de adyacencia del grafo del ejemplo anterior sería:
La matriz de adyacencia de un grafo es simétrica. Si un vértice es aislado entonces la
correspondiente fila (columna) está compuesta sólo por ceros.
Ejemplo:
Grafo dirigido o dígrafo: Un grafo dirigido o dígrafo es un grafo en el cual sus aristas tienen
una dirección definida y se representan por flechas.
Matriz de adyacencia de un grafo dirigido: Dado un grafo dirigido o dígrafo D, con n
vértices {v1, v2, …, vn} su matriz de adyacencia es una matriz de orden nxn, donde cada
elemento aij, es el número de aristas que tienen a vi como extremo inicial y a vj como extremo
final.
Ejemplo:
Las matrices de adyacencia de un grafo dirigido no tienen por qué ser simétricas.
Grafo ponderado: Es un grafo en el que cada arista tiene asignado un valor llamado
ponderación que puede interpretarse como el coste, la distancia… según el contexto.
Ejemplo:
En un grafo ponderado pueden plantearse diversos tipos de problemas, uno de ellos es encontrar
la distancia mínima entre dos vértices.
vértices. Con las distancias mínimas podemos construir una
matriz, la matriz de distancias mínimas,
mínimas en la que cada elemento aij representa la distancia
mínima para ir del vértice vi al vértice vj. Esta matriz es una matriz simétrica en la que cada
elemento de la diagonal principal es cero.
Ejemplo: La matriz de distancias mínimas del grafo anterior sería la siguiente:
Ejercicios:
1) Sean los grafos siguientes:
a) Escriba la matriz de adyacencia asociada a los grafos A y B de la figura anterior.
b) Si las matrices C y D unen los nodos numerados con las etiquetas 1, 2, 3, represente
los grafos asociados a dichas matrices de adyacencia.
2) En un instituto I hay alumnos de tres pueblos, A, B y C. La distancia entre A y B es 6
km, la de B a C es 7 km, la de A a C es 10 km y la de A a I es 8 km. Una empresa de
transporte escolar hace dos rutas: la ruta 1 parte de B y recorre sucesivamente C, A e I;
la ruta 2 parte de C y recorre sucesivamente B, A e I.
a) Determine la matriz M, 2x3, que expresa los kilómetros que recorren los alumnos de
cada pueblo por cada ruta.
b) El número de alumnos que siguen cada ruta de cada pueblo es:
Pueblo A: 10 alumnos la ruta 1 y 9 alumnos la ruta 2.
Pueblo B: 15 alumnos la ruta 1 y 8 alumnos la ruta 2.
Pueblo C: 5 alumnos la ruta 1 y 9 alumnos la ruta 2.
Determine la matriz N, 3x2, que indique los alumnos que siguen cada ruta de cada
pueblo.