Ejercicios Propuestos
Anuncio
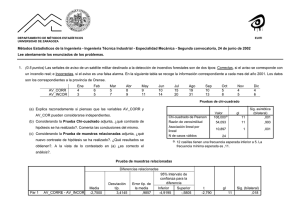
EJERCICIOS PROPUESTOS - COMPARACION DE MEDIAS 1. Para investigar si dos métodos de determinación de la concentración de protrombina en plasma difieren en sus resultados, se eligieron 8 sujetos y a cada uno se le sacó una muestra de sangre. Ambos métodos se aplicaron a parte de la misma muestra con los siguientes resultados: Sujeto 1 2 3 4 5 6 7 8 Método I 17 17 18 21 22 17 23 23 Método II 18 17 20 24 23 15 25 22 Haga la prueba de significación estadística. Cuál es su conclusión respecto a los métodos. 2. Se desea saber si existe diferencia de criterio entre dos profesores, respecto a la calificación de un examen escrito. Para eso se hace calificar a cada profesor, separadamente, los exámenes escritos de 14 alumnos. Las calificaciones aparecen en la tabla. Determine si existe diferente criterio entre los profesores para colocar la nota. Use nivel de significación 0,05. Alumno 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Profesor A 13 12 18 14 17 15 16 17 13 11 15 15 18 16 Profesor B 14 13 17 15 16 17 17 18 14 12 18 15 20 15 Compare sus resultados con la salida de SPSS: Estadísticos de muestras relacionadas Par 1 Profesor A Profesor B Media 15.00 15.79 N 14 14 Desviación típ. 2.184 2.190 Error típ. de la media .584 .585 Prueba de muestras relacionadas Par 1 Profesor A - Profesor B 3. Media Desviación típ. Error típ. de la media -.79 1.188 .318 t gl Sig. (bila teral ) 2.474 13 .028 Setenta pacientes que sufren epilepsia se dividieron al azar en dos grupos iguales. El grupo A recibió un tratamiento que incluía dosis diarias de vitamina D. El grupo B recibió el mismo tratamiento con la excepción de que a este grupo se le dio un placebo en lugar de vitamina D. El número medio de ataques convulsivos observados durante el periodo de tratamiento en los dos grupos fue de: x1 = 15,0 y x2 = 24,0 . Las varianzas de las muestras fueron: s A2 = 8,0 y sB2 = 12,0 . ¿Estos datos proporcionan evidencia suficiente para indicar que la vitamina D es efectiva para disminuir el número de ataques convulsivos? Sea α=0,05 4. Varios investigadores desean saber si es posible concluir que dos poblaciones de niños difieren respecto a la edad promedio en la cual pueden caminar por sí solos. Los investigadores obtuvieron los siguientes datos (edades en meses). Muestra en la población A: 9,5 10,5 9,0 9,75 Muestra en la población B: 12,5 9,5 13,5 13,75 10,0 13,0 12,0 13,75 10,0 13,5 10,0 12,5 9,5 12,0 9,5 10,0 9,75 13,5 12,0 12,0 ¿Qué pueden concluir los investigadores? Se dan dos dietas distintas a dos grupos de cerdos asignados aleatoriamente a esas dietas. Las ganancias en peso en determinado tiempo se anotan a continuación: Dieta A: 31 34 29 26 32 35 38 34 30 29 32 31 Dieta B: 26 24 28 29 30 29 32 26 31 29 32 28 a) Obtenga conclusiones tentativas a partir del diagrama de caja para las dos muestras. 40 38 36 34 32 30 Ganancia de peso 5. 28 26 24 22 N= 12 12 A B Dieta b) Determine si la ganancia de peso con dieta A difiere significativamente de la ganancia de peso con dieta B. Use la salida SPSS: Estadísticos de grupo Ganancia de peso Dieta A B N 12 12 Media 31.75 28.67 Desviación típ. 3.194 2.462 Error típ. de la media .922 .711 Prueba de muestras independientes Prueba de Levene para la igualdad de varianzas F Ganancia de peso Se han asumido varianzas iguales No se han asumido varianzas iguales .557 Sig. .463 Prueba T para la igualdad de medias t gl Sig. (bilateral) Diferencia de medias Error típ. de la diferencia 95% Intervalo de confianza para la diferencia Inferior Superior 2.648 22 .015 3.08 1.164 .669 5.498 2.648 20.659 .015 3.08 1.164 .660 5.507 6. Se estudia el efecto de un cierto estímulo sobre la presión sistólica de 12 individuos. Los datos aparecen en la tabla. Con un nivel de significación de 5% determine si la presión sistólica experimenta un cambio estadísticamente significativo con el estímulo aplicado. Individuo 1 2 3 4 5 6 7 8 9 10 11 12 7. Presión sistólica en mm Antes(A) Después(D) 120 124 130 118 140 128 140 135 126 130 126 127 128 131 131 127 132 125 141 137 118 132 129 135 Un investigador quiere determinar si la posición del paciente (A=sentado o B=acostado) afecta la medición de la presión arterial. El investigador decide usar cada paciente como su control y les toma la presión a 10 pacientes en ambas posiciones. Al analizar los resultados se obtienen los siguientes valores: Formule la hipótesis de nulidad y alternativa para las siguientes preguntas: a) Determine si la posición afecta la medición de la presión arterial utilizando la prueba adecuada al diseño del experimento. b) ¿Cuál habría sido la conclusión si el investigador hubiera realizado la prueba con 10 individuos diferentes para la posición A=sentado y 10 para la posición B=acostado? (con los mismos datos) c) ¿Señale ventajas del diseño de muestras pareadas en esta investigación? Revisar ejercicios de: Capítulo 9 de Milton, S. (2001) Estadística para Biología y ciencias de la salud 3ta edición. McGraw Hill Capítulo 11 de Pagano, M. Gauvreau, K. (2001) Fundamentos de Bioestadística. Thomson Learning.