α β γ
Anuncio

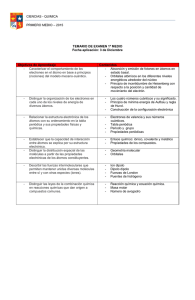
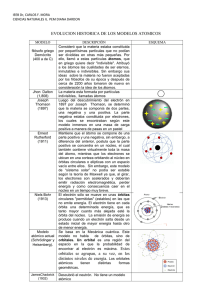
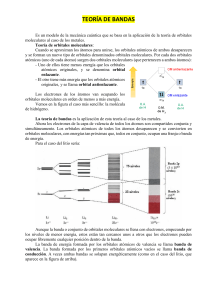
El método de Huckel extendido, propuesto por R. Hoffmann, es una extensión del método de Huckel que permite determinar de manera simultánea los orbitales moleculares σ y π. En éste método, las integrales hµµ , hµν y Sµν son parámetros que toman en cuenta la distancia entre los àtomos y la orientación relativa de los orbitales atómicos. Ejemplo. Estudio de la estructura electrónica del cluster Li4 Se generalizan las aproximaciones de Huckel a los orbitales 2s del àtomo de Li. Ponemos α = 2s Li h 2s Li energía del electrón 2s del Li; h es el operador hamiltoniano efectivo monoelectrónico. Se desprecia las integrales de recubrimiento entre los OA 2s. denotamos γ i j = 2s Li ,i h 2s Li , j = kβ k es un número comprendido entre 0 y 1 y depende de la distancia entre los átomos i y j. Si dos átomos son vecinos k=1. k disminuye a medida que se alejan los átomos. Analizar las estructuras plana cuadrada y tetraédrica para los clusters. Hay que encontrar los ceros del determinante: α −e β β γ β α −e γ β β γ γ β α −e β β α −e para la forma cuadrada γ = kβ (0≤ k ≤ 1) y para la tetraédrica γ = β (k=1). Hacemos m = - (α - e)/β y obtenemos: m4 – m2 (4 + 2k2 ) + 8k – 4k2 + k4 = 0 Cuyas soluciones son m1 = 2+k; m2 = - k; m3 = -2 + k y las energías de los OM son: e1 = α + 2 β + γ e2 = α − γ (nivel doblemente denerado) e3 = α − 2 β + γ